2.6   Introduciremos agora un concepto de grande interese na relación entre converxencia e topoloxía, que nos permitirá caracterizar os conxuntos pechados utilizando converxencia.

Definición.- Chámase punto de acumulación dun conxunto E a un punto x tal que para todo r>0 se cumpre

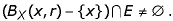
O conxunto de puntos de acumulación de E denomínase conxunto derivado, e se denota por E'. A razón do nome é que, para que teña sentido a noción de derivada dunha aplicación nun punto do seu dominio, éste debe ser de acumulación.

Lema.- Sexa x un punto de acumulación dun conxunto E. Entón toda bóla de centro x contén unha infinidade de puntos de E.