Derivada covariante e xeodésicas
Derivada covariante
Sexa $S$ unha superficie regular e $\alpha\colon I\to S$ unha curva diferenciable. Sexa $V\colon I\to\R^3$ un campo de vectores tanxente a $S$ ó longo de $\alpha$. Recordemos que isto quere dicir que $V(t)\in T_{\alpha(t)}S$ para todo $t\in S$.
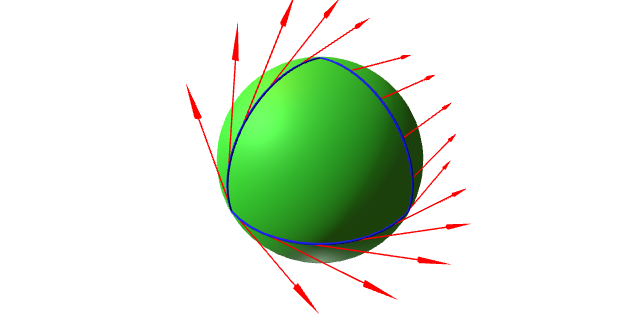
Se $\alpha\colon I\to S$ é unha curva parametrizada por arco nunha superficie orientada, vimos cando falamos da estructura complexa que $(\alpha', J\alpha')$ constitúe unha base ortonormal positivamente orientada ó longo da curva $\alpha$.
Non obstante, nótese que $\alpha''$ non é en xeral tanxente a $S$ ó longo de $\alpha$.
Defínese a derivada covariante de $V$ como o campo de vectores tanxente ó longo de $\alpha$, $\frac{D}{dt}V$ dado por \[ \frac{D}{dt}V(t)\equiv\frac{D V}{dt}(t)=V'(t)^\top =\left(\frac{dV}{dt}\right)^\top, \] onde $(\,\cdot\,)^\top$ denota a proxección no tanxente á superficie.
Equivalentemente, \[ \frac{DV}{dt}=V'-\langle V',\mathbf{N}\circ\alpha\rangle(\mathbf{N}\circ\alpha). \]
Pódese por tanto pensar en $\frac{D}{dt}$ como un operador que leva campos de vectores tanxentes ó longo de $\alpha$ en campos de vectores tanxentes ó longo de $\alpha$.
Sexa $S$ unha superficie regular e $\alpha\colon I\to S$ unha curva. Sexan $V$ e $W$ campos de vectores tanxentes a $S$ ó longo de $\alpha$. Entón, a derivada covariante satisfai:
- $\R$-linearidade: \[ \frac{D}{dt}(\lambda V+\mu W)=\lambda\frac{D}{dt}V+\mu\frac{D}{dt}W, \] para todo $\lambda,\mu\in\R$.
- Regra de Lebnitz: \[ \frac{D}{dt}(fV)=\frac{df}{dt}V+f\frac{D}{dt}V, \] para toda función diferenciable $f\colon I\to\R$.
- Compatibilidade coa primeira forma fundamental: \[ \frac{d}{dt}\langle V,W\rangle =\langle\frac{D}{dt}V,W\rangle+\langle V,\frac{D}{dt}W\rangle. \]
Recordémo-la definición dos símbolos de Christoffel \[ \mathbf{x}_{ij} =\sum_k \Gamma_{ij}^k\mathbf{x}_k + L_{ij}(\mathbf{N}\circ\mathbf{x}). \] Poñamos $\alpha(t)=\mathbf{x}(u(t))$, con $u(t)=(u^1(t), u^2(t))$ e $V(t)=\sum_i V^i(t)\,\mathbf{x}_i(u(t))$. Entón \[ \frac{DV}{dt}= \sum_k\left(\frac{dV^k}{dt} +\sum_{i,j}V^i\frac{du^j}{dt}(\Gamma_{ij}^k\circ u)\right) (\mathbf{x}_k\circ u). \]
A derivada covariante dunha superficie $S$ depende só da primeira forma fundamental de $S$.
Isto é consecuencia da fórmula anterior e do feito de que os símbolos de Christoffel só dependen da primeira forma fundamental.
Sexa $f\colon S_1\to S_2$ unha isometría entre superficies, $\alpha\colon I\to S_1$ unha curva, e $V\colon I\to\R^3$ un campo de vectores ó longo de $\alpha$. Denotemos por $\frac{{}^1D}{dt}$ á derivada covariante en $S_1$ ó longo de $\alpha$, e por $\frac{{}^2D}{dt}$ á derivada covariante de $S_2$ ó longo de $f\circ\alpha$. Entón, \[ df_{\alpha(t)}\Bigl(\frac{{}^1D}{dt}V\Bigr)(t) =\frac{{}^2D}{dt}\bigl(df(V)\bigr)(t), \] sendo $df(V)$ o campo de vectores ó longo de $f\circ\alpha$ definido mediante $df(V)(t)=df_{\alpha(t)}(V(t))$.
A derivada covariante é unha cuestión local, así que chega con ve-lo resultado nunha veciñanza coordenada. Sexa $\mathbf{x}\colon U\subset\R^2\to S_1$ unha parametrización arredor de $\alpha(t)$. Como $f$ é un difeomorfismo, $f\circ\mathbf{x}$ é unha parametrización de $S_2$ en $f(\alpha(t))$.
Escribimos $\alpha(t)=\mathbf{x}(u(t))$, $u(t)=(u_1(t),u_2(t))$, e $V(t)=\sum_i V^i(t)\mathbf{x}_i(u(t))$. Entón, $(f\circ\alpha)(t)=(f\circ\mathbf{x})(u(t))$, e pola regra da cadea, \[ \begin{aligned} \frac{d(f\circ\alpha)}{dt} &{}=\sum_i \frac{du^i}{dt}(f\circ\mathbf{x})_i,\\[1ex] df_{\alpha(t)}(V(t)) &{}=\sum_i V^i(t)df_{\mathbf{x}(u(t))}\mathbf{x}_i(u(t))\\ &{}=\sum_i V^i(t)(f\circ\mathbf{x})_i(u(t)). \end{aligned} \]
Como $f$ é unha isometría, os coeficientes da primeira forma fundamental de $S_1$ na parametrización $\mathbf{x}$, ${}^1g_{ij}$, coinciden cos coeficientes da primeira forma fundamental de $S_2$ na parametrización $f\circ\mathbf{x}$, ${}^2g_{ij}$, xa que \[ \begin{aligned} {}^2g_{ij} &{}=\langle(f\circ\mathbf{x})_i,(f\circ\mathbf{x})_j\rangle\\ &{}=\langle(df\circ\mathbf{x})(\mathbf{x}_i),(df\circ\mathbf{x})(\mathbf{x}_j)\rangle\\ &{}=\langle\mathbf{x}_i,\mathbf{x}_j\rangle ={}^1g_{ij}. \end{aligned} \]
Como os símbolos de Christoffel dependen só dos coeficientes da primeira forma fundamental, obtemos ${}^1\Gamma_{ij}^k={}^2\Gamma_{ij}^k$, tomando a notación coherente coa anterior.
Por tanto, tendo en conta a expresión en coordenadas da derivada covariante, \[ \begin{aligned} df\Bigl(\frac{{}^1D}{dt}V\Bigr) &{}=df\left(\sum_k\Bigl(\frac{dV^k}{dt} +\sum_{i,j}V^i\frac{du^j}{dt}({}^1\Gamma_{ij}^k\circ u)\Bigr) (\mathbf{x}_k\circ u)\right)\\ &{}=\sum_k\Bigl(\frac{dV^k}{dt} +\sum_{i,j}V^i\frac{du^j}{dt}({}^1\Gamma_{ij}^k\circ u)\Bigr) df(\mathbf{x}_k\circ u)\\ &{}=\sum_k\Bigl(\frac{dV^k}{dt} +\sum_{i,j}V^i\frac{du^j}{dt}({}^2\Gamma_{ij}^k\circ u)\Bigr) \bigl((f\circ\mathbf{x})_k\circ u\bigr)\\ &{}=\frac{{}^2D}{dt}\bigl(df(V)\bigr), \end{aligned} \] como queriamos probar.
Dito dun xeito máis resumido: as isometrías conmutan coa derivada covariante, \[ df\Bigl(\frac{{}^1D}{dt}\Bigr)=\frac{{}^2D}{dt}\bigl(df\bigr). \]
Un campo de vectores $V$ ó longo de $\alpha$ dise paralelo se $\frac{D}{dt}V=0$ en tódolos puntos.
Se $\alpha$ é unha curva regular, ser paralelo non depende da parametrización de $\alpha$.
Sexa $S$ un plano en $\R^3$ a $\alpha\colon I\to S$ unha curva no plano. Sexa $V$ un campo ó longo de $\alpha$. Como o vector normal unitario de $S$ é constante $N_{\alpha(t)}=N$ temos que $\langle V,N\rangle=0$ implica \[ 0=\frac{d}{dt}\langle V,N\rangle =\langle \frac{dV}{dt},N\rangle, \] así que $\frac{DV}{dt}=\frac{dV}{dt}$. Por tanto, $V$ é paralelo se e só se $V$ é constante.
Sexan $V$ e $W$ campos paralelos ó longo dunha curva $\alpha$. Entón:
- $aV+bW$ é paralelo ó longo de $\alpha$ para calquera $a,b\in\R$.
- $\langle V,W\rangle$ é constante ó longo de $\alpha$.
Isto é consecuencia inmediata das propiedades da derivada covariante.

Sexa $S$ unha superficie orientable con estructura complexa $J$. Sexa $\alpha\colon I\to S$ unha curva en $S$. Entón, \[ \frac{D}{dt}J=J\frac{D}{dt}. \]
Sexa $S$ unha superficie orientable con estructura complexa $J$. Sexa $\alpha\colon I\to S$ unha curva en $S$. Se $V$ é paralelo ó longo de $\alpha$, entón tamén o é $JV$.
Xeodésicas
Sexa $S$ unha superficie regular.
Unha curva $\gamma\colon I\to S$ dise unha xeodésica se $\frac{D}{dt}\gamma'=0$.
Dito doutro xeito, unha curva é xeodésica se o seu vector tanxente é paralelo ó longo da propia curva.
A propiedade de ser xeodésica depende da parametrización. Por exemplo, $\gamma(t)=(t,0,0)$, é unha xeodésica no plano $z=0$, pero a curva $\sigma(t)=(t^3,0,0)$ ten a mesma traza ca $\gamma$ e non é xeodésica, xa que $\frac{D}{dt}\sigma'(t)=\sigma''(t)=(6t,0,0)\neq(0,0,0)$.
É común referirse a unha curva como xeodésica cando pode ser reparametrizada para ser unha xeodésica. Cando queiramos ser estrictos coa terminoloxía, a este tipo de curvas chamarémolas prexeodésicas. Non obstante, en moitos casos seremos menos precisos e tamén chamaremos xeodésica a unha curva que cando se reparametriza proporcionalmente ó arco é unha xeodésica no sentido da definición anterior.
As xeodésicas nunha superficie poden entenderse como as traxectorias inerciais dentro desa superficie, é dicir, como o movemento dunha partícula que só está suxeita ás forzas de ligadura da superficie (aquelas que obrigan á partícula a estar na superficie).
Sexa $\gamma$ unha xeodésica nunha superficie $S$. Entón, $\lVert\gamma'\rVert$ é constante.
Sexa $\gamma$ unha xeodésica. Entón, \[ \frac{d}{dt}\langle\gamma',\gamma'\rangle =2\langle\frac{D}{dt}\gamma',\gamma'\rangle=0, \] o que implica que $\langle\gamma',\gamma'\rangle$ é constante.
Sexa $\gamma\colon I \to S$ unha xeodésica non constante. Sexa $h\colon J\to I$ un difeomorfismo de intervalos de $\R$, e $\beta=\gamma\circ h$ a correspondente reparametrización de $\gamma$. Entón, $\beta$ é xeodésica se e só se $h$ é unha función afín.
As xeodésicas no plano son as rectas parametrizadas con velocidade constante.
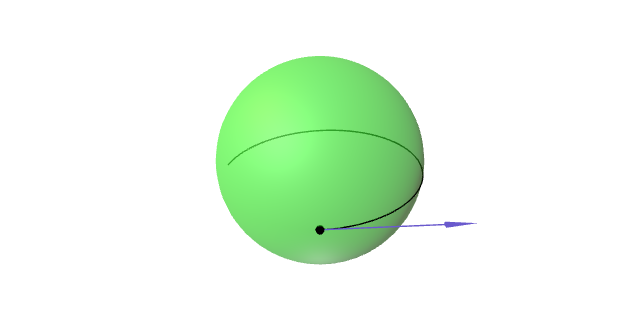
As xeodésicas na esfera son círculos máximos parametrizados proporcionalmente ó arco. Máis concretamente, a xeodésica maximal $\gamma\colon\R\to\mathbb{S}^2(r)$ tal que $\gamma(0)=p\in\mathbb{S}^2(r)$ e $\gamma'(0)=v\in T_p\mathbb{S}^2(r)$ pode parametrizarse como \[ \gamma(t) =\cos\Bigl(\frac{\lVert v\rVert}{r}t\Bigr)\,p +\frac{r}{\lVert v\rVert}\sin\Bigl(\frac{\lVert v\rVert}{r}t\Bigr)\,v. \]
Se $\mathbf{x}$ é unha parametrización, e $\gamma$ está contida na súa imaxe, entón escribindo $\gamma(t)=\mathbf{x}(u(t))$ con $u(t)=(u^1(t),u^2(t))$ temos que $\gamma$ é xeodésica se e só se satisfai a ecuación diferencial \[ \frac{d^2u^k}{dt^2} +\sum_{i,j}\frac{du^i}{dt}\frac{du^j}{dt}(\Gamma_{ij}^k\circ u)=0, \] con $k=1,2$.
Sexa $S$ unha superficie regular, $p\in S$ e $v\in T_p S$. Entón existe unha única xeodésica $\gamma_v\colon I_v\to S$ tal que
- $I_v$ é un intervalo aberto.
- $0\in I_v$, $\gamma_v(0)=p$, $\gamma_v'(0)=v$.
- Se $\sigma\colon J\to S$ é outra xeodésica con $\sigma(0)=p$, $\sigma'(0)=v$, entón $J\subset I_v$ e $\sigma_{\vert J}=\gamma_{v\vert J}$.
Dúas xeodésicas dunha superficie poden intersecarse, por exemplo, como sucede na esfera. O conxunto de definición dunha xeodésica non ten por que ser todo $\R$.
Unha superficie regular $S$ dise xeodésicamente completa se toda xeodésica maximal desa superficie está definida en todo $\R$.
Sexa $f\colon S_1\to S_2$ é unha isometría entre superficies, e $\gamma\colon I\to S_1$ unha xeodésica. Entón $f\circ\gamma$ é unha xeodésica en $S_2$.
Denotemos por $\frac{{}^1D}{dt}$ á derivada covariante de $S_1$ ó longo de $\gamma$, e por $\frac{{}^2D}{dt}$ á derivada covariante de $S_2$ ó longo de $f\circ\gamma$. Como a derivada covariante e as isometrías conmutan, e $\gamma$ é unha xeodésica de $S_1$, temos \[ \begin{aligned} \frac{{}^2D}{dt}(f\circ\gamma)' &{}=\frac{{}^2D}{dt}\bigl(df(\gamma')\bigr)\\ &{}=df\Bigl(\frac{{}^1D}{dt}\gamma'\Bigr)=0, \end{aligned} \] co que $f\circ\gamma$ é xeodésica de $S_2$.
As xeodésicas do cilindro $\mathbb{S}^1\times\R$ correspóndense con hélices circulares, rectas verticais, ou circunferencias horizontais.
Para calcular estas xeodésicas observámo-lo feito de que o cilindro é localmente isométrico ó plano. De feito, o cilindro pode deformarse isometricament nun plano mediante a homotopía por isometrías $\mathbf{x}\colon[0,1]\times\R^2\to\R^3$ dada por \[ \mathbf{x}_t(u,v)=\left( \frac{1 + t}{1 - t}\,\sin\Bigl(\frac{1 - t}{1 + t}u\Bigr),\, \frac{1 + t}{1 - t}\Bigl(1 - \cos\Bigl(\frac{1 - t}{1 + t}u\Bigr)\Bigr) - 1,\, v \right). \]
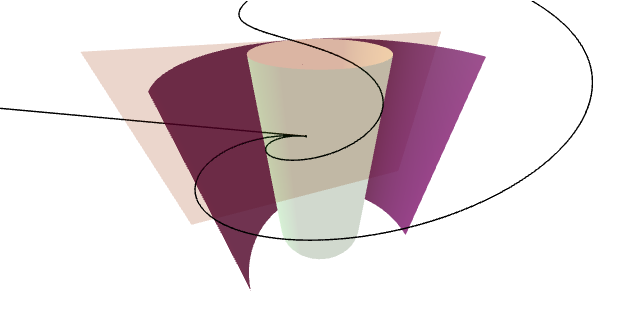
Probar que dous puntos distintos da recta rexeneratriz dun cilindro poden ser unidos por un número infinito de xeodésicas.
Curvatura xeodésica
Supoñamos que $S$ é unha superficie regular orientada e que $\mathbf{N}$ é un vector normal unitario orientado positivamente.
Sexa $\alpha\colon I\to S$ unha curva parametrizada polo parámetro lonxitude de arco. Entón $(\alpha'(s),J\alpha'(s),\mathbf{N}_{\alpha(s)})$ é unha base ortonormal positivamente orientada de $\R^3$ chamada triedro de Darboux.
Defínese a curvatura xeodésica de $\alpha$, $\kappa_g[\alpha]\equiv\kappa_g$, como \[ \kappa_g(s)=\langle\alpha''(s),J\alpha'(s)\rangle =\kappa(s)\langle\mathbf{n}(s),J\mathbf{t}(s)\rangle. \]
Por outro lado, a curvatura normal de $\alpha$, $\kappa_n[\alpha]=\kappa_n$, é \[ \begin{aligned} \kappa_n(s) &{}=\langle A_{\alpha(s)}(\alpha'(s)),\alpha'(s)\rangle\\ &{}=\langle\alpha''(s),\mathbf{N}_{\alpha(s)}\rangle\\ &{}=\kappa(s)\langle\mathbf{n}(s),\mathbf{N}_{\alpha(s)}\rangle. \end{aligned} \]
Así, para unha curva parametrizada por arco \[ \alpha''=\kappa_g\, J\alpha'+\kappa_n\,(\textbf{N}\circ\alpha). \]
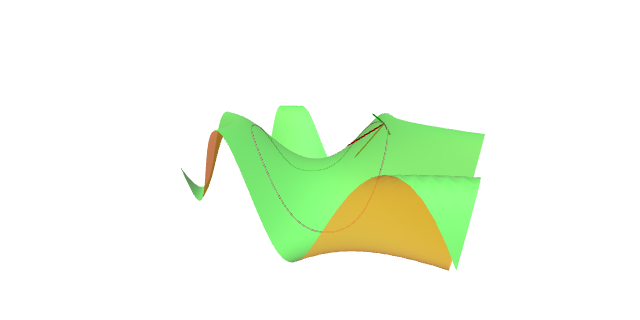
No seguinte gráfico presentase a curvatura dunha curva, que ó estar contida nunha superficie se descompón como a súa compoñente tanxente (a curvatura xeodésica) e a súa compoñente normal (a curvatura normal). Desde o punto de vista da mecánica dunha partícula que se move dentro dunha superficie, a curvatura xeodésica expresa a súa aceleración normal dentro do medio no que está, mentres que a curvatura normal expresa as chamadas forzas de ligadura que fan que a partícula estea confinada a esa superficie.

Supoñamos agora que a curva $\alpha$ non está parametrizada por arco. Tomámo-lo parámetro lonxitude de arco $g(t)=\int_{t_0}^t\lVert\alpha'(u)\rVert\,du$. Definímo-las curvaturas xeodésica e normal de $\alpha$ como as curvaturas xeodésicas e normal da súa parametrización por arco en puntos correspondentes, é dicir, se $\beta(s)=\alpha(g^{-1}(s))$ entón \[ \begin{aligned} \kappa_g[\alpha](t) & {}=\kappa_g[\beta](g(t)),\\[1ex] \kappa_n[\alpha](t) & {}=\kappa_n[\beta](g(t)). \end{aligned} \]
Sexa $S$ unha superficie orientada, con vector normal $N$, e $\alpha\colon I\to S$ unha curva. Entón as súas curvaturas xeodésica e normal poden ser expresadas como \[ \begin{aligned} \kappa_g &{}=\frac{\det(\alpha',\alpha'',\mathbf{N}\circ\alpha)}{\lVert\alpha'\rVert^3},\\ \kappa_n &{}=\frac{\langle\alpha'',\mathbf{N}\circ\alpha\rangle}{\lVert\alpha'\rVert^2}. \end{aligned} \]
A curvatura xeodésica cambia de signo se invertímo-la orientación da curva. En efecto, se $\alpha\colon[a,b]\to S$ é unha curva regular e tomámo-la curva coa orientación inverida $\beta\colon[a,b]\to S$, $t\mapsto\beta(t)=\alpha(a+b-t)$, entón obtemos $\kappa_g[\alpha](t)=-\kappa_g[\beta](a+b-t)$.
Sexa $\gamma\colon I\to S$ unha curva nunha superficie regular $S$. Entón $\gamma$ ten curvatura xeodésica nula, $\kappa_g=0$, se e só se a súa reparamentrización por arco é un xeodésica.
Sexa $s(t)$ o parámetro lonxitude de arco e $\beta$ a reparametrización por arco de $\gamma$. Recordemos que por definición $\kappa_g[\beta](s(t))=\kappa_g[\gamma](t)$, é dicir, que a curvatura xeodésica coincide en puntos correspondentes.
Recordemos ademais, que por estar $\beta$ parametrizada por arco, temos $\beta''=\kappa_g[\beta]\, J\beta+\kappa_n[\beta]\, (\mathbf{N}\circ\beta)$. Por tanto, \[ \frac{D\beta'}{dt}=\kappa_g[\beta]\, J\beta. \] Entón, $\beta$ é xeodésica se e só se $\kappa_g[\beta]=0$, se e só se $\kappa_g[\gamma]=0$.
Unha curva é xeodésica se e só se está parametrizada proporcionalmente ó arco e a súa curvatura xeodésica é cero.
Este resultado séguese da proposición anterior, pero faremos unha demostración alternativa empregando a fórmula da curvatura xeodésica para unha curva regular arbitraria.
Supoñamos que $\gamma\colon I\to S$ é unha xeodésica. Xa vimos que $\gamma$ está parametrizada proporcionalmente ó arco. Descompoñendo $\gamma''$ na súa parte tanxente e normal obtemos \[ \begin{aligned} \gamma'' &{}=\frac{D\gamma'}{dt} +\langle\gamma'',\mathbf{N}\circ\gamma\rangle(\mathbf{N}\circ\gamma)\\ &{}=\langle\gamma'',\mathbf{N}\circ\gamma\rangle(\mathbf{N}\circ\gamma). \end{aligned} \] Por tanto, \[ \det(\gamma',\gamma'',\mathbf{N}\circ\gamma) =\langle\gamma'',\mathbf{N}\circ\gamma\rangle \det(\gamma',\mathbf{N}\circ\gamma,\mathbf{N}\circ\gamma)=0, \] o que implica $\kappa_g[\gamma]=0$.
Reciprocamente, supoñamos que $\langle\gamma',\gamma'\rangle=c\in\R$ e que $\kappa_g[\gamma]=0$. Como $\kappa_g[\gamma]=0$ temos que $\det(\gamma',\gamma'',\mathbf{N}\circ\gamma)=0$. Por tanto, $\gamma''$ depende linearmente de $\gamma'$ e $\mathbf{N}\circ\gamma$. Entón, podemos escribir \[ \gamma'' =\frac{1}{c}\langle\gamma'',\gamma'\rangle\gamma' +\langle\gamma'',\mathbf{N}\circ\gamma\rangle(\mathbf{N}\circ\gamma). \] Agora ben, $\langle\gamma',\gamma'\rangle=c$ implica que, derivando, $2\langle\gamma'',\gamma'\rangle=0$. Por tanto, $\gamma'' =\langle\gamma'',\mathbf{N}\circ\gamma\rangle(\mathbf{N}\circ\gamma)$, e en consecuencia, $\frac{D\gamma'}{dt}=0$.
Considerámo-la curva xeneratriz $\sigma(s)=(y(s),z(s))$, $y>0$, parametrizada por arco. A superficie de revolución xerada por esa curva pode parametrizarse como $\mathbf{x}(s,\theta)=(y(s)\cos\theta,y(s)\sin\theta,z(s))$. Entón:
- Os meridianos dunha superficie de revolución son xeodésicas.
- Un paralelo dunha superficie de revolución é unha xeodésica se e só se o vector tanxente á curva xeneratriz nese punto é vertical.
Considerámo-lo cono recto parametrizado como $\mathbf{x}(u,v)=(v\cos u, v\sin u, v)$, $v>0$. O cono é localmente isométrico a un plano; esta isometría consiste en desenvolve-lo cono ata transformalo nun sector circular. Por tanto, as xeodésicas do cono consisten en compoñe-las rectas dese sector circular coa isometría local.
Podemos deformar o cono nun aberto de plano mediante unha homotopía por isometrías $\mathbf{x}\colon[0,\pi/4]\times\R\times(0,\infty)\to\R^3$ definida como $\mathbf{x}_t=(x_t,y_t,z_t)$, onde \[ \begin{aligned} x_t(u,v)&{}= v\, \bigl(\cos t + \sin t\bigr) \cos\Bigl(\frac{u}{\cos t + \sin t}\Bigr),\\ y_t(u,v)&{}= v\, \bigl(\cos t + \sin t\bigr) \sin\Bigl(\frac{u}{\cos t + \sin t}\Bigr),\\[1ex] z_t(u,v)&{}= v \bigl(\cos t - \sin t\bigr). \end{aligned} \]

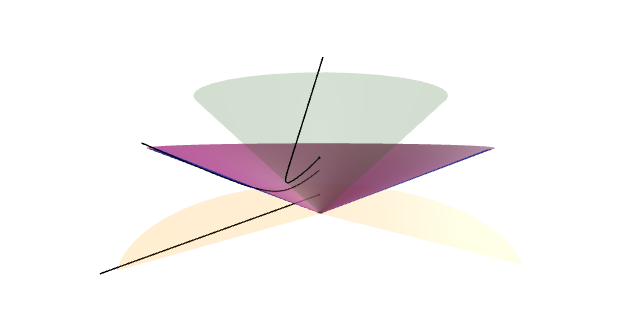
Transporte paralelo
O transporte paralelo danos un xeito de move-la xeometría local dunha superficie ó longo dunha curva. De feito, a especificación do transporte paralelo é equivalente a dar unha derivada covariante. En xeometría diferencial máis avanzada, a derivada covariante vese como unha versión infinitesimal do transporte paralelo, e efectivamente, ás veces é convinte especifica-lo transporte paralelo en vez da derivada covariante.
Ademais de estar intimamente relacionado coa derivada covariante, o transporte paralelo tamén está vinculado coa curvatura a través dun concepto denominado holonomía. Neste curso non trataremos esta última, pero daremos unha pequena idea do que quere dicir.
Sexa $\alpha\colon I\to S$ unha curva nunha superficie regular $S$. Sexa $t_0\in I$ e $v\in T_{\alpha(t_0)}S$. Entón existe un único campo de vectores paralelo $V$ ó longo de $\alpha$ tal que $V(t_0)=v$.
Supoñamos primeiro que $\alpha$ está contida nunha veciñanza coordenada $\mathbf{x}\colon U\subset\R^2\to S$, e poñamos $\alpha(t)=\mathbf{x}(u(t))$, $u(t)=(u^1(t), u^2(t))$, $V(t)=\sum_i V^i(t)\,\mathbf{x}_i(u(t))$, $v=\sum_i v^i\mathbf{x}_i(u(t_0))$. Entón, vimos que \[ \frac{DV}{dt}= \sum_k\left(\frac{dV^k}{dt} +\sum_{i,j}V^i\frac{du^j}{dt}(\Gamma_{ij}^k\circ u)\right) (\mathbf{x}_k\circ u). \] Por tanto, $V$ é paralelo se e só se \[ \begin{aligned} \frac{dV^k}{dt} &{}=-\sum_{i,j}V^i\frac{du^j}{dt}(\Gamma_{ij}^k\circ u),\\ V^k(t_0) &{}=v^k, \qquad k=1,2. \end{aligned} \] Este é un problema de valor inicial linear, co que ten solución única en todo o conxunto de definición.
Supoñamos agora que $\alpha(I)$ non está cuberto por unha veciñanza coordenada. Sexa $\beta$ o supremo dos $b>t_0$ tales que existe un único transporte paralelo en $[t_0,b]$. Obviamente $\beta>t_0$, pois para $b$ suficientemente próximo a $t_0$, $[t_0,b]$ está contido nunha veciñanza coordenada. Por definición de supremo, existe un único transporte paralelo no intervalo $[t_0,\beta)$. Se $\beta$ é un punto interior de $I$, existe $\delta>0$ tal que $\alpha((\beta-\delta,\beta+\delta))$ está contido nunha veciñanza coordenada. Nesa veciñanza coordenada existe un único transporte paralelo $\tilde{V}$ tal que $\tilde{V}(\beta-\delta/2)=V(\beta-\delta/2)$ pola primeira parte da proba. Por unicidade, $V=\tilde{V}$ onde coincidan, e por tanto, iso significa que podemos estender $V$ ata $\beta+\delta$, o que contradí a definición de supremo. En consecuencia, $\beta$ non pode ser interior, e así $V$ está definido en tódolos puntos de $I$ á dereita de $t_0$. Un argumento similar para o lado esquerdo remataría a demostración.
Sexa $S$ unha superficie regular e $\alpha\colon I\to S$ unha curva regular.
Definímo-lo transporte paralelo ó longo de $\alpha$ dende $t_0$ ata $t_1$ como a aplicación linear \[ P(\alpha)_{t_0}^{t_1}\colon T_{\alpha(t_0)}S\to T_{\alpha(t_1)}S \] tal que $P(\alpha)_{t_0}^{t_1}(v)=V(t_1)$, sendo $V$ o único campo de vectores paralelo ó longo de $\alpha$ tal que $V(t_0)=v$.
Se $S$ é un plano e $\alpha\colon I\to S$ é unha curva, entón $P(\alpha)_{t_0}^{t_1}(v)=v$.
A aplicación transporte paralelo é unha isometría linear entre espacios vectoriais métricos.
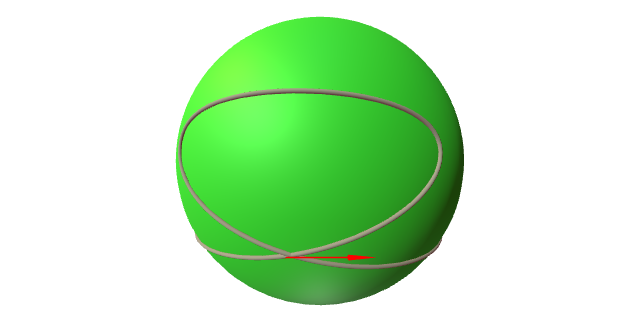
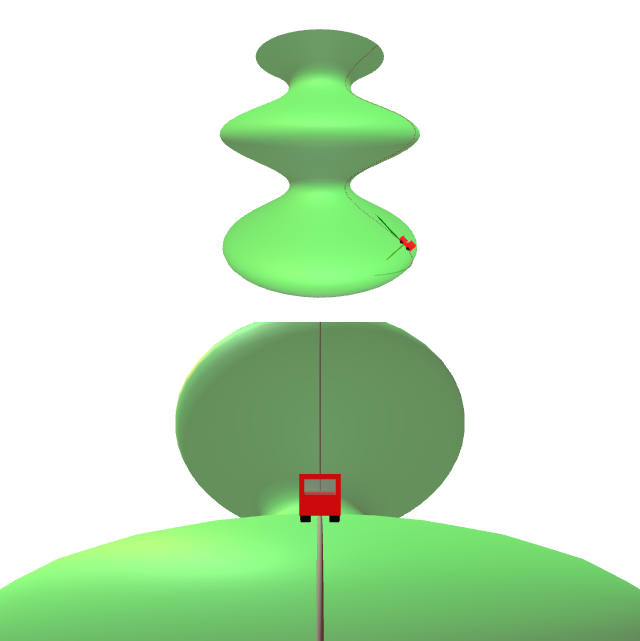
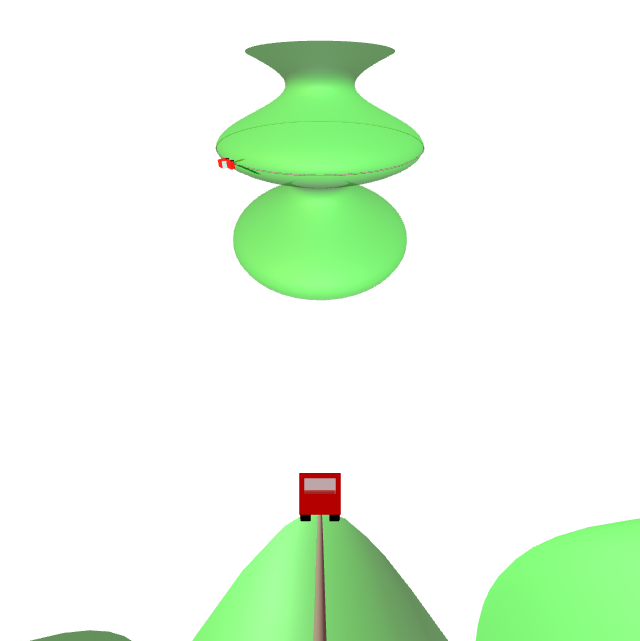
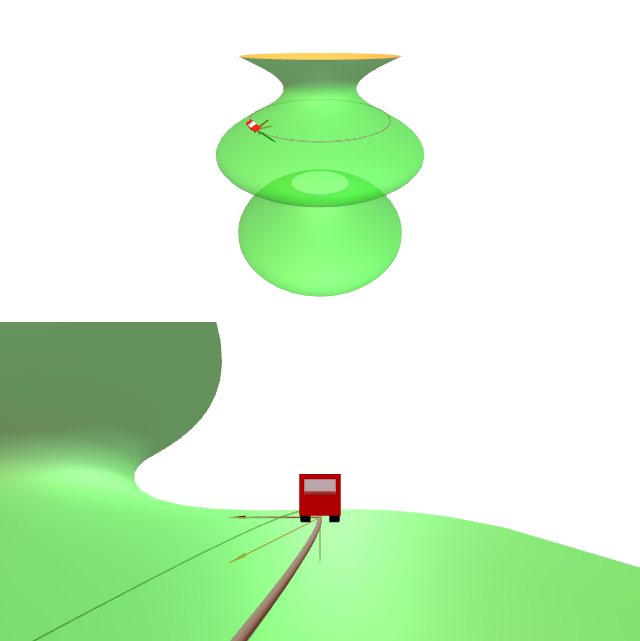
No gráfico amósase que para unha superficie non chá, transportar paralelamente ó longo dunha curva pechada non ten que ser necesariamente a identidade. Este é o fenómeno que se coñece como holonomía.