Orientación de superficies
Campos tanxentes e normais
Sexa $S$ unha superficie regular de $\R^3$.
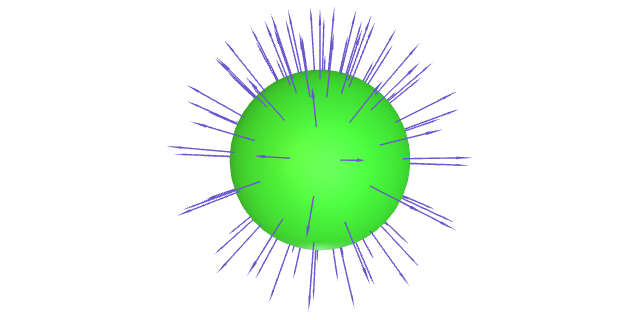
Un campo de vectores tanxente a $S$ é unha aplicación diferenciable $V\colon S\to \R^3$ tal que $V_p\in T_p S$ para todo $p\in S$.
Un campo de vectores normal a $S$ é unha aplicación diferenciable $V\colon S\to \R^3$ tal que $V_p$ é ortogonal a $T_p S$ para todo $p\in S$.
O seguinte gráfico presenta un campo de vectores tanxente e outro normal a unha superficie.

Sexa $\alpha\colon I\to S$ unha curva contida na superficie $S$. Un campo de vectores tanxente ó longo de $\alpha$ é unha aplicación diferenciable $V\colon I\to\R^3$ tal que $V(t)\in T_{\alpha(t)}S$ para todo $t\in I$.
Nótese que se a curva se autointerseca, un campo de vectores ó longo dunha curva pode ter múltiples definicións nun mesmo punto (dependendo de cantas veces a curva pase por ese punto).
Por outro lado, se $V$ é un campo de vectores tanxente a unha superficie $S$ e $\alpha\colon I \to S$ é unha curva, entón $W(t)=V_{\alpha(t)}$ define un campo de vectores ó longo de $\alpha$.
Coordenadas adaptadas
Sexa $V$ un campo de vectores tanxente a unha superficie regular $S$.
Unha curva integral de $V$ é unha curva $\alpha\colon I\to S$ tal que $\alpha'(t)=V_{\alpha(t)}$ para todo $t\in I$.
Sexa $\mathbf{x}\colon U\subset\R^2\to S$ unha parametrización de $S$. Podemos escribir en coordenadas $V_{\mathbf{x}(u_1,u_2)}=\sum_i V^i(u_1,u_2)\mathbf{x}_i(u_1,u_2)$ e $\alpha(t)=\mathbf{x}(u(t))$, $u(t)=(u_1(t),u_2(t))$. Entón, nesta veciñanza coordenada, $\alpha$ é curva integral de $V$ se e só se \[ u_i'(t)=V^i(u_1(t),u_2(t)),\quad i=1,2. \] Polo teorema de existencia e unicidade de ecuacións diferenciais ordinarias dedúcese que para cada $p\in S$ existe unha curva integral maximal $\alpha$ de $S$ tal que $\alpha(0)=p$.
Ademais, a dependencia diferenciable da solución xeral dunha EDO con respecto das condicións iniciais implica a existencia dunha aplicación $\phi\colon\mathcal{W}\to S$, con $\{0\}\times S\subset\mathcal{W}\subset\R\times S$, $\mathcal{W}$ aberto en $\R\times S$, tal que \[ \begin{aligned} \frac{\partial\phi}{\partial t}(t,p) &{}=V_{\phi(t,p)},\\ \phi(0,p) &{}=p. \end{aligned} \] Esta aplicación chámase o fluxo de $V$ e é habitual escribir $\phi_t(p)=\phi(t,p)$.
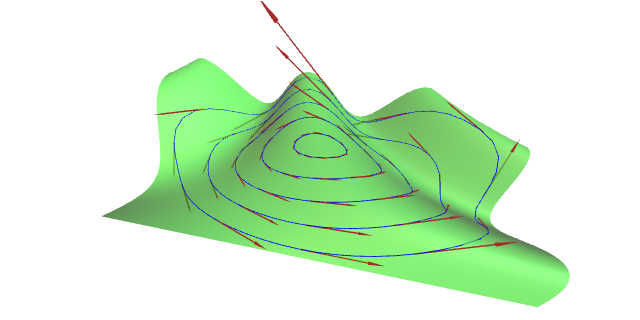
Probar $\phi_0=\id_S$, $\phi_t\circ\phi_s=\phi_{t+s}$, $\phi_t^{-1}=\phi_{-t}$.
Sexa $V$ un campo de vectores tanxente a unha superficie regular $S$, e $p\in S$ tal que $V_p\neq \mathbf{0}$. Entón existe unha parametrización $\mathbf{x}\colon U\subset\R^2\to S$ tal que $U=(-\epsilon,\epsilon)\times(-\epsilon,\epsilon)$, $\mathbf{x}(\mathbf{0})=p$, e $\mathbf{x}_1(q)=V_{\mathbf{x}(q)}$ para todo $q\in U$.
Nas condicións do lema do fluxo tubular é evidente que as curvas $t\mapsto\mathbf{x}(t,s_0)$ son curvas integrais de $V=\mathbf{x}_1$. Sexa $f$ a segunda coordenada de $\mathbf{x}^{-1}$. Entón,
- $f$ é constante ó longo das curvas integrais de $V$, pois $f(\mathbf{x}(t,s_0))=s_0$.
- $df_q\neq 0$ para todo $q\in\mathbf{x}(U)$, pois \[ \begin{aligned} df_{\mathbf{x}(t,s_0)}(\mathbf{x}_2) &{}=\frac{d}{ds}\bigg\vert_{0}f(\mathbf{x}(t,s_0+s))\\ &{}=\frac{d}{ds}\bigg\vert_0(s+s_0)=1. \end{aligned} \]
A unha función que satisfai estas dúas condicións chámaselle unha integral primeira de $V$. As integrais primeiras existen (localmente) polo que acabamos de ver.
Sexan $V_1$ e $V_2$ dous campos de vectores que son linearmente independentes nunha superficie regular $S$. Entón, dado $p\in S$ existe unha parametrización $\mathbf{x}\colon U\subset\R^2\to S$ tal que $\mathbf{x}(0,0)=p$ e $\mathbf{x}_i=a_i V_i$, $i=1,2$, con $a_1,a_2\colon\mathbf{x}(U)\to \R$ funcións diferenciables non nulas.
Arredor de cada punto existen coordenadas ortogonais.
Sexa $p\in S$ un punto non umbílico dunha superficie regular $S$. Entón, arredor de $p$ existe unha parametrización ortogonal de xeito que os campos coordenados son vectores principais.
Se $p$ é un punto non umbílico, por continuidade existe unha veciñanza de $p$ onde tódolos puntos son non umbílicos. Nesa veciñanza os campos de vectores principais unitarios están ben definidos, son diferenciables, e ortogonais polo teorema espectral. Para concluír basta con aplica-la proposición.
Unhas coordenadas como as que dá este último resultado denomínanse doblemente ortogonais.
As curvaturas principais e as direccións principais poden perde-la diferenciabilidade nos puntos umbílicos. Nese caso non se podería aplica-lo resultado anterior.
Orientación en espacios vectoriais
Sexa $V$ un espacio vectorial real de dimensión $n\geq 1$.
Dúas bases ordeadas de $V$, $(u_1,\dots,u_n)$ e $(v_1,\dots,v_n)$, dise que definen ou teñen a mesma orientación se a matriz de cambio de base dunha a outra ten determinante positivo. En caso contrario dise que teñen orientacións opostas.
A relación te-la mesma orientación
é unha relación de equivalencia no conxunto das bases de $V$.
O conxunto cociente desta relación ten exactamente dous elementos.
A elección dunha destas dúas clases de equivalencia dise que é unha orientación en $V$.
Unha base pertencente á clase de equivalencia escollida dise que está
positivamente orientada.
Un espacio vectorial real dise orientado se nel se escolleu unha orientación.
Podemos interpreta-la orientación dun espacio vectorial do seguinte xeito:
- Orientar un espacio vectorial de dimensión 1 é escoller "cara que lado van os números positivos".
- Orientar un espacio vectorial de dimensión 2 é escoller un "sentido de xiro".
- Supoñamos que en $\R^3$ témo-la orientación canónica. Entón, orientar un plano $P$ en $\R^3$ é equivalente á elección dun vector normal unitario a $P$: se $(\mathbf{u}_1,\mathbf{u}_2)$ é unha base positivamente orientada de $P$, escollémo-lo vector normal unitario $\frac{\mathbf{u}_1\times \mathbf{u}_2}{\lVert \mathbf{u}_1\times \mathbf{u}_2\rVert}$. Recordemos que se $(\mathbf{v}_1,\mathbf{v}_2)$ é outra base de $P$ e $\mathbf{v}_i=A(\mathbf{u}_i)$, entón \[ \frac{\mathbf{v}_1\times \mathbf{v}_2}{\lVert \mathbf{v}_1\times \mathbf{v}_2\rVert} =\mathop{\rm signo}(\det A) \frac{\mathbf{u}_1\times \mathbf{u}_2}{\lVert \mathbf{u}_1\times \mathbf{u}_2\rVert}. \]
Sexan $V$ e $W$ dous espacios vectorias e $F\colon V\to W$ un isomorfismo linear. Dicimos que $F$ preserva a orientación se leva bases positivamente orientadas de $V$ en bases positivamente orientadas de $W$. En caso contrario, dicimos que $F$ invirte a orientación.
Orientación en superficies
Sexa $S$ unha superficie. Sexan $\mathbf{x}\colon U\subset\R^2\to S$ e $\mathbf{y}\colon V\subset\R^2\to S$ dúas parametrización de $S$ tales que $\mathbf{x}(U)\cap\mathbf{y}(V)\neq\emptyset$.
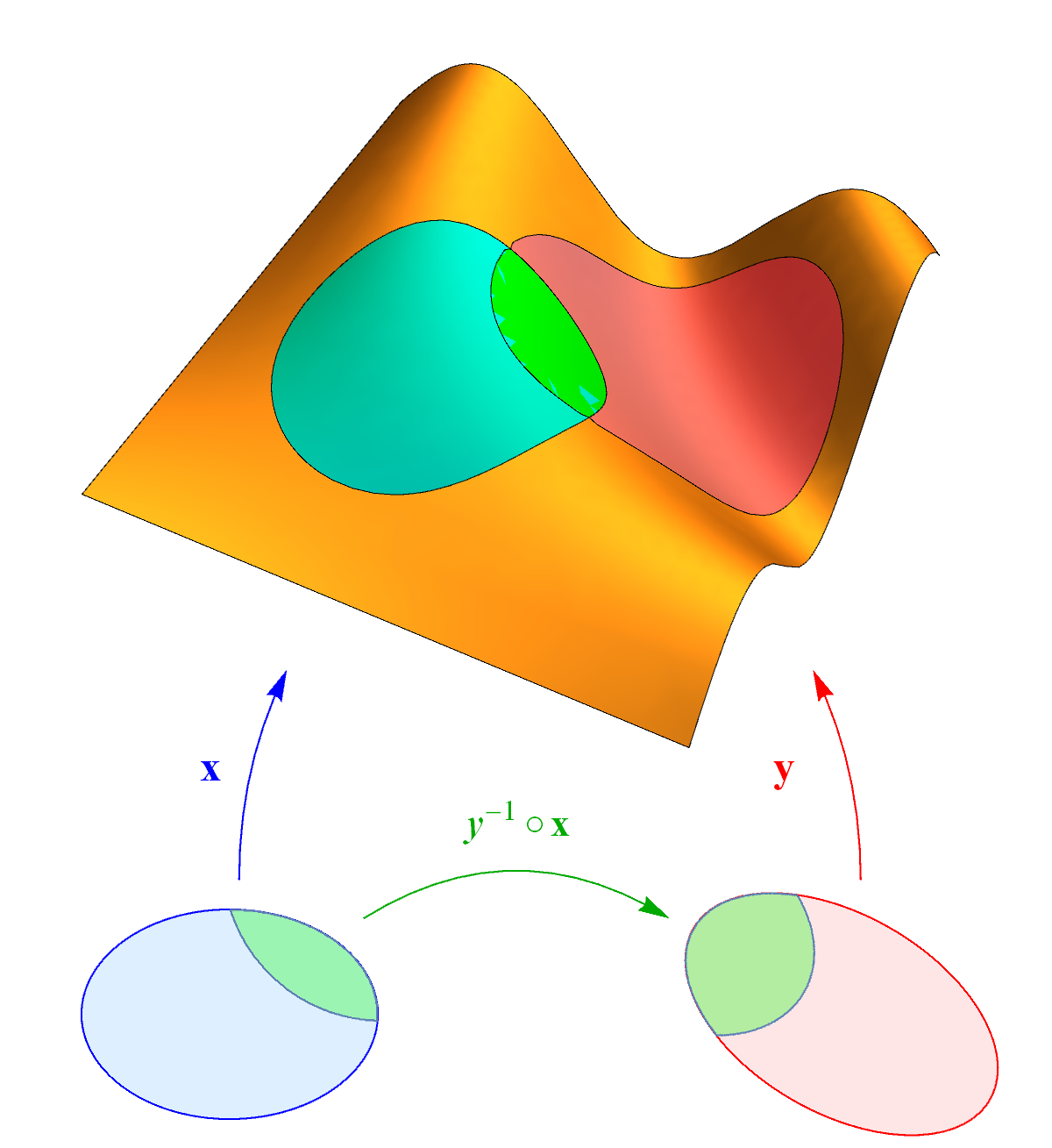
Sabemos que a aplicación de cambio de coordenadas \[ \mathbf{y}^{-1}\circ\mathbf{x}\colon\mathbf{x}^{-1}(\mathbf{x}(U)\cap\mathbf{y}(V))\to\mathbf{y}^{-1}(\mathbf{x}(U)\cap\mathbf{y}(V)) \] é unha aplicación diferenciable. A continuación recordamos como se relacionan os campos de vectores coordenados $\{\mathbf{x}_1,\mathbf{x}_2\}$ e $\{\mathbf{y}_1,\mathbf{y}_2\}$ nun punto da intersección.
Poñamos \[ (\mathbf{y}^{-1}\circ\mathbf{x})(u_1,u_2)=(v_1(u_1,u_2),v_2(u_1,u_2)). \] Temos \[ \mathbf{x}_i(u_1,u_2) =\sum_j \frac{\partial v_j}{\partial u_i}(u_1,u_2)\, \mathbf{y}_j(v_1(u_1,u_2),v_2(u_1,u_2)), \] ou ben, matricialmente, \[ \begin{pmatrix} \mathbf{x}_1 & \mathbf{x}_2 \end{pmatrix} = \begin{pmatrix} \mathbf{y}_1 & \mathbf{y}_2 \end{pmatrix} \begin{pmatrix} \frac{\partial v_1}{\partial u_1} & \frac{\partial v_1}{\partial u_2}\\ \frac{\partial v_2}{\partial u_1} & \frac{\partial v_2}{\partial u_2} \end{pmatrix}, \] é dicir, que a matriz de cambio de base de $\{\mathbf{x}_1,\mathbf{x}_2\}$ a $\{\mathbf{y}_1,\mathbf{y}_2\}$ é $d(\mathbf{y}^{-1}\circ\mathbf{x})=\Bigl(\frac{\partial v_j}{\partial u_i}\Bigr)$. Obviamente esta matriz é non singular e por tanto o seu determinante é non nulo.
Nótese que ademais, \[ \frac{\mathbf{x}_1\times\mathbf{x}_2}{\lVert\mathbf{x}_1\times\mathbf{x}_2\rVert} =(\mathop{\rm signo}\det d(\mathbf{y}^{-1}\circ\mathbf{x})) \frac{\mathbf{y}_1\times\mathbf{y}_2}{\lVert\mathbf{y}_1\times\mathbf{y}_2\rVert}. \]
Unha superficie $S$ dise orientable se existe unha familia de parametrizacións $\{\mathbf{x}^\lambda\colon U_\lambda\to S\}_{\lambda\in\Lambda}$ tales que $S=\cup_{\lambda\in\Lambda}\mathbf{x}(U_\lambda)$ e cando queira que $\mathbf{x}^\lambda(U_\lambda)\cap\mathbf{x}^\mu(U_\mu)\neq\emptyset$ temos $\det d((\mathbf{x}^\mu)^{-1}\circ\mathbf{x}^\lambda) > 0$.
A superficie dise orientada cando facemos unha escolla de parametrizacións nas condicións anteriores.
Sexa $S$ unha superficie orientada. Unha parametrización $\mathbf{x}$ dise positivamente orientada se $\det d(\mathbf{x}^{-1}\circ\mathbf{x}^\lambda) > 0$ para algunha parametrización $\mathbf{x}^\lambda$ que determina a orientación de $S$. En caso contrario dise negativamente orientada.
En particular, se $S$ está orientada, para cada $p\in S$ o espacio tanxente $T_p S$ está orientado pola base de campos de vectores coordenados dunha parametrización positivamente orientada. É dicir, se $\mathbf{x}\colon U\subset\R^2\to S$ é unha parametrización positivamente orientada con $p=\mathbf{x}(q)$, entón a orientación de $T_p S$ está na clase de equivalencia da base $(\mathbf{x}_1(q),\mathbf{x}_2(q))$.
Sexan $S_1$ e $S_2$ dúas superficies orientadas. Un difeomorfismo $f\colon S_1\to S_2$ dise que preserva a orientación se para para todo $p\in S_1$, $df_p\colon T_p S_1\to T_{f(p)}S_2$ preserva a orientación no sentido de espacios vectoriais orientados.
Na situación anterior, se $df_p\colon T_p S_1\to T_{f(p)}S_2$ invirte a orientación para todo $p\in S_1$, dise que $f$ invirte a orientación.
Ademais, nas condicións da definición, se $S_1$ é conexa (e por tanto $S_2$ tamén), un difeomorfismo preserva ou invirte a orientación.
Probar que un difeomorfismo entre superficies orientadas $f\colon S_1\to S_2$ preserva a orientación se e só se para cada parametrización positivamente orientada $\mathbf{x}\colon U\subset\R^2\to S_1$ de $S_1$, $f\circ\mathbf{x}$ é unha parametrización positivamente orientada de $S_2$.
Sexa $f\colon S_1\to S_2$ un difeomorfismo entre superficies orientadas, con $S_1$ conexa. Probar que $f$ preserva a orientación se e só se existe $p\in S_1$ tal que a diferencial $df_p\colon T_p S_1\to T_{f(p)}S_2$ preserva a orientación.
Unha superficie $S$ de $\R^3$ é orientable se e só se existe un campo de vectores diferenciable, normal, e unitario $\mathbf{N}$ definido en toda a superficie $S$.
Probar que se $S$ é unha superficie regular, conexa e orientable, entón existen exactamente dous campos de vectores diferenciables, normais e unitarios definidos en $S$.
Sexa $f\colon U\subset\R^3\to\R$ unha función diferenciable e $a\in f(U)$ un valor regular de $f$. Entón $S=f^{-1}(a)$ é unha superficie regular orientable.
Se $S$ é unha superficie orientada e $\mathbf{N}$ é un campo de vectores diferenciable, normal, e unitario, dise que $\mathbf{N}$ está positivamente orientado se para calquera parametrización positivamente orientada $\mathbf{x}$ se ten $\mathbf{N}=\frac{\mathbf{x}_1\times\mathbf{x}_2}{\lVert \mathbf{x}_1\times\mathbf{x}_2\rVert}$. Neste caso, $(\mathbf{x}_1,\mathbf{x}_2,\mathbf{N})$ é unha base positivamente orientada de $\R^3$.
Sexa $S$ unha superficie orientada cun campo de vectores normal e unitario $\mathbf{N}$ positivamente orientado. Probar que unha base (ordeada) $(v_1,v_2)$ de $T_p S$ está positivamente orientada se e só se $\det(v_1,v_2,\mathbf{N}_p) > 0$.
O exemplo prototípico de superficie non orientable é a banda de Möbius. Esta superficie obtense "topoloxicamente" pegando en sentido contrario os extremos opostos dos laterais dun rectángulo. A continuación explicamos un posible xeito de realizar analiticamente esta construcción.
A banda de Möbius pode obterse rotando un segmento ó longo dunha circuferencia coa metade de ángulo có punto desa circunferencia. O gráfico seguinte exemplifica dita construcción.
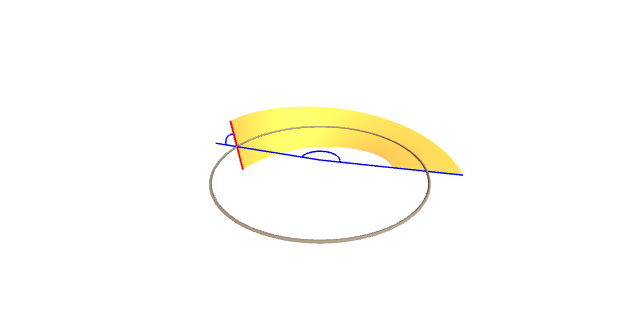
Consideremos unha circunferencia de radio $r$ no plano $z=0$. Dita circunferencia pode parametrizarse mediante a curva $\theta\mapsto r(\cos\theta, \sin\theta,0)$, con $\theta\in[0,2\pi]$. Tomamos un segmento horizontal no punto $\theta=0$, digamos por exemplo $\{(r+t,0,0):t\in(-l,l)\}$.
A continuación facemos un movemento de traslación ó longo da circunferencia ó mesmo tempo que facemos unha rotación do segmento de xeito que cando o segmento leve percorrido un ángulo $\theta$, o ángulo de rotación do segmento sexa de $\theta/2$. Por tanto, o primeiro paso é rota-lo segmento un ángulo $\theta/2$ arredor do punto $(r,0,0)$ no plano $y=0$; para iso primeiro trasladamos á orixe, rotamos arredor da orixe no plano $y=0$ e despois volvemos trasladar a $(r,0,0)$: \[ \begin{pmatrix} \cos\frac{\theta}{2} & 0 & -\sin\frac{\theta}{2}\\ 0 & 1 & 0\\ \sin\frac{\theta}{2} & 0 & \cos\frac{\theta}{2} \end{pmatrix} \left( \begin{pmatrix} r+t\\ 0\\ 0 \end{pmatrix} - \begin{pmatrix} r\\ 0\\ 0 \end{pmatrix} \right) + \begin{pmatrix} r\\ 0\\ 0 \end{pmatrix} = \begin{pmatrix} r+t\cos\frac{\theta}{2}\\ 0\\ t\sin\frac{\theta}{2} \end{pmatrix}. \]
Agora rotámo-lo segmento así obtido arredor da orixe con respecto ó eixo $z$ un ángulo $\theta$: \[ \begin{pmatrix} \cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} r+t\cos\frac{\theta}{2}\\ 0\\ t\sin\frac{\theta}{2} \end{pmatrix} = \begin{pmatrix} \bigl(r+t\cos\frac{\theta}{2}\bigr)\cos\theta\\ \bigl(r+t\cos\frac{\theta}{2}\bigr)\sin\theta\\ t\sin\frac{\theta}{2} \end{pmatrix} \]
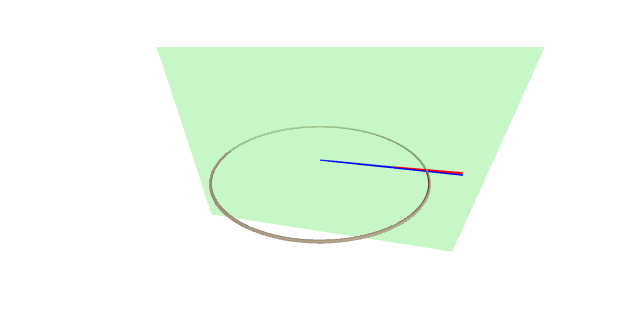
A traxectoria deste segmento determina a banda de Möbius, que por tanto é a imaxe da aplicación $F\colon\R\times(-l,l)\to\R^3$ definida como \[ F(\theta,t)= \Bigl(\Bigl(r+t\cos\frac{\theta}{2}\Bigr)\cos\theta,\, \Bigl(r+t\cos\frac{\theta}{2}\Bigr)\sin\theta,\, t\sin\frac{\theta}{2}\Bigr). \]
Podemos recubri-la banda de Möbius mediante dúas parametrizacións: $\mathbf{x}=F_{\vert(0,2\pi)\times(-l,l)}$ e $\mathbf{y}=F_{\vert(-\pi,\pi)\times(-l,l)}$.
No gráfico seguinte preséntase visualmente a demostración de que a banda de Möbius non é orientable, xa que non é posible definir un campo normal unitario continuo ó longo da mesma.
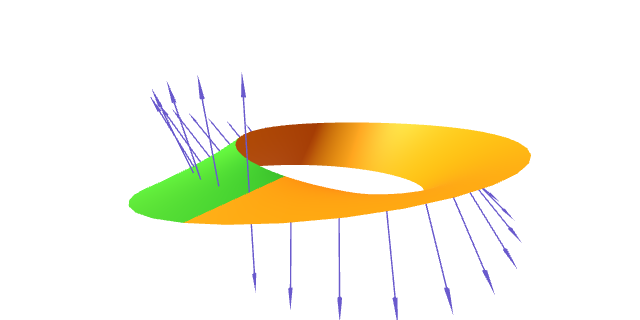
A banda de Möbius non é orientable.
Supoñamos pola contra que si é orientable, é dicir, que existe un campo de vectores normal unitario $\mathbf{N}$ definido en toda a superficie. Podemos supoñer, cambiando o signo de $\mathbf{N}$ se fose necesario, que \[ \mathbf{N}= \frac{\mathbf{x}_\theta\times\mathbf{x}_t} {\lVert\mathbf{x}_\theta\times\mathbf{x}_t\rVert} \] en $\mathbf{x}\bigl((0,2\pi)\times(-l,l)\bigr)$, xa que esta veciñanza coordenada é conexa.
Derivando temos \[ \begin{aligned} \mathbf{x}_\theta(\theta,0) & {}=(-r\sin\theta,r\cos\theta,0),\\[1ex] \mathbf{x}_t(\theta,0) & {}=\Bigl(-\sin\frac{\theta}{2}\cos\theta,\, -\sin\frac{\theta}{2}\sin\theta,\, \cos\frac{\theta}{2}\Bigr). \end{aligned} \] Calculando o producto vectorial e dividindo pola normal teriamos \[ \mathbf{N}_{\mathbf{x}(\theta,0)} =\Bigl(\cos\frac{\theta}{2}\cos\theta, \cos\frac{\theta}{2}\sin\theta, \sin\frac{\theta}{2}\Bigr). \]
Agora mirámo-lo que pasa no punto $p=F(0,0)=(r,0,0)$. Por continuidade, debemos ter \[ \begin{aligned} \mathbf{N}_p &{}=\lim_{\theta\to 0^+}\mathbf{N}_{\mathbf{x}(\theta,0)}\\ &{}=\lim_{\theta\to 0^+}\, \Bigl(\cos\frac{\theta}{2}\cos\theta, \cos\frac{\theta}{2}\sin\theta, \sin\frac{\theta}{2}\Bigr)\\[1ex] &{}=(1,0,0). \end{aligned} \] Pero tamén \[ \begin{aligned} \mathbf{N}_p &{}=\lim_{\theta\to 2\pi^-}\mathbf{N}_{\mathbf{x}(\theta,0)}\\ &{}=\lim_{\theta\to 2\pi^-}\, \Bigl(\cos\frac{\theta}{2}\cos\theta, \cos\frac{\theta}{2}\sin\theta, \sin\frac{\theta}{2}\Bigr)\\[1ex] &{}=(-1,0,0), \end{aligned} \] o que nos dá unha contradicción. Por tanto, a banda de Möbius non é orientable.
Os seguintes resultados van máis aló dos obxectivos deste curso:
- Toda superficie pechada orientable de $\R^3$ é imaxe recíproca dun valor regular dalgunha función.
- Toda superficie compacta de $\R^3$ é orientable (Teorema de Brouwer-Samelson). Por tanto, $\R\mathsf{P}^2$ é unha superficie (abstracta) compacta que non se pode ver como superficie regular de $\R^3$ porque non é orientable.
Estructura complexa dunha superficie orientada
Sexa $S$ unha superficie orientada cun campo de vectores normal e unitario $\mathbf{N}$ positivamente orientado.
Defínese a estructura complexa de $S$ en $p\in S$ como a aplicación linear $J_p\colon T_p S\to T_p S$ dada por \[ J_p(v)=\mathbf{N}_p\times v. \]
Se $v\in T_p S$ é non nulo entón $(v,J_p(v))$ é unha base positivamente orientada.
Se $\alpha\colon I\to S$ é unha curva regular contida en $S$, entón defínese $J\alpha'$ como o campo de vectores tanxente ó longo de $\alpha$ que vén dado por $J\alpha'(t)=J_{\alpha(t)}(\alpha'(t))$ para cada $t\in I$.
Se $S$ é unha superficie orientada, e $\alpha\colon I\to S$ é unha curva en $S$, entón $(\alpha'(t),J\alpha'(t))$ é unha base positivamente orientada de $T_{\alpha(t)}S$ para cada $t\in I$.