Teorema de Gauss-Bonnet
O obxectivo deste tema é proba-la fórmula de Gauss-Bonnet, que relaciona un concepto local puramente xeométrico como é a curvatura de Gauss, con outro global de corte topolóxico chamado a característica de Euler.
\[ \int_R K+\int_{\partial R}\kappa_g+\sum_{i=1}^k\epsilon_i=2\pi\chi(R). \]
\[ \int_S K = 2\pi\chi(S). \]
Ángulo de rotación dunha curva
Empezamos con algúns resultados para curvas planas.
Sexa $\alpha\colon[a,b]\to\R^2$ unha curva plana parametrizada por arco. Sexa $\{e_1,e_2\}$ unha base ortonormal de $\R^2$ e $s_0\in[a,b]$. Entón existe unha función $\theta\colon[a,b]\to\R$ tal que \[ \alpha'(s)=\bigl(\cos\theta(s)\bigr)e_1+\bigl(\sin\theta(s)\bigr)e_2, \] e $\theta(s_0)$ é o ángulo que forman $\alpha'(s_0)$ e $e_1$.
Podemos escribir $\alpha'(s)=a(s)e_1+b(s)e_2$. Como $a=\langle\alpha',e_1\rangle$ e $b=\langle\alpha',e_2\rangle$, estas funcións son diferenciables. Denotemos por $\theta_0$ o ángulo que forman $\alpha'(s_0)$ e $e_1$. Definimos \[ \theta(s)= \theta_0 +\int_{s_0}^s\bigl(a(t)b'(t)-b(t)a'(t)\bigr)\textup{d}t. \]
Claramente $\theta(s_0)=\theta_0$. Para remata-la demostración chega con ver que a función \[ f(s)=\bigl(a(s)-\cos\theta(s)\bigr)^2+\bigl(b(s)-\sin\theta(s)\bigr)^2 \] é identicamente nula.
Por definición de $\theta_0$ temos \[ f(s_0)=\bigl(a(s_0)-\cos\theta_0\bigr)^2+\bigl(b(s_0)-\sin\theta_0\bigr)^2=0. \] Por outra banda, \[ \begin{aligned} f' &{}=-a(a^2+b^2)'\cos\theta-b(a^2+b^2)'\sin\theta=0, \end{aligned} \] de onde se deduce que $f=0$ como queriamos probar.
O ángulo de rotación total dunha curva plana parametrizada por arco $\alpha\colon[a,b]\to\R^2$ defínese como $\theta(b)-\theta(a)$, sendo $\theta$ un ángulo de rotación.
Nótese que se $\tilde{\theta}$ é outra función tal que \[ \alpha'(s)=\bigl(\cos\tilde{\theta}(s)\bigr)e_1 +\bigl(\sin\tilde{\theta}(s)\bigr)e_2, \] teriamos $\theta(s)=\tilde{\theta}(s)+2k(s)\pi$, sendo $k(s)\in\mathbb{Z}$. Por continuidade $k(s)$ é constante, e así o ángulo de rotación está ben definido.
Se $\alpha$ é pechada, é dicir, $\alpha(a)=\alpha(b)$ e $\alpha'(a)=\alpha'(b)$, entón o ángulo de rotación $\theta(b)-\theta(a)$ é un múltiplo enteiro de $2\pi$, xa que nese caso $\cos\theta(a)=\cos\theta(b)$, $\sin\theta(a)=\sin\theta(b)$.
Nas seguintes figuras preséntanse varios ángulos de rotación total.
Recordemos que unha curva admisible é unha aplicación continua $\alpha\colon[a,b]\to S$ tal que existe unha parametrización $a=t_0<a_1<\dots<t_k=b$ de xeito que $\alpha{\vert [t_i,t_{i+1}]}$ é unha curva regular para cada $i=1,\dots,k$. Os puntos $\alpha(t_i)$ son os vértices da curva. Recordemos \[ \begin{aligned} \alpha'(t_i^-) &{}=\lim_{t\to t_i^-}\alpha'(t_i),\\ \alpha'(t_i^+) &{}=\lim_{t\to t_i^+}\alpha'(t_i). \end{aligned} \] Tal curva pode ser parametrizada por parámetro lonxitude de arco.
Dise que $\alpha$ é pechada se $\alpha(a)=\alpha(b)$. A curva dise simple se $\alpha$ é unha función inxectiva.
Supoñamos agora que $\alpha\colon[a,b]\to\R^2$ é unha curva plana admisible, pechada, simple, e parametrizada por arco a trozos. Polo teorema da curva de Jordan, $\alpha([a,b])$ divide o plano en exactamente dúas rexións, unhas das cales, chamémoslle $R$, é relativamente compacta e simplemente conexa. Esta rexión $R$ chámase a rexión interior.
Supoñamos que o plano $\R^2$ está orientado de acordo a unha base. Dicimos que $\alpha$ está positivamente orientada se $J\alpha'(s)$ apunta ó interior de $\alpha$ (é dicir, se $\beta\colon [0,\epsilon)\to \overline{R}$ é tal que $\beta(0)=\alpha(s)$ e $\beta'(0)\neq\alpha'(s)$, entón $\langle\beta'(0),J\alpha'(0)\rangle > 0$).
Sexa $\alpha\colon[a,b]\to\R^2$ unha curva plana parametrizada por arco a trozos (curva admisible) con respecto da partición $a=s_0<s_1<\dots<s_k=b$. Defínese o ángulo exterior no vértice $\alpha(s_i)$ como o número $\epsilon_i\in[-\pi,\pi]$ tal que \[ \alpha'(s_i^+)=\bigl(\cos\epsilon_i\bigr)\alpha'(s_i^-) +\bigl(\sin\epsilon_i\bigr)J\alpha'(s_i^-), \] sendo $J$ a estructura complexa de $\R^2$ (con respecto da orientación elexida).
No que segue suporemos que cada vértice $\alpha(s_i)$ é un vértice de verdade, é dicir, que $\alpha'(s_i^-)\neq\alpha'(s_i^+)$, co que $\epsilon_i\neq 0$.
Nótese tamén que farémo-lo pequeno abuso de notación (xa que a curva é pechada, $\alpha(a)=\alpha(b)$), de que $\alpha'(s_k^+)=\alpha'(b^+)\equiv\alpha'(a^+)=\alpha'(s_0^+)$.
O ángulo $\epsilon_i$ pode ser positivo ou negativo dependendo da orientación e do sentido de xiro.
Se $\alpha'(s_i^-)$ e $\alpha'(s_i^+)$ son opostos, dicimos que o vértice forma unha cúspide. Neste caso hai que decidir se o ángulo é $\pi$ ou $-\pi$. Neste curso non trataremos este caso, aínda que pode definirse por continuidade.
Neste curso omitirémo-la demostración do resultado coñecido como Hopf Umlaufsatz para curvas regulares a trozos.
Se $\alpha$ é unha curva regular a trozos en $s_0< s_1<\dots < s_k$ pechada, simple e orientada positivamente, $\theta_i\colon[s_{i-1},s_i]\to\R$ denota o ángulo de rotación en cada parte regular, e $\epsilon_i$ o ángulo exterior en cada vértice $\alpha(s_i)$, $i\in\{1,\dots,k\}$, entón \[ \sum_{i=1}^k\bigl(\theta_i(s_i)-\theta_i(s_{i-1})\bigr) +\sum_{i=1}^k\epsilon_i=2\pi. \]
Se a curva está negativamente orientada, simplemente cambia o signo no lado dereito da igualdade.
Comprobámo-lo teorema de rotación das tanxentes para a curva $\alpha\colon [0,3]\to \R^2$ dada por \[ \alpha(t)= \begin{cases} (t,t^2) & t\in [0,1],\\ (2-t,1) & t\in[1,2],\\ (0,3-t) & t\in[2,3]. \end{cases} \]
O seguinte debuxo dá unha demostración gráfica do teorema de rotación dos tanxentes.
Outro exemplo visual do ángulo de rotación.
Supoñamos agora que $S$ é unha superficie orientada con estructura complexa $J$. Sexa $\alpha\colon[a,b]\to S$ unha curva admisible pechada e simple na partición $a=s_0<s_1<\dots<s_k=b$. Supoñamos que $\mathbf{x}\colon U\to S$ é unha parametrización positiva, $U$ é homeomorfo a unha bóla de $\R^2$, e $\alpha([a,b])\subset U$. O ángulo de rotación mídese con respecto a $\mathbf{x}_1$ e todo o demais pode repetirse para este caso.
Coordenadas ortogonais
Os seguinte preparativo que necesitamos para a demostración do teorema de Gauss-Bonnet é obter algúns resultados para parametrizacións ortogonais. Nótese que estas existen: por exemplo, as coordenadas polares xeodésicas. De xeito máis específico, existen coordenadas ortogonais arredor de cada punto da superficie.
Sexan $\mathbf{x}\colon U\to S$ coordenadas ortogonais, é dicir, $g_{12}=0$. Entón, témo-los símbolos de Christoffel:
Os símbolos de Christoffel nunha parametrización ortogonal son: \[ \begin{aligned} \Gamma_{11}^1 &{}=\frac{1}{2g_{11}}\frac{\partial g_{11}}{\partial u_1},\\ \Gamma_{11}^2 &{}=-\frac{1}{2g_{22}}\frac{\partial g_{11}}{\partial u_2},\\ \Gamma_{12}^1 &{}=\Gamma_{21}^1 =\frac{1}{2g_{11}}\frac{\partial g_{11}}{\partial u_2},\\ \Gamma_{12}^2 &{}=\Gamma_{21}^2 =\frac{1}{2g_{22}}\frac{\partial g_{22}}{\partial u_1},\\ \Gamma_{22}^1 &{}=-\frac{1}{2g_{11}}\frac{\partial g_{22}}{\partial u_1},\\ \Gamma_{22}^2 &{}=\frac{1}{2g_{22}}\frac{\partial g_{22}}{\partial u_2}. \end{aligned} \]
A partir de agora supoñemos que $S$ é unha superficie orientada, e que $\mathbf{x}\colon U\subset\R^2\to S$ é unha parametrización ortogonal orientada positivamente.
Sexa $S$ unha superficie orientada. Sexa $\mathbf{x}\colon U\subset\R^2\to S$ unha parametrización ortogonal de $S$ positivamente orientada. Sexa $\alpha\colon I\to\mathbf{x}(U)$ unha curva regular parametrizada por arco con ángulo de rotación $\theta$. Poñamos $\alpha(s)=\mathbf{x}(u_1(s),u_2(s))$. Entón \[ \kappa_g[\alpha]=\theta'+\frac{1}{2\sqrt{g_{11}g_{22}}}\Bigl( -u_1'\frac{\partial g_{11}}{\partial u_2} +u_2'\frac{\partial g_{22}}{\partial u_1} \Bigr). \]
Definimos \[ \begin{aligned} E_1(s) &{}=\frac{\mathbf{x}_1(u(s))}{\lVert\mathbf{x}_1(u(s))\rVert},\\ E_2(s) &{}=\frac{\mathbf{x}_2(u(s))}{\lVert\mathbf{x}_2(u(s))\rVert}. \end{aligned} \] Entón $(E_1,E_2)$ é unha base ortonormal positivamente orientada ó longo de $\alpha$. En particular, $JE_1=E_2$, $JE_2=-E_1$.
O ángulo de rotación $\theta$ vén definido pola ecuación \[ \alpha'(s)= \bigl(\cos\theta(s)\bigr)E_1(s) +\bigl(\sin\theta(s)\bigr)E_2(s). \]
Por un lado temos \[ J\alpha'=-(\sin\theta)E_1+(\cos\theta)E_2. \] Por outro lado, \[ \frac{D\alpha'}{ds} =\bigl(\theta'+\langle E_1',E_2\rangle\bigr) \bigl(-(\sin\theta)E_1+(\cos\theta)E_2\bigr). \] En consecuencia, \[ \begin{aligned} \kappa_g[\alpha] &{}=\Bigl\langle \frac{D\alpha'}{ds},J\alpha'\Bigr\rangle\\ &{}=\theta'+\langle E_1',E_2\rangle. \end{aligned} \]
Finalmente, tendo en conta a expresión para os símbolos de Christoffel nunha parametrización ortogonal, obtemos \[ \langle E_1',E_2\rangle =\frac{1}{2\sqrt{g_{11}g_{22}}}\Bigl( -u_1'\frac{\partial g_{11}}{\partial u_2} +u_2'\frac{\partial g_{22}}{\partial u_1} \Bigr), \] de onde se deduce o resultado.
Tamén necesitarémo-la seguinte fórmula, que se proba simplemente empregando a ecuación de Gauss e os símbolos de Christoffel calculadas anteriormente.
Sexa $\mathbf{x}\colon U\subset\R^2\to S$ unha parametrización ortogonal de $S$ positivamente orientada. Entón \[ K=-\frac{1}{2\sqrt{g_{11}g_{22}}}\biggl( \frac{\partial}{\partial u_1}\Bigl( \frac{1}{\sqrt{g_{11}g_{22}}}\frac{\partial g_{22}}{\partial u_1} \Bigr) +\frac{\partial}{\partial u_2}\Bigl( \frac{1}{\sqrt{g_{11}g_{22}}}\frac{\partial g_{11}}{\partial u_2} \Bigr) \biggr). \]
Teorema de Gauss-Bonnet local
Recordemos que a integral de liña de $f\colon I\to \R$ ó longo da curva $\alpha\colon I\to \R^n$ se define como \[ \int_\alpha f=\int_I f(t)\lVert\alpha'(t)\rVert\,\textup{d}t. \]
A integral de superficie dunha función $f\colon U\to S$ ó longo (da parametrización $\mathbf{x}\colon U\subset\R^2\to S$) dunha superficie $S$ defínese como \[ \int_S f=\int_{U} f(u,v)\lVert\mathbf{x}_u(u,v)\times\mathbf{x}_v(u,v)\rVert\, \textup{d}u\,\textup{d}v. \]
Recordamos tamén un dos teoremas básicos do cálculo vectorial.
Sexa $R$ unha rexión de $\R^2$ e supoñamos que $\alpha \colon I\to\partial R$ parametriza (a trozos) a fronteira $\partial R$ con coordenadas $\alpha(t)=(x(t),y(t))$. Se $P,Q\colon R\to\R$ son funcións diferenciables, entón \[ \int_{\partial R} P\,\textup{d}x+Q\,\textup{d}y =\int_R \Bigl(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\Bigr) \,\textup{d}x\,\textup{d}y. \]
Escrito de xeito máis explícito: \[ \int_I \bigl(P(\alpha(t))x'(t)+Q(\alpha(t))y'(t)\bigr)\textup{d}t =\int_R \Bigl(\frac{\partial Q}{\partial x}(x,y) -\frac{\partial P}{\partial y}(x,y)\Bigr) \,\textup{d}x\,\textup{d}y. \]
Podemos agora proba-la primeira versión do teorema de Gauss-Bonnet.
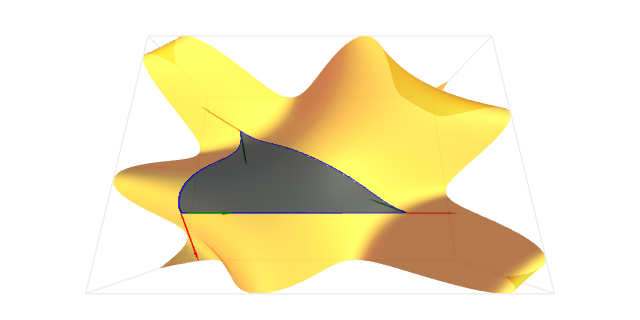
Sexa $S$ unha superficie regular e $\mathbf{x}\colon U\subset\R^2\to S$ unha parametrización ortogonal con $U$ homeomorfo a unha bóla. Sexa $R\subset\mathbf{x}(U)$ unha rexión simple e $\alpha\colon[a,b]\to \partial R$ unha parametrización do borde, positivamente orientada, por arco a trozos con respecto da partición $a=s_0< s_1<\dots < s_k=b$. Sexan $\epsilon_1,\dots,\epsilon_k$ os ángulos exteriores nos vértices $\alpha(s_1),\dots,\alpha(s_k)$. Entón, \[ \int_R K+\int_{\partial R}\kappa_g+\sum_{i=1}^k\epsilon_i=2\pi. \]
Escribamos $\alpha(s)=\mathbf{x}(u(s))$ con $u(s)=(u_1(s),u_2(s))$. Tamén tomámo-las funcións $P,Q\colon U\to\R$ definidas como \[ \begin{aligned} P &{}=-\frac{1}{2\sqrt{g_{11}g_{22}}}\frac{\partial g_{11}}{\partial u_2},\\ Q &{}=\frac{1}{2\sqrt{g_{11}g_{22}}}\frac{\partial g_{22}}{\partial u_1}. \end{aligned} \]
Empregando a fórmula para a curvatura xeodésica en coordenadas ortogonais, obtemos, nos puntos de regularidade de $\alpha$, \[ \kappa_g =\theta'+(P\circ u) u_1'+(Q\circ u) u_2'. \] Similarmente, comparando coa fórmula para a curvatura de Gauss en coordenadas ortogonais, \[ K\circ\mathbf{x}=\frac{1}{\sqrt{g_{11}g_{22}}}\left( \frac{\partial Q}{\partial u_1} -\frac{\partial P}{\partial u_2} \right) \]
Por tanto, utilizando o teorema de rotación das tanxentes e o teorema de Green obtemos \[ \begin{aligned} \int_{\partial R}\kappa_g &{}=\sum_{i=1}^k\int_{s_{i-1}}^{s_i} \kappa_g(s)\lVert\alpha'(s)\rVert\,\textup{d}s\\ &{}=\sum_{i=1}^k\bigl(\theta(s_i)-\theta(s_{i-1})\bigr) +\sum_{i=1}^k\int_{s_{i-1}}^{s_i} \Bigl(P(u(s))u_1'(s)+Q(u(s))u_2(s)\Bigr)\,\textup{d}s\\ &{}=2\pi-\sum_{i=1}^k\epsilon_i +\int_{\mathbf{x}^{-1}(R)}\left( \frac{\partial Q}{\partial u_1}(u_1,u_2) -\frac{\partial P}{\partial u_2}(u_1,u_2) \right)\,\text{d}u_1\text{d}u_2\\ &{}=2\pi-\sum_{i=1}^k\epsilon_i +\int_{\mathbf{x}^{-1}(R)}(K\circ\mathbf{x})\sqrt{g_{11}g_{22}}\\ &{}=2\pi-\sum_{i=1}^k\epsilon_i +\int_{R}K, \end{aligned} \] que é o que queriamos ver.
Teorema de Gauss-Bonnet global
Sexa $S$ unha supeficie regular orientada.
Para enuncia-lo teorema de Gauss-Bonnet necesitaremos varios preparativos topolóxicos. Introducirémo-las definicións, pero varios dos enunciados non os probaremos neste curso.
Recordemos que unha rexión $R\subset S$ é un conxunto aberto conexo, relativamente compacto de $S$ tal que $\partial R$ é unión dunha cantidade finita de compoñentes conexas cada unha das cales é homeomorfa a $\mathbb{S}^1$, e que pode ser parametrizada regularmente a trozos.
Un triángulo (curvado) de $S$ é unha curva pechada simple regular a trozos $\alpha\colon[a,b]\to S$ na partición $a=t_0<t_1<t_2<t_3=b$, que está contida nunha veciñanza coordenada $\mathbf{x}(U)$ que é homeomorfa a unha bóla. Cada segmento $\alpha_{\vert[t_i,t_{i+1}]}$ chámase arista.
Unha triangulación dunha rexión $R$ é unha familia $\mathcal{T}=\{T_1,\dots,T_k\}$ de rexións contidas en $R$ tal que:
- O borde $\partial T_i$ de cada $T_i$ é un triángulo.
- $\overline{R}=\cup_{i=1}^k\overline{T_i}$.
- Se $i\neq j$ entón $\overline{T_i}\cap\overline{T_j}=\emptyset$ ou $\overline{T_i}\cap\overline{T_j}$ é unha arista ou un vértice común.
Cada un dos $T_i$ da triangulación chámanse caras, cada arista de cada $T_i$ é unha arista da triangulación, e cada vértice de cada $\partial T_i$ é un vértice da triangulación. O número de cada un deles denótase $C$, $A$ e $V$ respectivamente.
Chámase característica de Euler da rexión $R$ (con respecto da triangulación $\mathcal{T}$) a $C-A+V$.
As seguintes interseccións non pertencerían a triangulación válidas, xa que os triángulos non se intersecan correctamente.
As interseccións de triángulos que se amosan non son correctas para unha triangulación.
Os seguintes triángulos si se intersecan correctamente.
As interseccións de triángulos que van a continuación si serían válidas para unha triangulación.
Sexa $R$ unha rexión nunha superficie $S$. Entón:
- $R$ admite unha triangulación.
- A característica de Euler non depende da triangulación escollida.
- A característica de Euler é un invariante topolóxico: se $R$ e $\tilde{R}$ son dúas rexións homeomorfas, entón a súa característica de Euler é a mesma.
En virtude da proposición anterior, a característica de Euler dunha rexión denotarase de xeito non ambiguo por $\chi(R)$.
Calculámo-la característica de Euler dalgunhas rexións. Para iso basta con atopar algunha triangulación da rexión dada, xa que a característica de Euler é a mesma para calquera triangulación.
A característica de Euler dunha rexión simple $R$ é $\chi(R)=1$. En realidade unha rexión simple é homeomorfa a un triángulo e así $C=1$, $A=3$, $V=3$.
A continuación calculámo-la característica de Euler dunha rexión $R$ homeomorfa a un anel circular. Recordemos ademais que unha rexión tal tamén é homeomorfa a un cilindro. Presentamos unha posible triangulación, que non ten por que se-la máis eficiente, pero que é relativamente sinxela de pintar.
Para a triangulación da rexión homeomorfa ó anel circular temos $C=12$, $A=24$, $V=12$. Por tanto, a característica de Euler da rexión é $\chi(R)=0$.
A continuación preséntanse dúas posibles triangulacións da esfera.


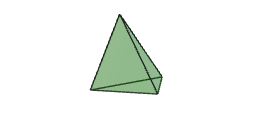
Non obstante, a triangulación máis simple posible da esfera consiste en darse conta de que esta é homeomorfa a un tetraedro. Neste caso temos $C=4$, $A=6$, $V=4$. Por tanto $\chi(\mathbb{S}^2)=2$.
A característica de Euler da esfera é un invariante topolóxico que é coñecido na educación elemental cando se estudian os poliedros.
Finalmente calculámo-la característica de Euler do toro $\mathsf{T}^2$.
Neste caso cómpre ter tino coas interseccións dos triángulos, xa que se tomamos moi poucos non se cumplen os axiomas de triangulación como amosan as figuras adxuntas de triangulacións non válidas do toro.
Recordemos que un toro é homeomorfo ó espacio topolóxico cociente resultante de identificar dous a dous os lados dun cadrado.
A triangulación que se presenta non é a máis eficiente, pero cumple os axiomas de triangulación. Para esta $C=18$, $A=27$, $V=9$, e por tanto, $\chi(\mathsf{T}^2)=0$.
A característica de Euler pode definirse non soamente para triangulacións, senón para calquera subdivisión en polígonos, non necesariamente todos cos mesmos lados, sempre e cando se cumpla a condición de que ou non se intersecan, ou se intersecan en todo un lado ou nun vértice. Para ver isto, basta con subdividi-los polígonos en triángulos e ver que na nova subdivisión se cancelan as sumas.
No anuncio adxunto preséntase unha subdivisión da esfera en hexágonos, o cal é imposible desde o punto de vista topolóxico se se preserva a regularidade nas subdivisións que se ve na parte visible do balón. Se $C$ é o número de hexágonos, o número de aristas é $A=6C/2$, xa que cada hexaedro ten $6$ aristas pero a mesma arista está compartida por dúas caras, e o número de vértices é $V=6C/3$, xa que cada hexaedro ten $6$ vértices pero cada vértice está compartido por $3$ caras. En total, teriamos que a característica de Euler da esfera sería \[ \chi(\mathbb{S}^2)=C-6C/2+6C/3=0, \] o que é imposible.
Sexa $S$ unha superficie regular compacta, conexa, e orientable. Entón:
- A característica de Euler de $S$ é $2$ (esfera), $0$ (toro), $-2$ (2-toro), $-4$ (3-toro), …, $-2n+2$ (n-toro).
- Se $\tilde{S}$ é outra superficie compacta, conexa, e orientable, entón $S$ é homeomorfa a $\tilde{S}$ se e só se $\chi(S)=\chi(\tilde{S})$.
Tamén se chama xénero dunha superficie compacta, conexa, e orientable ó número de buratos, é dicir, $g(S)=\frac{2-\chi(S)}{2}$, que por tanto tamén serve para clasificalas topoloxicamente.
Concretamente, se $S$ é compacta, conexa, e orientable, entón $g(S)=0,1,2,\dots$ e $S$ é homeomorfa a:
- Unha esfera se $g(S)=0$.
- Un n-toro se $g(S)>0$.

Sexa $S$ unha superficie orientada e $R\subset S$ unha rexión. Entón:
- Existe unha familia de parametrizacións ortogonais e positivamente orientadas $\mathbf{x}^i\colon U_i\subset\R^2\to S$ que recubren $S$, sendo cada $U_i$ homeomorfo a unha bóla de $\R^2$.
- Existe unha triangulación $\mathcal{T}=\{T_1,\dots, T_k\}$ de $S$ tal que cada triángulo $T_i$ está contido nalgunha das veciñanzas coordenadas $\mathbf{x}^j(U_j)$.
Por tanto, dada unha rexión $R$ dunha superficie orientada $S$, escolleremos unha triangulación $\mathcal{T}=\{T_1,\dots,T_k\}$ nas condicións anteriores. Nese caso tomaremos en cada $\partial T_i$ a orientación positiva (dentro de $\mathbf{x}^j(U_j)$).
A observación clave que necesitamos facer agora é que cando dous triángulos contidos nun aberto coordenado como o anterior teñen unha arista en común, a orientación de dita arista como arista dun dos triángulos será oposta á orientación desa arista como arista do triángulo contiguo.
Nestas condicións dámoslle ó borde a orientación inducida pola orientación dos triángulos da triangulación.
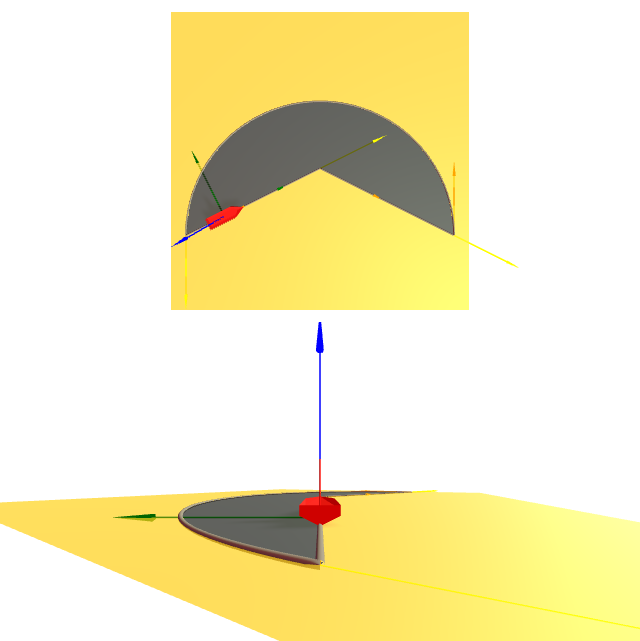
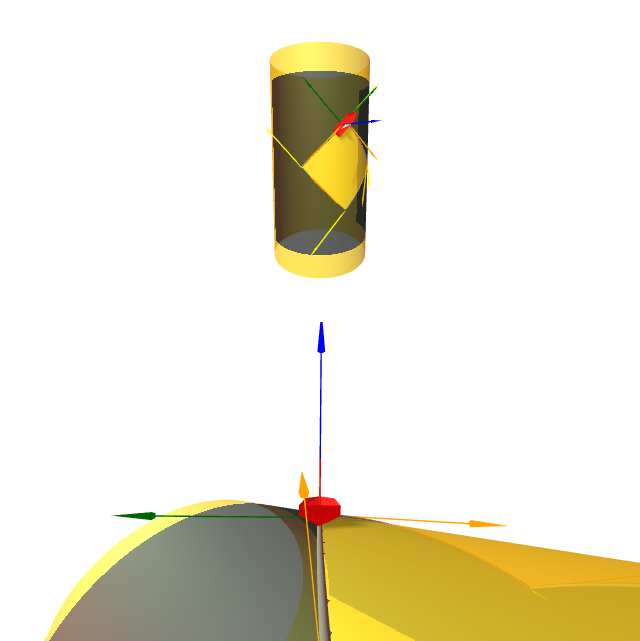
Recordemos que, intuitivamente, o borde dunha rexión está orientado positivamente cando ó mirar cara á superficie con vector normal apuntando cara nós, o borde percórrese de xeito que a rexión queda do lado esquerdo.
Na gráfica preséntase unha rexión que non é simple, pero fixémonos que co vector normal saínte o vehículo recorre o borde deixando a rexión gris á súa esquerda, tanto para o borde exterior (recorrido en sentido antihorario segundo se mira) como para o interior (recorrido en sentido horario segundo se mira).
Sexa $S$ unha superficie regular orientada e $R$ unha rexión con fronteira $\partial R$ positivamente orientada. Entón, \[ \int_R K+\int_{\partial R}\kappa_g+\sum_{i=1}^k\epsilon_i=2\pi\chi(R), \] onde $\epsilon_1,\dots,\epsilon_k$ son os ángulos exteriores nos vértices de $\partial R$.
Sexa $\mathcal{T}=\{T_1,\dots,T_C\}$ unha triangulación da rexión $R$ de xeito que cada $T_i$ está contido nunha veciñanza coordenada ortogonal, positivamente orientada e homeomorfa a unha bóla. Denotamos por $C$ ó número de caras, por $A$ ó número de aristas, e por $V$ ó número de vértices.
Pola versión local do teorema de Gauss-Bonnet para cada triángulo, temos \[ \int_{T_i}K+\sum_{j=1}^3\int_{\alpha_{ij}}\kappa_g +\sum_{j=1}^3\epsilon_j^i=2\pi, \] onde $\{\epsilon_1^i,\epsilon_2^i,\epsilon_3^i\}$ son os ángulos exteriores do triángulo $\partial T_i$, e $\alpha_{ij}$ son os lados de $\partial T_i$.
Como $\overline{R}=\cup_{i=1}^C \overline{T_i}$, e $\overline{T_i}\cap\overline{T_j}$ ten medida cero con $i\neq j$, sumando obtemos \[ \begin{aligned} 2\pi C &{}=\sum_{i=1}^C\left( \int_{T_i}K+\sum_{j=1}^3\int_{\alpha_{ij}}\kappa_g+\sum_{j=1}^3\epsilon_j^i \right)\\ &{}=\int_R K+\sum_{i=1}^C\sum_{j=1}^3\int_{\alpha_{ij}}\kappa_g +\sum_{i=1}^C\sum_{j=1}^3\epsilon_j^i. \end{aligned} \]
A continuación calculamos por separado os dous sumandos da expresión anterior que quedan por determinar.
En primeiro lugar empezamos coa integral da curvatura xeodésica nas aristas da triangulación. O que segue é un argumento combinatorio no que separámo-la suma en dúas partes: a suma das integrais da curvatura xeodésica das aristas que son interiores, e a correspondente suma das aristas que están no borde. Recordemos que as aristas interiores se percorren en sentidos opostos en triángulos contiguos, así que as integrais das súas curvaturas xeodésicas se cancelan dúas a dúas. Entón, \[ \begin{aligned} \sum_{i=1}^C\sum_{j=1}^3\int_{\alpha_{ij}}\kappa_g &{}=\sum_{\stackrel{i,j}{\text{$\alpha_{ij}$ interior}}}\int_{\alpha_{ij}}\kappa_g +\sum_{\stackrel{i,j}{\text{$\alpha_{ij}$ no borde}}}\int_{\alpha_{ij}}\kappa_g\\[1ex] &{}=\int_{\partial R}\kappa_g. \end{aligned} \]
Fixámonos agora na suma dos ángulos exteriores nos vértices dos triángulos da triangulación.
Un vértice de $\mathcal{T}$ pode estar no borde de $R$ ou ser interior. Denotamos, respectivamente, o seu número por $V_{ext}$ e $V_{int}$. Por tanto, $V=V_{ext}+V_{int}$. Observamos que se $\epsilon_j^i$ denota o ángulo exterior no vértice dun triángulo, entón $\pi-\epsilon_j^i$ será o ángulo interior nese vértice. Ademais, se o vértice é interior á rexión, entón a suma de tódolos ángulos interiores que conflúen nese vértice ten que ser $2\pi$.
Analogamente, unha arista pode estar no borde ou non. Ó seu número respectivo denotarémolo por $A_{ext}$ e $A_{int}$. Así $A=A_{ext}+A_{int}$.
Empezámo-lo cálculo da suma dos ángulos nos vértices: \[ \begin{aligned} \sum_{i=1}^C\sum_{j=1}^3\epsilon_j^i &{}=\sum_{i=1}^C\sum_{j=1}^3(\pi-\pi+\epsilon_j^i)\\ &{}=3\pi C-\sum_{i=1}^C\sum_{j=1}^3(\pi-\epsilon_j^i)\\ &{}=3\pi C -\sum_{\stackrel{i,j}{\text{interior}}}(\pi-\epsilon_j^i) -\sum_{\stackrel{i,j}{\text{no borde}}}(\pi-\epsilon_j^i)\\ &{}=3\pi C-2\pi V_{int} -\sum_{\stackrel{i,j}{\text{no borde}}}(\pi-\epsilon_j^i). \end{aligned} \]
Os vértices do borde á súa vez dividirémolos en dúas familias disxuntas. Por un lado, denotemos por $\sigma$ ó conxunto de vértices de $\partial R$. Estes son os $k$ vértices orixinais do enunciado nos que temos os ángulos exteriores $\epsilon_1,\dots,\epsilon_k$. Por outra lado, sexa $\tau$ o conxunto dos vértices que están en $\partial R$ pero que foron introducidos pola triangulación (é dicir, que en realidade, como puntos de $\partial R$ son regulares). Ó número de todos eles denotarémolo por $\lvert\tau\rvert$. Obviamente tamén temos $V_{ext}=k+\lvert\tau\rvert$, xa que $\sigma$ e $\tau$ teñen como unión (disxunta) o conxunto de tódolos vértices que están $\partial R$.
Agora hai que ter en conta que nos vértices do borde que foron introducidos pola tringulación o ángulo que temos é chan porque estamos en puntos de regularidade da parametrización do borde, así que a suma dos ángulos interiores nese vértice é $\pi$.
Consideremos agora un vértice orixinal de $\partial R$, con ángulo exterior $\epsilon_\alpha$. Sexa $\sigma_\alpha$ o conxunto dos ángulos interiores nese vértice de triángulos de $\mathcal{T}$. Obviamente, o ángulo interior de $\partial R$ nese vértice coincide coa suma de tódolos ángulos interiores de triángulos que conflúen nese vértice, é dicir, \[ \pi-\epsilon_\alpha =\sum_{\stackrel{i,j}{\text{en $\sigma_\alpha$}}}(\pi-\epsilon_j^i). \] Sumando en tódolos vértices de $\partial R$ e despexando obtemos \[ \sum_{\stackrel{i,j}{\text{en $\sigma$}}}(\pi-\epsilon_j^i) =\pi k-\sum_{i=1}^k\epsilon_i. \]
Continuando co cálculo anterior, \[ \begin{aligned} \sum_{i=1}^C\sum_{j=1}^3\epsilon_j^i &{}=3\pi C-2\pi V_{int} -\sum_{\stackrel{i,j}{\text{en $\sigma$}}}(\pi-\epsilon_j^i) -\sum_{\stackrel{i,j}{\text{en $\tau$}}}(\pi-\epsilon_j^i)\\ &{}=3\pi C-2\pi V_{int} -\pi k+\sum_{i=1}^k\epsilon_i -\pi\lvert\tau\rvert\\ &{}=3\pi C-2\pi V_{int}-\pi V_{ext}+\sum_{i=1}^k\epsilon_i\\ \end{aligned} \]
Agora témo-la seguinte relación: \[ 3C=2A_{int}+A_{ext}. \] En efecto, pois cada cara ten exactamente 3 aristas, cada arista interior está compartida por exactamente 2 triángulos, e cada arista non interior está exactamente nun triángulo.
Observamos tamén que o número de vértices exteriores está en correspondencia un a un co número de aristas exteriores (a correspondencia asígnalle a cada arista o vértice onde empeza): \[ \begin{aligned} \sum_{i=1}^C\sum_{j=1}^3\epsilon_j^i &{}=\pi(2A_{int}+A_{ext})-2\pi V_{int}-\pi V_{ext}+\sum_{i=1}^k\epsilon_i\\ &{}=2\pi A_{int}+\pi A_{ext} -2\pi V_{int}-2\pi V_{ext}+\pi V_{ext}+\sum_{i=1}^k\epsilon_i\\ &{}=2\pi A_{int}+\pi A_{ext} -2\pi V+\pi A_{ext}+\sum_{i=1}^k\epsilon_i\\ &{}=2\pi A-2\pi V+\sum_{i=1}^k\epsilon_i. \end{aligned} \]
Substituíndo, \[ \begin{aligned} 2\pi C &{}=\int_R K+\int_{\partial R}\kappa_g +2\pi A-2\pi V+\sum_{i=1}^k\epsilon_i, \end{aligned} \] e despexando obtense a fórmula de Gauss-Bonnet global \[ \begin{aligned} \int_R K+\int_{\partial R}\kappa_g +\sum_{i=1}^k\epsilon_i &{}=2\pi C-2\pi A+2\pi V\\ &{}=2\pi\chi(R), \end{aligned} \] como queriamos ver.
Sexa $S$ unha superficie compacta orientable. Entón, \[ \int_S K = 2\pi\chi(S). \]
Simplemente hai que observar que para a fórmula global de Gauss-Bonnet neste caso non hai borde. A demostración tamén se pode ver como un caso máis sinxelo da anterior xa que o argumento pode repetirse tendo en conta que tódolos vértices e tódalas aristas son interiores.
Consecuencias dos teoremas de Gauss-Bonnet
Hai multitude de consecuencias xeométricas para o teorema de Gauss-Bonnet. A continuación presentamos soamente algunhas delas.
Unha superficie regular conexa, compacta, orientada, de curvatura positiva é homeomorfa a unha esfera.
Como $K>0$, temos $0<\int_S K=2\pi\chi(S)$, co que $\chi(S)>0$. Isto só é posible con $\chi(S)=2$ e sendo $S$ unha esfera de acordo co teorema que nos dá as características de Euler das superficies compactas orientables.
Sexa $S$ unha superficie regular conexa, compacta, orientada, e con curvatura de Gauss positiva. Entón dúas xeodésicas pechadas e simples calquera córtanse.
Sexan $\gamma_1$ e $\gamma_2$ dúas xeodésicas pechadas e simples que non se cortan. Como $S$ é conexa, compacta, e de curvatura positiva, obtemos que $S$ é homeomorfa a unha esfera. Logo, $\gamma_1$ e $\gamma_2$ determinan unha rexión $R$ en $S$ que é homeomorfa a unha coroa circular. Por tanto $\chi(R)=0$. Ademais, o borde é regular e formado por xeodésicas. Pola fórmula de Gauss-Bonnet obtemos $\int_R K=0$, o que contradí $K>0$.
Sexa $S$ unha superficie con curvatura negativa. Se dúas xeodésicas $\gamma_1$ e $\gamma_2$ se cortan en dous puntos distintos, a rexión que determinan non é simple.
Supoñamos que $S$ é unha superficie que satisfai $K<0$ en todo punto. Sexan $\gamma_1\colon[a_1,b_1]\to S$, e $\gamma_2\colon[a_2,b_2]\to S$, dúas xeodésicas que se cortan en dous puntos distintos $\gamma_1(a_1)=\gamma_2(a_2)$, $\gamma_1(b_1)=\gamma_2(b_2)$.
Considerémo-la rexión $R$ encerrada por $\gamma_1$ e $\gamma_2$. Denotamos por $\epsilon_1$ e $\epsilon_2$ os ángulos exteriores nos puntos de corte $\gamma_1(a_1)=\gamma_2(a_2)$, $\gamma_1(b_1)=\gamma_2(b_2)$ respectivamente. Nótese que $\epsilon_i\neq\pm\pi$, pois noutro caso, serían reparametrizacións da mesma xeodésica.
Pola fórmula de Gauss-Bonnet, \[ \begin{aligned} 2\pi\chi(R) &{}=\int_R K+\int_{\partial R}\kappa_g+\epsilon_1+\epsilon_2\\[1ex] &{}< \epsilon_1+\epsilon_2 < \pi+\pi =2\pi, \end{aligned} \] co que $\chi(R)\neq 1$. Como as rexión simples teñen característica de Euler igual a 1, chegamos a unha contradicción, e por tanto, $R$ non é simple.
Recordemos que a curvatura negativa afasta as xeodésicas (suficientemente preto dun punto), pero por cuestións topolóxicas, estas xeodésicas poden volver a atoparse.
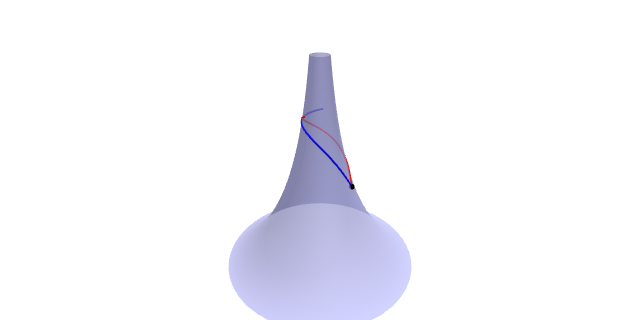
A suma dos ángulos interiores dun triángulo xeodésico nunha superficie chá é $\pi$.
Sexa $T$ é un triángulo tal que os seus lados son xeodésicas. Sexan $\epsilon_1$, $\epsilon_2$ e $\epsilon_3$ os ángulos exteriores e $\varphi_i=\pi-\epsilon_i$ os ángulos interiores. Como $K=0$ e $\kappa_g=0$ en $\partial T$, e $\chi(T)=1$, o teorema de Gauss-Bonnet di \[ \begin{aligned} 2\pi=2\pi\chi(T) &{}=\int_T K+\int_{\partial T}\kappa_g+\epsilon_1+\epsilon_2+\epsilon_3\\ &{}=3\pi-(\varphi_1+\varphi_2+\varphi_3), \end{aligned} \] de onde se deduce $\varphi_1+\varphi_2+\varphi_3=\pi$.
Coa mesma conta:
- En xeometría esférica a suma dos ángulos interiores dun triángulo é maior ca $\pi$.
- En xeometría hiperbólica a suma dos ángulos interiores dun triángulo é menor ca $\pi$.

