Repaso de curvas e superficies
Curvas parametrizadas
Unha curva parametrizada regular é unha aplicación diferenciable $\alpha\colon I\to \R^n$ tal que $\alpha'(t)\neq \mathbf{0}$. Por "diferenciable" entenderemos sempre "infinitamente diferenciable". Se $n=2$ diremos que a curva é plana. Neste curso centrarémonos en curvas no espacio, $n=3$.
A integral de liña de $f\colon I\to \R$ ó longo da curva $\alpha\colon I\to \R^n$ defínese como \[ \int_\alpha f=\int_I f(t)\lVert\alpha'(t)\rVert\,\textup{d}t. \] Tomando $f=1$, témo-la lonxitude dun anaco dunha curva: \[ L(\alpha)=\int_I\,\lVert\alpha'\rVert. \]
Toda curva parametrizada regular pode ser reparametrizada polo parámetro lonxitude de arco, denotado por $s$, de xeito que $\lVert\alpha'(s)\rVert=1$ para todo $s$ onde está definida. O parámetro lonxitude de arco consíguese mediante o cambio de variable $s(t)=\int_{t_0}^t\lVert\alpha'(u)\rVert\,\textup{d}u$.
Supoñamos que $\alpha$ está parametrizada por arco. Defínese o vector tanxente a $\alpha$ como \[ \mathbf{t}(s)=\alpha'(s). \] A curvatura de $\alpha$ é \[ \kappa(s)=\lVert\alpha''(s)\rVert=\lVert\mathbf{t}'(s)\rVert. \] O vector normal defínese como \[ \mathbf{n}(s)=\frac{\alpha''(s)}{\lVert\alpha''(s)\rVert} =\frac{\mathbf{t}'(s)}{\kappa(s)}. \] O vector binormal simplemente completa ó tanxente é ó normal para obter unha base ortonormal de $\R^3$ mediante \[ \mathbf{b}(s)=\mathbf{t}(s)\times\mathbf{n}(s). \] A base ortonormal $\{\mathbf{t}(s),\mathbf{n}(s),\mathbf{b}(s)\}$ chámase triedro de Frenet. Finalmente, a torsión de $\alpha$ é \[ \tau(s)=\langle\mathbf{n}'(s),\mathbf{b}(s)\rangle. \]
Os conceptos introducidos con anterioridade están relacionados elegantemente mediante as chamadas fórmula de Frenet-Serret: \[ \begin{pmatrix} \mathbf{t}'\\ \mathbf{n}' \\ \mathbf{b}' \end{pmatrix} = \begin{pmatrix} 0 & \kappa & 0\\ -\kappa & 0 &\tau\\ 0 & -\tau & 0 \end{pmatrix} \begin{pmatrix} \mathbf{t}\\ \mathbf{n} \\ \mathbf{b} \end{pmatrix}. \]
En caso de que $\alpha$ non estea parametrizada por arco, as fórmulas xerais para a curvatura e a torsión son \[ \begin{aligned} \kappa &{}= \frac{\lVert\alpha'\times\alpha''\rVert}{\lVert\alpha'\rVert^3},\\[1ex] \tau &{}=\frac{\det(\alpha',\alpha'',\alpha''')} {\lVert\alpha'\times\alpha''\rVert^2}. \end{aligned} \]
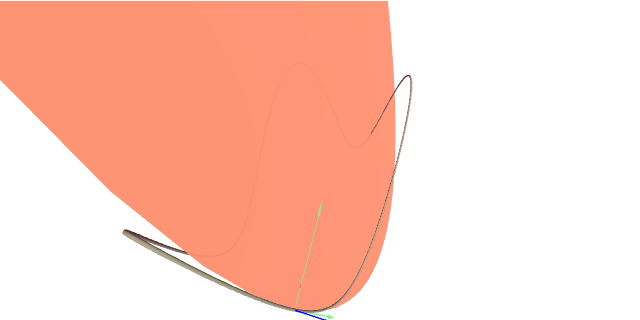
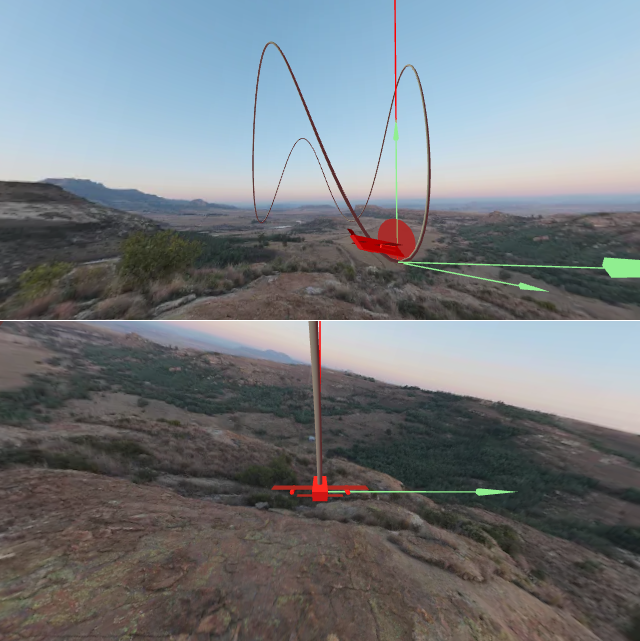
Nos seguintes gráficos preséntase o triedro de Frenet dunha curva mediante vectores verdes. A curvatura está representada mediante un vector vermello na dirección do normal, e a torsión mediante un vector azul na dirección do binormal. Recordemos que a curvatura representa como de rapidamente cambia o vector tanxente da curva, mentres que a torsión representa como de rápido cambia o plano osculador á curva, que é aquel xenerado polo vector tanxente e o vector normal en cada punto.
Nos gráficos tamén se representa o círculo osculador. Este é un círculo contido no plano osculador, que é tanxente á curva no punto dado, e que ten a mesma curvatura cá curva nese punto. Por así dicilo, o círculo osculador é o círculo que mellor aproxima á curva no punto dado. O seu radio $R(s)=1/\kappa(s)$ chámase radio de curvatura, que habitualmente se emprega na física en lugar da curvatura para expresa-la aceleración normal.
Superficies regulares
A continuación recordamos algunhas nocións preliminares de superficies no espacio.
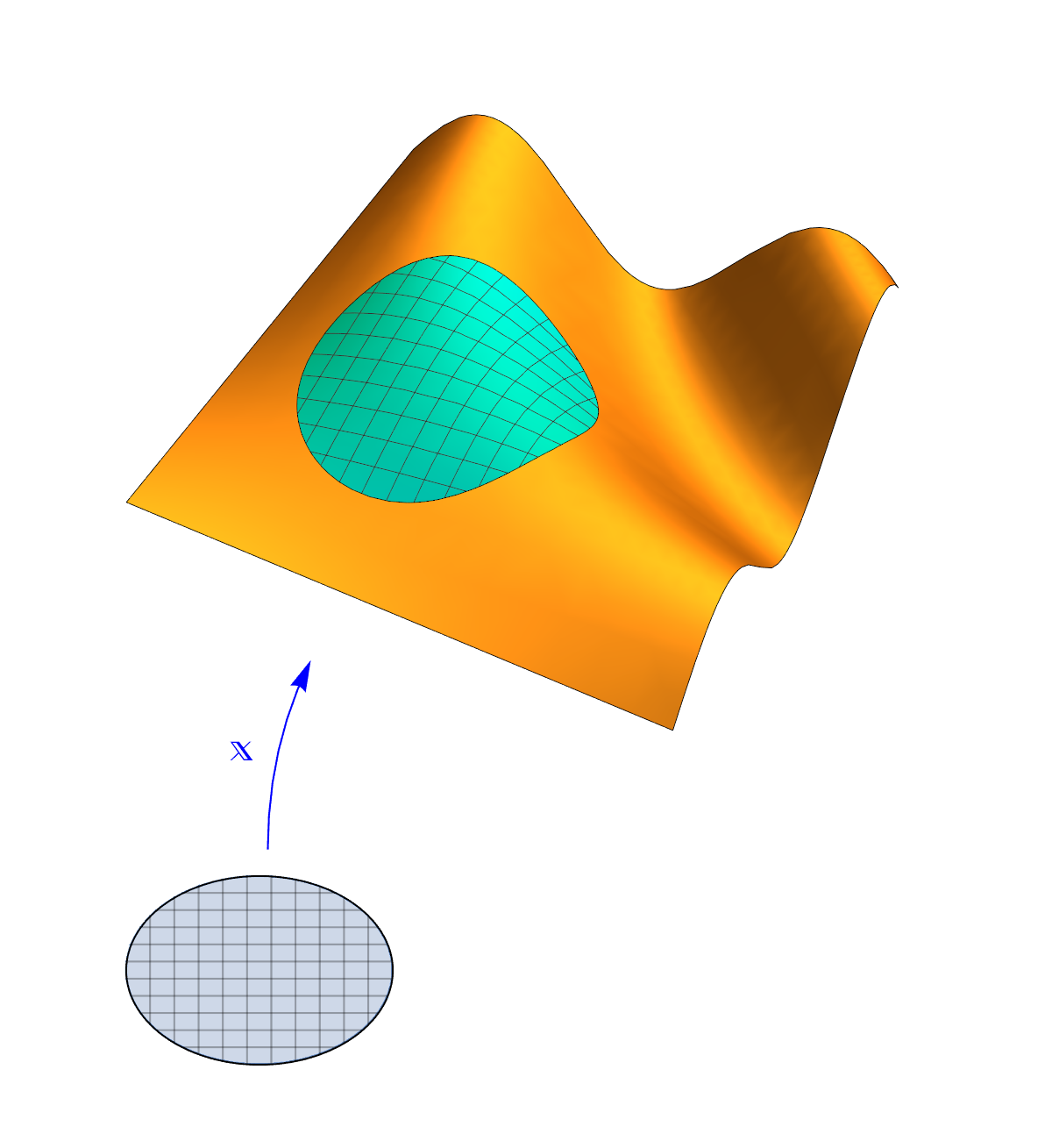
Unha superficie regular $S$ é un subconxunto de $\R^n$ tal que para cada punto $p\in S$ existe un aberto $U$ de $\R^2$, unha veciñanza $V$ de $S$ en $p$, e unha aplicación $\mathbf{x}\colon U\to V\subset\R^n$ tales que
- $\mathbf{x}$ é diferenciable.
- $\mathbf{x}\colon U\to \mathbf{x}(U)=V$ é un homeomorfismo.
- A diferencial $d\mathbf{x}_q\colon\R^2\to\R^n$ é inxectiva para todo $q\in U$.
De novo, por "diferenciable" entendemos "infinitamente diferenciable", e neste curso centrarémonos en superficies no espacio, $n=3$.
Á veciñanza $V$ chámaselle unha veciñanza coordenada. Tamén é común chamarlle a $\varphi=\mathbf{x}^{-1}$ unha carta da superficie.
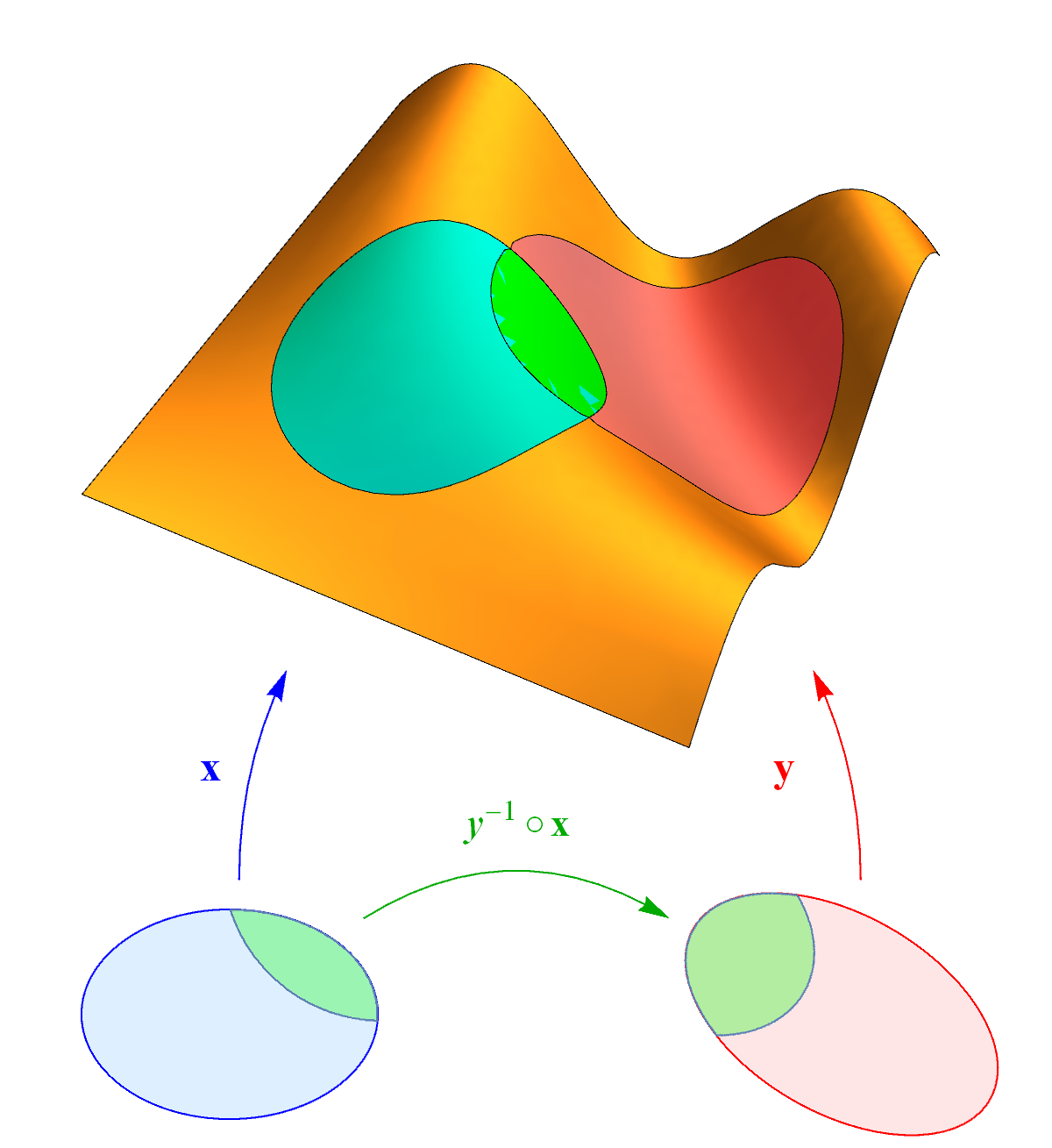
Un resultado fundamental na teoría de superficies é o feito de que, se dúas veciñanzas coordenadas se solapan, entón o cambio de parametrización dunha a outra é diferenciable. Máis concretamente, sexan $\mathbf{x}\colon U\to S$ e $\mathbf{y}\colon V\to S$ dúas parametrizacións tales que $\mathbf{x}(U)\cap\mathbf{y}(V)\neq\emptyset$. Entón, a aplicación \[ \mathbf{y}^{-1}\circ\mathbf{x}\colon \mathbf{x}^{-1}(\mathbf{x}(U)\cap\mathbf{y}(V))\to \mathbf{y}^{-1}(\mathbf{x}(U)\cap\mathbf{y}(V)) \] é diferenciable no sentido ordinario de aplicacións entre abertos de $\R^2$.
A xeometría diferencial de superfices consiste fundamentalmente en atopa-las propiedades dunha superficie que se poden expresar independentemente das súas parametrizacións.
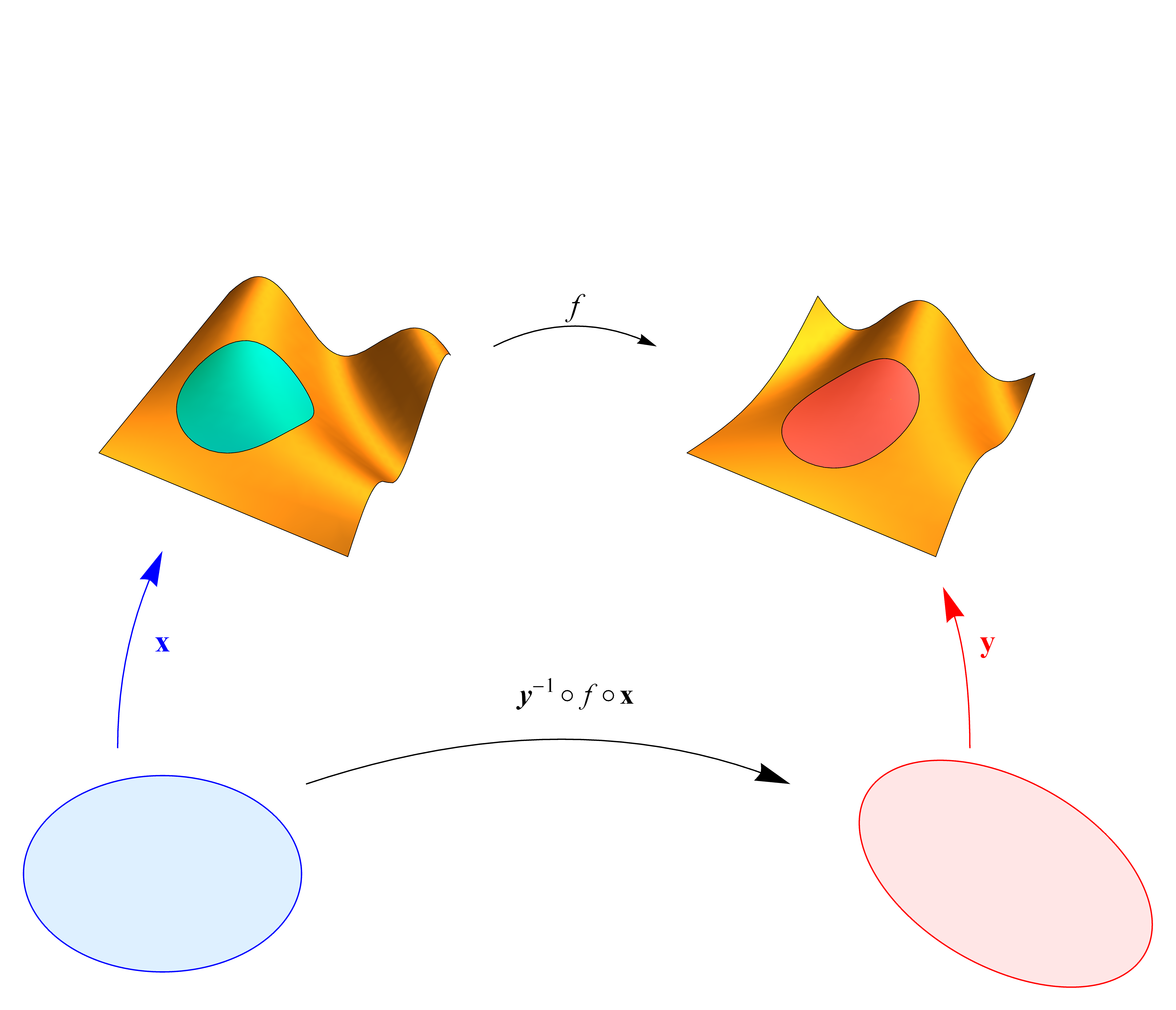
Sexan $S_1$ e $S_2$ dúas superficies regulares. Unha aplicación $f\colon S_1\to S_2$ dise diferenciable en $p\in S_1$ se existen parametrizacións $\mathbf{x}\colon U_1\to S_1$ e $\mathbf{y}\colon U_2\to S_2$ tales que $p\in\mathbf{x}(U_1)$, $f(p)\in\mathbf{y}(U_2)$, e $\mathbf{y}^{-1}\circ f\circ \mathbf{x}$ é diferenciable, no sentido ordinario, en $\mathbf{x}^{-1}(p)$. Dirase que $f$ é diferenciable se o é en tódolos seus puntos.
Pódese comprobar, en virtude do resultado anterior relativo ós cambios de coordenadas, que a diferenciabilidade dunha aplicación non depende das parametrizacións elexidas. O concepto de aplicación diferenciable $f\colon S\to \R^k$ defínese de xeito análogo. A composición de aplicacións diferenciables segue sendo diferenciable, e este resultado segue sendo válido se misturámo-los conceptos de diferenciabilidade habitual co de aplicacións entre superficies.
Dise que unha aplicación $f\colon S_1\to S_2$ é un difeomorfismo se é diferenciable, ten inversa $f^{-1}\colon S_2\to S_1$, e $f^{-1}$ tamén é diferenciable.
Dise que $f\colon S_1\to S_2$ é un difeomorfismo local en $p\in S_1$ se existe unha veciñanza aberta $U$ de $p$ e outra veciñanza aberta $V$ de $S_2$ en $f(p)$ tal que a restricción $f_{\vert U}\colon U\to V$ é un difeomorfismo.
Plano tanxente, vector normal e curvatura de Gauss
Sexa $S$ unha superficie regular e $\mathbf{x}\colon U\to S$ unha parametrización. Será habitual denota-las variables desta aplicación por $(u,v)$, aínda que ás veces a notación $(u_1,u_2)$ será máis convinte para poder facer uso dos subíndices cando haxa sumatorios.
As derivadas de $\mathbf{x}$ con respecto das variables denótanse por $\mathbf{x}_u$ e $\mathbf{x}_v$ (ou $\mathbf{x}_1$, $\mathbf{x}_2$) e chámanse os campos de vectores coordenados.
O plano tanxente a $S$ en $p\in S$, $T_p S$, defínese, de xeito independente das parametrizacións, como o espacio vectorial formado polas velocidades (derivadas) de curvas diferenciables contidas en $S$ pasando por $p$. Non obstante, para unha parametrización $\mathbf{x}\colon U\to S$ tal que $p\in\mathbf{x}(U)$, este pode caracterizarse mediante $T_p S=d\mathbf{x}_{q}(\R^2)$, onde $q=\mathbf{x}^{-1}(p)$. Neste caso $\{\mathbf{x}_1(q),\mathbf{x}_2(q)\}$ é unha base de $T_p S$.
Sexa $f\colon S_1\to S_2$ unha aplicación diferenciable entre superficies. A súa diferencial en $p\in S$ é unha aplicación linear $df_p\colon T_p S_1\to T_{f(p)} S_2$ definida como \[ df_p(v)=(f\circ \alpha)'(0)=\frac{d}{dt}\bigg\vert_{0} f(\alpha(t)), \] onde $\alpha\colon I\to S$ é unha curva con $\alpha(0)=p$, $\alpha'(0)=v$.
A primeira forma fundamental dunha superficie $S$ en $p\in S$ é o producto escalar de $\R^3$ restrixido a $T_p S$, é dicir, $\textup{I}_p\colon T_p S\times T_p S\to \R$, $(v,w)\mapsto\textup{I}_p(v,w)=\langle v, w\rangle$. Para unha parametrización $\mathbf{x}$, defínense os coeficientes da primeira forma fundamental como as funcións \[ g_{ij}(u_1,u_2) =\langle\mathbf{x}_i(u_1,u_2),\mathbf{x}_j(u_1,u_2)\rangle. \] A primeira forma fundamental permite definir, de xeito intrínseco á superficie, a lonxitude de curvas, os ángulos entre vectores tanxentes nun mesmo punto, ou a área dunha rexión nunha superficie.
Unha aplicación $f\colon S_1\to S_2$ entre superficies dise unha isometría local se é diferenciable e $\langle df_p(v),df_p(w)\rangle=\langle v,w\rangle$ para todo $p\in S_1$ e tódolos $v,w\in T_p S_1$. Dito doutro xeito, unha aplicación é unha isometría local se preserva a primeira forma fundamental.
Dise que unha aplicación entre superficies é unha isometría (global) se é un difeomorfismo e unha isometría local.
A integral de superficie dunha función $f\colon U\to \R$ ó longo (da parametrización $\mathbf{x}\colon U\subset\R^2\to S$) dunha superficie $S$ defínese como \[ \begin{aligned} \int_{\mathbf{x}(U)} f &{}=\int_{U} f(u_1,u_2) \lVert\mathbf{x}_1(u_1,u_2)\times\mathbf{x}_2(u_1,u_2)\rVert\, \textup{d}u_1\,\textup{d}u_2\\ &{}=\int_{U} f(u_1,u_2)\sqrt{g_{11}(u_1,u_2)g_{22}(u_1,u_2)-g_{12}(u_1,u_2)^2}\, \textup{d}u_1\,\textup{d}u_2. \end{aligned} \] En particular, tomando $f=1$ recupérase a área da rexión $\mathbf{x}(U)$. Pódese ver, empregando o teorema de cambio de variable, que a definición de integral de superficie non depende da parametrización elexida.
Nótese que para aforrar notación moitas veces escribiremos cousas como \[ \int_S f =\int_{U} f\lVert\mathbf{x}_1\times\mathbf{x}_2\rVert =\int_{U} f\sqrt{g_{11}g_{22}-g_{12}^2}. \]
O vector normal a unha superficie pode definirse soamente cando esta é orientable, cuestión que analizaremos máis detidamente no tema de orientación. Non obstante, podemos a estas alturas facer un estudio local. Dada unha parametrización $\mathbf{x}$, o vector normal ou aplicación de Gauss (asociada a $\mathbf{x})$ é a aplicación $N\colon \mathbf{x}(U)\subset S\to \R^3$ definida como \[ \mathbf{N}(\mathbf{x}(u_1,u_2))= \frac{\mathbf{x}_1(u_1,u_2)\times\mathbf{x}_2(u_1,u_2)} {\lVert\mathbf{x}_1(u_1,u_2)\times\mathbf{x}_2(u_1,u_2)\rVert}. \]
No seguinte gráfico preséntanse o plano tanxente e a aplicación de Gauss dunha superficie.
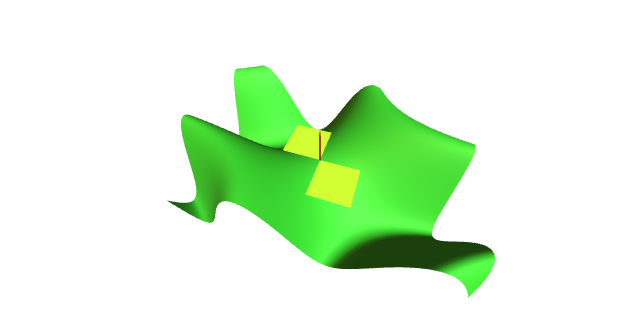
Dado que a aplicación de Gauss ten norma constante igual a un, pode pensarse que a súa imaxe está contida na esfera unidade $\mathbb{S}^2$. Dado un punto $p\in S$, o plano tanxente á esfera no punto $N(p)$ coincide co plano ortogonal a $N(p)$, identificado $N(p)$ cun vector de $\R^3$. En consecuencia, podemos tamén identificar $T_{N(p)}\mathbb{S}^2$ co propio espacio tanxente a $S$ en $p$, $T_p S$.
O operador forma de $S$ en $p\in S$ defínese como a aplicación $A_p\colon T_p S\to T_p S$ dada por \[ A_p(v)=-d\mathbf{N}(p), \] coas identificacións explicadas anteriormente. Pode verse que esta aplicación é autoadxunta con respecto da primeira forma fundamental, e por tanto, o teorema espectral asegura que é diagonalizable con autovalores reais e autoespacios ortogonais. A ditos autovalores chámaselles curvaturas principais. Denotarémolos por $\kappa_1$ e $\kappa_2$, e suporemos $\kappa_1\leq\kappa_2$
A forma cuadrática asociada a $A_p$ chámase segunda forma fundamental, e por tanto, está dada por $\textup{II}_p\colon T_p S\times T_p S\to \R$, $(v,w)\mapsto\textup{II}_p(v,w)=\langle A_p(v),w\rangle$. Dado que $A_p$ é autoadxunto, a segunda forma fundamental é simétrica. Os coeficientes da segunda forma fundamental denótanse por \[ L_{ij}=\langle A\mathbf{x}_i,\mathbf{x}_j\rangle =\langle\mathbf{x}_{ij},\mathbf{N}\circ\mathbf{x}\rangle. \]
Recordemos que un movemento ríxido de $\R^3$ é unha aplicación $F\colon\R^3\to\R^3$ tal que $d(F(p),F(q))=d(p,q)$ para todo $p,q\in\R^3$, e sendo $d$ a distancia euclidiana de $\R^3$. Dise que dúas superficies $S_1$ e $S_2$ son congruentes se existe un movemento ríxido $F\colon\R^3\to\R^3$ tal que $F(S_1)=S_2$. Informalmente, dúas superficies congruentes teñen a mesma primeira e segunda forma fundamentais.
Se $F\colon\R^3\to\R^3$ é un movemento ríxido e $S$ é unha superficie, entón $F_{\vert S}\colon S\to F(S)\subset\R^3$ é unha isometría global de $S$ en $F(S)$. Dúas superficies congruentes son isométricas, pero o recíproco non ten por que ser certo.
A curvatura de Gauss de $S$ en $p$ é \[ \begin{aligned} K(p) &{}=\det d\mathbf{N}_p\\[1ex] &{}=\det A_p=\kappa_1(p)\kappa_2(p), \end{aligned} \] e pode expresarse mediante a primeira e a segunda formas fundamentais como \[ K\circ\mathbf{x}=\frac{L_{11} L_{22}-L_{12}^2}{g_{11}g_{22}-g_{12}^2}. \]
No gráfico seguinte preséntase o plano tanxente e o vector normal a unha superficie que está coloreada de acordo á súa curvatura de Gauss. As tonalidades de vermello expresan o feito de que a curvatura de Gauss é positiva, as tonalidades azuis expresan curvatura negativa, e o branco expresa curvatura cero.

Aínda que de menos importancia nesta materia, tamén empregarémo-la curvatura media definida como \[ \begin{aligned} H(p) &{}=\frac{1}{2}\tr A_p =-\frac{1}{2}\tr\, d\mathbf{N}_p\\[1ex] &{}=\frac{1}{2}\bigl(\kappa_1(p)+\kappa_2(p)\bigr). \end{aligned} \] En coordenadas locais a curvatura media pode expresarse así: \[ H\circ\mathbf{x}=\frac{1}{2}\frac{L_{11}g_{22}+L_{22}g_{11}-2L_{12}g_{12}}{g_{11}g_{22}-g_{12}^2}. \]
Recórdense algúns resultados relativos á curvatura de Gauss e á posición do plano tanxente: se a curvatura de Gauss é positiva, o plano tanxente está (localmente) todo a un lado da superficie, mentres que se a curvatura é negativa, terá puntos da superficie ós dous lados.
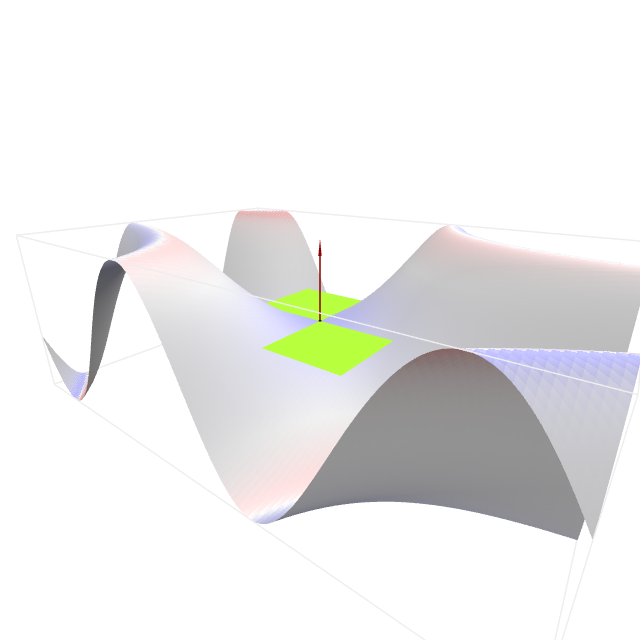
Neste cadro preséntanse varios exemplos de superficies coloreadas de acordo á súa curvatura de Gauss. Pódese anima-lo seu plano tanxente e o seu vector normal.
Fai click e selecciona unha superficie:
A continuación presentamos un dos teoremas máis importantes da teoría de superficies: a curvatura de Gauss é un invariante intrínseco, é dicir, é invariante por isometrías locais entre superficies.
Sexa $f\colon S_1\to S_2$ unha isometría local entre superficies. Entón as curvaturas de Gauss satisfán $K_1(p)=K_2(f(p))$, sendo $K_i$ a curvatura de Gauss de $S_i$.
A demostración do teorema egregium consiste basicamente en escribi-la curvatura de Gauss en termos dos coeficientes da primeira forma fundamental. Para iso empézase por escribir, \[ \mathbf{x}_{ij}=\sum_k \Gamma_{ij}^k\mathbf{x}_k +L_{ij}(\mathbf{N}\circ\mathbf{x}). \] Ós coeficientes $\Gamma_{ij}^k$ chámaselles símbolos de Christoffel, e pódese ver que de feito non dependen máis que da primeira forma fundamental: \[ \Gamma_{ij}^k=\frac{1}{2}\sum_l g^{kl}\left( \frac{\partial g_{jl}}{\partial u_i} +\frac{\partial g_{il}}{\partial u_j} -\frac{\partial g_{ij}}{\partial u_l}\right). \]
A partir de aquí úsase a simetría das segundas derivadas para probar
A curvatura de Gauss e a segunda forma fundamental satisfán:
- Ecuación de Gauss: \[ K=\frac{1}{g_{11}}\left( \frac{\partial \Gamma_{11}^2}{\partial u_2} -\frac{\partial \Gamma_{12}^2}{\partial u_1} +\Gamma_{11}^1\Gamma_{12}^2 +\Gamma_{11}^2\Gamma_{22}^2 -\Gamma_{12}^1\Gamma_{11}^2 -(\Gamma_{12}^2)^2 \right). \]
- Ecuacións de Codazzi-Mainardi: \[ \begin{aligned} \frac{\partial L_{11}}{\partial u_2}-\frac{\partial L_{12}}{\partial u_1} &{}=L_{11}\Gamma_{12}^1+L_{12}(\Gamma_{12}^2-\Gamma_{11}^1) -L_{22}\Gamma_{11}^2,\\ \frac{\partial L_{12}}{\partial u_2}-\frac{\partial L_{22}}{\partial u_1} &{}=L_{11}\Gamma_{22}^1+L_{12}(\Gamma_{22}^2-\Gamma_{12}^1) -L_{22}\Gamma_{12}^2. \end{aligned} \]
De feito, a primeira e segunda forma fundamentais, xunto con estas ecuacións, no sentido que se precisa continuación, determinan unha superficie.
Consideremos funcións diferenciables $g_{ij},L_{ij}\colon U\to\R$, $i,j\in\{1,2\}$, sendo $U$ aberto de $\R^2$, satisfacendo $g_{11}>0$, $g_{22}> 0$, $g_{11}g_{22}-g_{12}^2>0$, e as ecuacións de Gauss e de Codazzi-Mainardi. Entón existe un aberto $\tilde{U}\subset U$ e un difeomorfismo $\mathbf{x}\colon\tilde{U}\to\mathbf{x}(\tilde{U})\subset\R^3$ de xeito que $\mathbf{x}(\tilde{U})$ é unha superficie regular parametrizada por $\mathbf{x}$, e sendo $g_{ij}$ e $L_{ij}$ os coeficientes da súa primeira e segunda forma fundamental, respectivamente.
Ademais, se $\tilde{U}$ é conexo e $\mathbf{y}\colon\tilde{U}\to\mathbf{y}(\tilde{U})$ é outro difeomorfismo que satisfai as condicións anteriores, entón existe un movemento ríxido $F$ de $\R^3$ tal que $\mathbf{y}=F\circ\mathbf{x}$.