A aplicación exponencial
A aplicación exponencial
Sexa $S$ unha superficie regular e $p\in S$.
Dado $v\in T_p S$ sabemos que existe unha única xeodésica maximal $\gamma_v\colon I_v\to S$ tal que $\gamma_v(0)=p$, $\gamma_v'(0)=v$. En principio, $I_v$ non ten por que ser todo $\R$ e pode suceder que $1\in I_v$ ou que non. Denotamos $\mathcal{D}_p=\{v\in T_p S:1\in I_v\}$.
Sexa $S$ superficie regular e $\gamma_v\colon I_v\to S$ xeodésica maximal de $S$ con $\gamma_v(0)=p\in S$ e $\gamma_v'(0)=v\in T_p S$. Sexa $\lambda\in\R$, $\lambda\neq 0$. Se $(-\epsilon,\epsilon)\subset I_v$, entón $(-\epsilon/\lvert\lambda\rvert,\epsilon/\lvert\lambda\rvert)\subset I_{\lambda v}$ e $\gamma_{\lambda v}(t)=\gamma_v(\lambda t)$ para todo $t\in(-\epsilon/\lvert\lambda\rvert,\epsilon/\lvert\lambda\rvert)$.
Sexa $\beta(t)=\gamma_v(\lambda t)$. Temos $\beta(0)=\gamma_v(0)=p$, $\beta'(t)=\lambda\gamma_v'(\lambda t)$, $\beta'(0)=\lambda\gamma_v'(0)=\lambda v$, e \[ \frac{D\beta'}{dt}(t) =\lambda^2\frac{D\gamma_v'}{dt}(\lambda t)=0. \] En consecuencia, $\beta=\gamma_{\lambda v}$, como queriamos ver.
Defínese a aplicación exponencial de $S$ en $p$ como $\exp_p\colon \mathcal{D}_p\subset T_p S\to S$ dada por \[ \exp_p(v)=\gamma_v(1), \] sendo $\gamma_v$ a xeodésica maximal tal que $\gamma_v(0)=p$ e $\gamma_v'(0)=v$.

Utilizando a expresión das xeodésicas do tema anterior temos:
- Se $S$ é un plano entón \[ \exp_p(v)=p+v. \]
- Na esfera $\mathbb{S}(r)$ de radio $r$, \[ \exp_p(v) =\cos\left(\frac{\lVert v\rVert}{r}\right)p +\frac{r}{\lVert v\rVert}\sin\left(\frac{\lVert v\rVert}{r}\right)v. \]
A aplicación exponencial satisfai:
- $\mathcal{D}_p$ é un aberto estrelado con respecto á orixe.
- $\exp_p$ é diferenciable.
- $\gamma_v(t)=\exp_p(tv)$ é a xeodésica maximal tal que $\gamma_v(0)=p$ e $\gamma_v'(0)=v$.
- $\exp_p$ é un difeomorfismo local en $p$.
O feito de que $\mathcal{D}_p$ é aberto e que $\exp_p$ é diferenciable é consecuencia da dependencia diferenciable da solución xeral dunha ecuación diferencial ordinaria con respecto das condicións iniciais. O carácter estrelado de $\mathcal{D}_p$ é consecuencia do lema de homoxeneidade para as xeodésicas, que ademais implica \[ \exp_p(tv)=\gamma_{tv}(1)=\gamma_v(t). \]
A continuación calculamos $\textup{d}\exp_p\colon T_{\mathbf{0}}T_p S\equiv T_p S\to T_p S$. En efecto, \[ \begin{aligned} \textup{d}\exp_p(v) &{}=\frac{d}{dt}\Big\vert_0\exp_p(tv)\\ &{}=\frac{d}{dt}\Big\vert_0\gamma_v(t)\\[1ex] &{}=\gamma_v'(0)=v. \end{aligned} \] Polo teorema da función inversa obtemos entón que $\exp_p$ é un difeomorfismo nunha veciñanza de $p$.
Á xeodésica $t\mapsto \exp_p(tv)$ chámaselle xeodésica radial partindo de $p$ con dirección $v\in T_p S$.
Sexa $U$ unha veciñanza de $p$ estrelada con respecto a $\mathbf{0}\in T_p S$ tal que $\exp_p\colon U\to \exp_p(U)\subset S$ é un difeomorfismo. Tomemos $\{e_1,e_2\}$ unha base ortonormal de $T_p S$. Entón $\mathbf{x}\colon U\to S$, $\mathbf{x}(u_1,u_2)=\exp_p(u_1e_1+u_2e_2)$ é unha parametrización de $S$. Estas coordenadas chámanse coordenadas normais de $S$ en $p$ (asociadas á veciñanza $U$ e á base $\{e_1,e_2\}$). A $V_p=\exp_p(U)$ chámaselle unha veciñanza normal de $S$ en $p$.
Como $U$ é unha veciñanza da orixe en $T_p S$ existe $R>0$ tal que $B_{T_p S}(0,R)\subset U$.
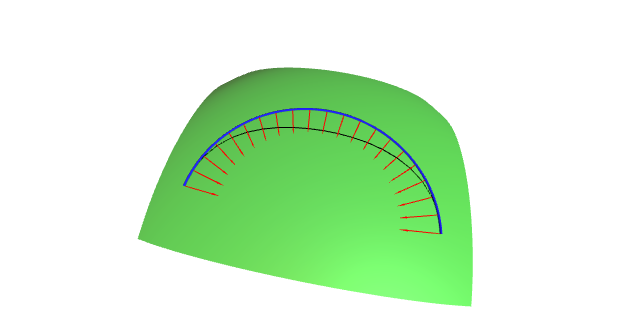
Se $0<r<R$ defínese a bóla xeodésica de centro $p$ e radio $r$ como \[ B_r(p)=\exp_p(B_{T_p S}(0, r)), \] e a circunferencia xeodésica de centro $p$ e radio $r$ como \[ S_r(p)=\exp_p(\partial B_{T_p S}(0,r)). \]

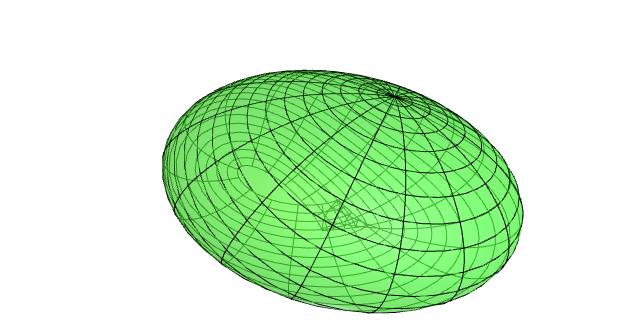
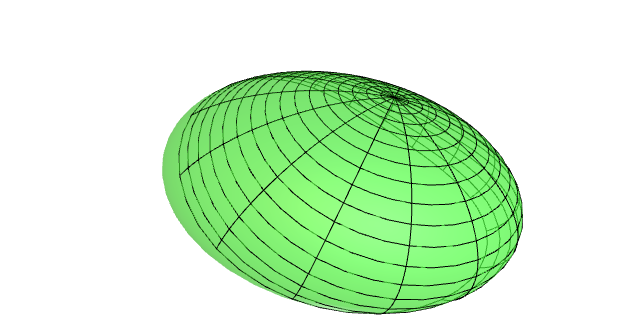
Nótese que nas figuras se ve que a aplicación exponencial non ten por que ser un difeomorfismo global.
Coordenadas polares xeodésicas
Sexa $S$ unha superficie regular, $p\in S$, e $U$ unha veciñanza aberta da orixe de $T_p S$ onde $\exp_p$ é un difeomorfismo. Tomamos $R>0$ tal que $B(\mathbf{0},R)\subset U$. Entón $\exp_p\colon B(\mathbf{0},R)\to B_R(p)$ segue sendo un difeomorfismo. Sexa $\{e_1,e_2\}$ unha base ortonormal de $T_p S$.
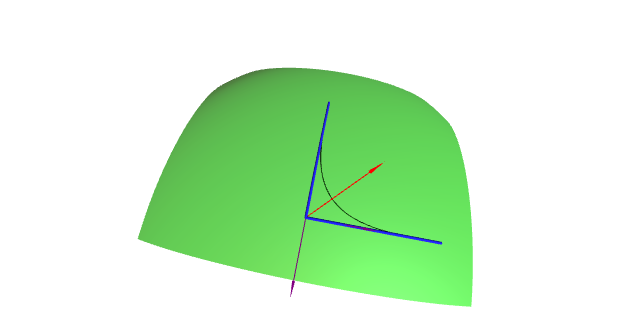
Definímo-la aplicación \[ \tilde{\mathbf{x}}(r,\theta) =\exp_p\bigl(r(\cos\theta) e_1 + r(\sin\theta) e_2\bigr). \] Esta definición ten sentido polo menos en $(-R,R)\times\R$.

Se restriximos $\tilde{\mathbf{x}}$ a unha veciñanza onde as coordenadas polares sexan un difeomorfismo (por exemplo en $(0,R)\times(-\pi,\pi)$), entón a restricción $\mathbf{x}$ de $\tilde{\mathbf{x}}$ a ese aberto define unha parametrización de $S$. Estas chámanse coordenadas polares xeodésicas.

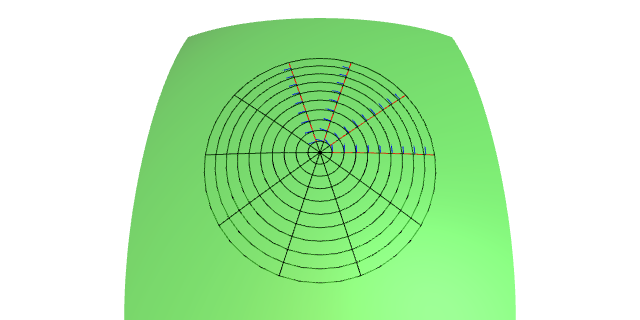
Fixémonos en que as curvas $r$-paramétricas de $\tilde{\mathbf{x}}$ son as xeodésicas radiais, mentres que as curvas $\theta$-paramétricas, son parametrizacións das circunferencias xeodésicas.
As xeodésicas radiais en $p$ son ortogonais ás circunferencias xeodésicas $S_r(p)$.
Temos que probar $\langle\frac{\partial\tilde{\mathbf{x}}}{\partial r}, \frac{\partial\tilde{\mathbf{x}}}{\partial \theta}\rangle=0$ para todo $(r,\theta)$.
En primeiro lugar, como a norma da velocidade das xeodésicas é constante, \[ \begin{aligned} \langle\frac{\partial\tilde{\mathbf{x}}}{\partial r}, \frac{\partial\tilde{\mathbf{x}}}{\partial r}\rangle &{}=\lVert\gamma_{(\cos\theta)e_1+(\sin\theta)e_2}'(r)\rVert^2\\ &{}=\lVert(\cos\theta)e_1+(\sin\theta)e_2\rVert^2=1. \end{aligned} \]
Agora ben, como a compoñente tanxente da aceleración dunha xeodésica é nula, a fórmula de Leibnitz para a derivada dun producto escalar implica \[ \begin{aligned} \frac{\partial}{\partial r}\langle\frac{\partial\tilde{\mathbf{x}}}{\partial r}, \frac{\partial\tilde{\mathbf{x}}}{\partial \theta}\rangle &{}=\langle\frac{\partial^2\tilde{\mathbf{x}}}{\partial r^2}, \frac{\partial\tilde{\mathbf{x}}}{\partial \theta}\rangle +\langle\frac{\partial\tilde{\mathbf{x}}}{\partial r}, \frac{\partial^2\tilde{\mathbf{x}}}{\partial r\partial\theta}\rangle\\ &{}=\frac{1}{2}\frac{\partial}{\partial\theta} \langle\frac{\partial\tilde{\mathbf{x}}}{\partial r}, \frac{\partial\tilde{\mathbf{x}}}{\partial r}\rangle=0. \end{aligned} \]
Por outro lado, para calquera $\theta$ temos $\tilde{\mathbf{x}}(0,\theta)=p$, co que $\frac{\partial\tilde{\mathbf{x}}}{\partial \theta}(0,\theta)=0$. Isto implica, \[ \langle \frac{\partial\tilde{\mathbf{x}}}{\partial r}(0,\theta), \frac{\partial\tilde{\mathbf{x}}}{\partial \theta}(0,\theta)\rangle = 0. \] Por tanto a función \[ r\mapsto \langle \frac{\partial\tilde{\mathbf{x}}}{\partial r}(r,\theta), \frac{\partial\tilde{\mathbf{x}}}{\partial \theta}(r,\theta)\rangle \] é constantemente igual a cero, que é o que queriamos probar.
Para as coordenadas polares xeodésicas $\mathbf{x}(r,\theta)$ temos \[ \begin{aligned} g_{rr} &{}=1, & g_{r\theta}=0. \end{aligned} \]
Defínese o campo de vectores radial en $p$ como \[ \xi_{\tilde{\mathbf{x}}(r,\theta)} =\frac{\partial \tilde{\mathbf{x}}}{\partial r}(r,\theta), \] para cada $q\in B_R(p)\setminus\{p\}$. Fixémonos que pola periodicidade en $\theta$ a definición é correcta.
É habitual denota-lo campo de vectores radial por $\frac{\partial}{\partial r}$. Non obstante preferimos non facelo aquí para evitar confusión coa notación das derivadas parciais.
Se nos restrinximos a un aberto onte $\tilde{\mathbf{x}}$ é unha parametrización $\mathbf{x}$ entón témo-la relación \[ \xi_{\mathbf{x}(r,\theta)} =\mathbf{x}_r(r,\theta). \] En consecuencia, o campo de vectores radial coincide en cada punto co vector tanxente á correspondente xeodésica radial nese punto. En particular, o fluxo do campo radial son as xeodésicas radiais.

Tamén definímo-la función distancia radial en $p$, $\mathsf{r}\colon B_R(p)\to\R$, como \[ \mathsf{r}(\mathbf{x}(r,\theta))=r. \]
Como consecuencia do lema de Gauss obtemos $\langle\xi,\xi\rangle=1$. Máis aínda,
$\grad\,\mathsf{r}=\xi$.
Sexa $q=\mathbf{x}(r_0,\theta_0)\in B_R(p)$ e $v\in T_q S$. Podemos escribir en coordenadas $v=a\mathbf{x}_r(r_0,\theta_0)+b\mathbf{x}_r(r_0,\theta_0)$. Entón, \[ \begin{aligned} \langle(\grad\,\mathsf{r})_q,v\rangle &{}=\textup{d}\mathsf{r}_q(v)\\[1ex] &{}=\textup{d}\mathsf{r}_{\mathbf{x}(r_0,\theta_0)} (a\mathbf{x}_r(r_0,\theta_0)+b\mathbf{x}_r(r_0,\theta_0))\\ &{}=\frac{d}{dt}\Big\vert_0 \mathsf{r} \bigl(\mathbf{x}(r_0+at,\theta_0+bt)\bigr)\\ &{}=\frac{d}{dt}\Big\vert_0 (r_0+at)=a\\[1ex] &{}=\langle\mathbf{x}_r(r_0,\theta_0), a\mathbf{x}_r(r_0,\theta_0)+b\mathbf{x}_r(r_0,\theta_0)\rangle\\[2ex] &{}=\langle\xi_q,v\rangle, \end{aligned} \] e como $q$ e $v$ son arbitrarios, dedúcese o resultado.
Distancia riemanniana
Sexa $S$ unha superficie regular.
Unha aplicación continua $\gamma\colon[a,b]\to S$ chámase un segmento de curva regular a cachos, ou abreviadamente, unha curva admisible, se existe unha partición $a=t_0<t_1<\dots<t_k=b$ de xeito que $\gamma_{\vert [t_i,t_{i+1}]}$ é unha curva regular (é dicir, diferenciable con derivada non nula) para cada $i=1,\dots,k$.
Para unha curva admisible denótanse as derivadas laterais nos puntos da partición como \[ \begin{aligned} \gamma'(t_i^-) &{}=\lim_{t\to t_i^-}\gamma'(t),\\ \gamma'(t_i^+) &{}=\lim_{t\to t_i^+}\gamma'(t). \end{aligned} \] Os puntos $\gamma(t_i)$ chámanse os vértices da curva.
A lonxitude dunha curva admisible $\gamma$ como a anterior defínese como \[ L(\gamma)=\sum_{i=1}^k L(\gamma_{\vert[t_i,t_{i+1}]}). \]
Toda curva admisible pode ser parametrizada por lonxitude de arco $s$, é dicir, $\lVert\gamma'(s)\rVert=1$ para todo $s$. O procedemento é análogo que para curvas diferenciables, simplemente tendo en conta que a integral se fai a cachos: \[ s(t)=L(\gamma_{\vert[a,t]})=\int_a^t\lVert\gamma'(u)\rVert\,\textup{d}u. \] É sinxelo ver, empregando o teorema de cambio de variable, que a lonxitude dunha curva admisible non depende da parametrización.
O concepto de campo de vectores tanxente ó longo dunha curva admisible é análogo a cando a curva é diferenciable.
Sexa $S$ unha superficie regular, $p\in S$, e $R>0$ onde $\exp_p\colon B(0,R)\to B_R(p)$ é un difeomorfismo. Se $\gamma$ é a xeodésica radial que une $p$ con $q\in B_R(p)$, entón $L(\gamma)\leq L(\alpha)$ para calquera curva admisible $\alpha$ que une $p$ con $q$.
Coas notacións anteriores sexa $q\in B_R(p)$; logo, podemos poñer $q=\exp_p(v)$ con $\lVert v\rVert=\epsilon < R$.
Tomámo-la xeodésica radial $\gamma(t)=\exp_p(tv)$, que satisfai \[ \begin{aligned} L(\gamma) &{}=\int_0^1\lVert\gamma'\rVert=\int_0^1\lVert v\rVert\\[1ex] &{}=\lVert v\rVert=\epsilon. \end{aligned} \]
Sexa agora $\alpha\colon[0,1]\to S$ unha curva admisible con $\alpha(0)=p$ e $\alpha(1)=q$. Temos que ver que $L(\alpha)\geq\epsilon$.
Definimos \[ \begin{aligned} a &{}=\sup_{[0,1]} \alpha^{-1}(\{p\}) = \max_{[0,1]}\alpha^{-1}(\{p\}),\\ b &{}=\inf_{[a,1]} \alpha^{-1}(S_\epsilon(p)) = \min_{[a,1]}\alpha^{-1}(S_\epsilon(p)). \end{aligned} \] Nótese que ámbalas dúas definicións son correctas pola compacidade de $[0,1]$.
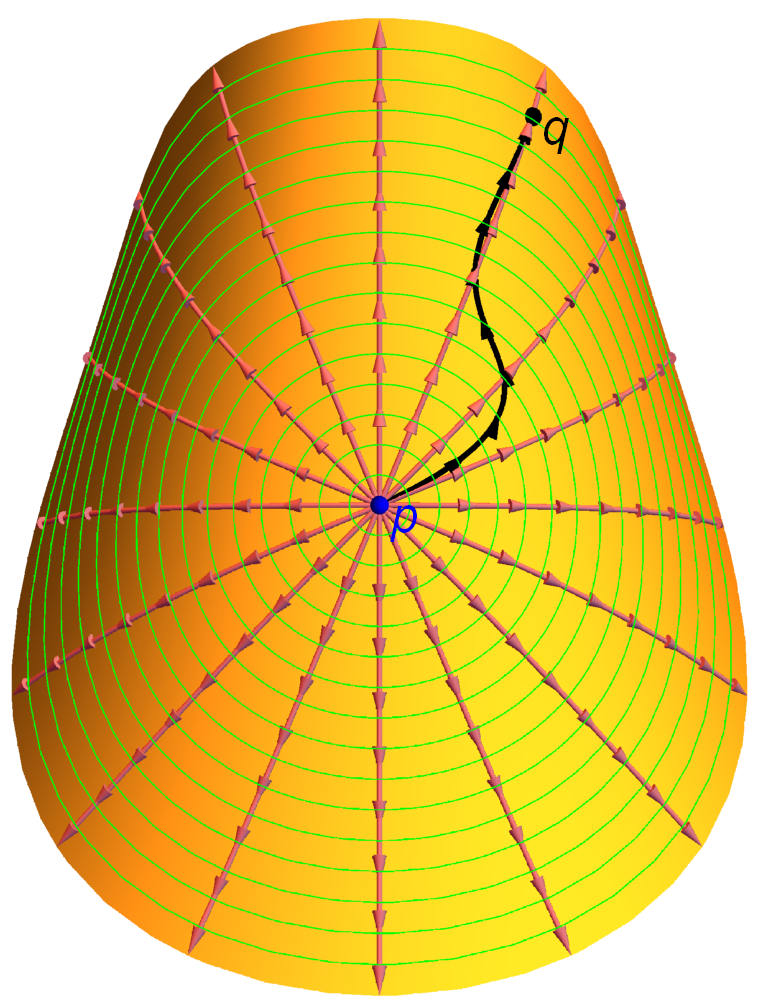
Temos que $\alpha((a,b))\subset B_\epsilon(p)$, onde o campo de vectores radial $\xi$ está definido. Para ver isto, sexa $\epsilon<s<R$, e definímo-la función $\tilde{\mathsf{r}}\colon S\to\R$ como \[ \tilde{\mathsf{r}}(x)= \begin{cases} \mathsf{r}(x) & x\in\overline{B_s(p)},\\[1ex] s & x\in S\setminus B_s(p). \end{cases} \] Esta función é continua por ser combinada de dúas continuas. Se existise $t_0\in(a,b)$ tal que $\alpha(t_0)\not\in B_\epsilon(p)$ teriamos $\tilde{\mathsf{r}}(\alpha(t_0))=s$. Polo teorema de Bolzano ten que existir $c\in[a,t_0]$ tal que $\tilde{\mathsf{r}}(\alpha(c))=\epsilon$, o que contradí a definición de $b$.
Empregando a desigualdade de Cauchy-Schwartz, tendo en conta que $\lVert\xi\rVert=1$, e o lema de Gauss, \[ \begin{aligned} L(\alpha) &{}=\int_0^1\lVert\alpha'\rVert \geq \int_a^b\lVert\alpha'(t)\rVert\,\textup{d}t\\ &{}\geq \int_a^b \Bigl\langle\alpha'(t), \xi_{\alpha(t)}\Bigr\rangle\,\textup{d}t\\ &{}=\int_a^b \langle\alpha'(t),(\grad\,\mathsf{r})_{\alpha(t)}\,\textup{d}t\\ &{}=\int_a^b \textup{d}\mathsf{r}_{\alpha(t)}(\alpha'(t))\,\textup{d}t\\ &{}=\int_a^b\frac{d}{dt}\mathsf{r}(\alpha(t))\,\textup{d}t\\ &{}=\mathsf{r}(\alpha(b))-\mathsf{r}(\alpha(a))=\epsilon, \end{aligned} \] como queriamos ver. (Nótese que nas integrais de arriba non consideramos, por comodidade, os puntos de non diferenciabilidade de $\alpha$.)
Unha curva admisible $\gamma\colon[a,b]\to S$ tal que $\gamma(a)=p$ e $\gamma(b)=q$ dise minimizante se $L(\gamma)\leq L(\alpha)$ para calquera curva admisible $\alpha\colon[c,d]\to S$ tal que $\alpha(c)=p$ e $\alpha(d)=q$.
O resultado anterior di que toda xeodésica é localmente minimizante.
Toda curva minimizante parametrizada por lonxitude de arco é unha xeodésica.
Sexa $\gamma\colon[a,b]\to S$ unha curva minimizante tal que $\gamma(a)=p$ e $\gamma(b)=q$, parametrizada por lonxitude de arco a trozos na partición $a=a_0<a_1<\dots<a_k=b$.
En primeiro lugar vexamos que $\gamma_{\vert[a_{i-1},a_{i}]}$ é unha xeodésica.
Sexa $\varphi\colon[a,b]\to\R$ unha función diferenciable tal que $\varphi_{\vert(a_{i-1},a_{i})}>0$ e $\varphi_{\vert[a,b]\setminus(a_{i-1},a_{i})}=0$. Consideramos \[ \Gamma(s,t)=\exp_{\gamma(t)}\Bigl(s\,\varphi(t)\frac{D\gamma'}{dt}(t)\Bigr), \] que é diferenciable.
Temos que \[ \begin{aligned} \Gamma(s,a) &{}=p,\\[1ex] \Gamma(s,b) &{}=q, \end{aligned} \] e por tanto, para cada $s$, $t\mapsto\Gamma_s(t)=\Gamma(s,t)$ é unha curva unindo $p$ con $q$. Ademais, \[ \Gamma_0(t)=\Gamma(0,t)=\exp_{\gamma(t)}(0)=\gamma(t). \]
Como $\gamma=\Gamma_0$ é minimizante, é un mínimo da función $s\mapsto L(\Gamma_s)$. Por tanto, \[ \begin{aligned} 0 &{}=\frac{d}{ds}\bigg\vert_0 L(\Gamma_s)\\ &{}=\frac{d}{ds}\bigg\vert_0 \sum_{j=1}^k \int_{a_{j-1}}^{a_j}\lVert\Gamma_s'(t)\rVert\,\textup{d}t\\ &{}=\frac{d}{ds}\bigg\vert_0 \sum_{j=1}^k \int_{a_{j-1}}^{a_j}\sqrt{ \langle\frac{\partial \Gamma}{\partial t}(s,t), \frac{\partial \Gamma}{\partial t}(s,t)\rangle }\,\textup{d}t\\ &{}=\sum_{j=1}^k\biggl( \Bigl\langle\frac{\partial\Gamma}{\partial s}(0,a_j), \frac{\partial\Gamma}{\partial t}(0,a_j^-)\Bigr\rangle -\Bigl\langle\frac{\partial\Gamma}{\partial s}(0,a_{j-1}), \frac{\partial\Gamma}{\partial t}(0,a_{j-1}^+)\Bigr\rangle \biggr)\\ &\phantom{{}={}}-\sum_{j=1}^k\int_{a_{j-1}}^{a_j} \Bigl\langle\frac{\partial\Gamma}{\partial s}(0,t), \frac{D\gamma'}{dt}(t)\Bigr\rangle\,\textup{d}t\\ &{}=-\int_{a_i}^{a_{i+1}}\varphi(t) \Bigl\lVert\frac{D\gamma'}{dt}(t)\Bigr\rVert\,\textup{d}t. \end{aligned} \] Isto implica $\frac{D\gamma'}{dt}=0$, e por tanto, $\gamma_{\vert[a_i,a_{i+1}]}$ é unha xeodésica.
Vexamos agora que $\gamma$ non ten esquinas.
Fixado $i\in\{1,\dots,k-1\}$ vexamos que $\gamma'(a_i^-)=\gamma'(a_i^+)$. De non ser así, tomemos $V$ un campo de vectores ó longo de $\gamma$ tal que $V(a_i)=\gamma'(a_i^+)-\gamma'(a_i^-)$, e $V(a_j)=0$ se $j\neq i$. Consideramos \[ \Gamma(s,t)=\exp_{\gamma(t)}\bigl(s\, V(t)\bigr), \] que tamén é diferenciable.
Igual ca no caso anterior \[ \begin{aligned} \Gamma(s,a) &{}=p,\\[1ex] \Gamma(s,b) &{}=q,\\[1ex] \Gamma(0,t) &{}=\exp_{\gamma(t)}(0)=\gamma(t). \end{aligned} \] Como $\gamma=\Gamma_0$ é un mínimo de $L(\Gamma_s)$, temos \[ \begin{aligned} 0 &{}=\frac{d}{ds}\bigg\vert_0 L(\Gamma_s)\\ &{}=\sum_{j=1}^k\biggl( \Bigl\langle\frac{\partial\Gamma}{\partial s}(0,a_j), \frac{\partial\Gamma}{\partial t}(0,a_j^-)\Bigr\rangle -\Bigl\langle\frac{\partial\Gamma}{\partial s}(0,a_{j-1}), \frac{\partial\Gamma}{\partial t}(0,a_{j-1}^+)\Bigr\rangle \biggr)\\ &\phantom{{}={}}-\sum_{j=1}^k\int_{a_{j-1}}^{a_j} \Bigl\langle\frac{\partial\Gamma}{\partial s}(0,t), \frac{D\gamma'}{dt}(t)\Bigr\rangle\,\textup{d}t\\ &{}=-\lVert\gamma'(a_i^+)-\gamma'(a_i^-)\rVert^2. \end{aligned} \] En consecuencia, $\gamma'(a_i^-)=\gamma'(a_i^+)$.
Nótese finalmente que como $\gamma'(a_i^-)=\gamma'(a_i^+)$ para cada $i$, se segue, por unicidade das xeodésicas que $\gamma_{\vert[a_i,a_{i+1}]}$ é a continuación da xeodésica $\gamma_{\vert[a_{i-1},a_i]}$, e por tanto, $\gamma$ é diferenciable $C^\infty$.
No transcurso da demostración do resultado anterior vimos unha fórmula que extraemos no seguinte resultado, despois de refinar un pouco a notación:
Sexa $S$ unha superficie e $\gamma\colon[a,b]\to S$ unha curva admisible parametrizada por arco a trozos na partición $a=a_0<a_1<\dots<a_k=b$. Sexa $\Gamma\colon(-\epsilon,\epsilon)\times[a,b]\to S$ unha aplicación continua, diferenciable en cada $(-\epsilon,\epsilon)\times[a_{i-1},a_i]$, tal que $\Gamma_s(t)=\Gamma(s,t)$ é unha curva admisible para cada $s\in(-\epsilon,\epsilon)$, e de xeito que $\Gamma_0=\gamma$. Entón, se denotamos $V(t)=\frac{\partial\Gamma}{\partial s}(0,t)$, temos \[ \begin{aligned} \frac{d}{ds}\bigg\vert_0 L(\Gamma_s)={} &{}-\sum_{j=1}^k\int_{a_{j-1}}^{a_j} \Bigl\langle V(t),\frac{D\gamma'}{dt}(t)\Bigr\rangle\,\textup{d}t\\ &{}-\sum_{j=1}^{k-1} \langle V(a_j),\gamma'(a_j^+)-\gamma'(a_j^-)\rangle\\[2ex] &{}+\langle V(b),\gamma'(b)\rangle -\langle V(a),\gamma'(a)\rangle. \end{aligned} \]
Supoñamos que a superficie regular $S$ é conexa.
Definímo-la función $d\colon S\times S\to\R$ como \[ d(p,q)=\inf\{L(\alpha):\text{$\alpha$ é curva admisible unindo $p$ con $q$}\}. \]
O obxectivo do que segue é ver que a función $d$ é unha distancia.
A concatenación de curvas admisibles é unha curva admisible.
Sexan $\alpha\colon[a,b]\to S$ e $\beta\colon[c,d]\to S$ dúas curvas admisibles tales que $\alpha(b)=\beta(c)$, con particións asociadas $a=x_0<x_1<\dots<x_k=b$ e $c=y_0<y_1<\dots<y_\ell=d$.
A concatenación de $\alpha$ e $\beta$ é a curva $\alpha*\beta\colon[a,b+d-c]\to S$, definida como \[ (\alpha*\beta)(t)= \begin{cases} \alpha(t) & a\leq t\leq b,\\[1ex] \beta(t-b+c) & b\leq t\leq b+d-c, \end{cases} \] que é admisible con partición \[ \begin{aligned} a&{}=x_0<x_1<\dots<x_k=b\\ &{}=y_0+b-c<y_1+b-c<\dots\\ &{}<y_\ell+b-c=d+b-c. \end{aligned} \] Despois disto, a comprobación das condicións da definición de curva admisible son inmediatas.
Todo par de puntos dunha superficie conexa poden ser unidos mediante unha curva admisible.
Sexa $S$ unha superficie e $p\in S$ un punto fixado. Definimos $A$ como o conxunto de puntos $q\in S$ tales que existe unha curva admisible unindo $p$ con $q$. É suficiente con ver que $A=S$.
Obviamente, $p\in A$, co que $A\neq\emptyset$.
Vexamos que $A$ é aberto. Sexa $q\in A$. Tomemos $\mathbf{x}\colon U\subset\R^2\to S$ unha parametrización en $q$. Como $U$ é aberto, existe $r>0$ tal que $B\bigl(\mathbf{x}^{-1}(q),r\bigr)\subset U$. Entón, $q\in\mathbf{x}\bigl(B(\mathbf{x}^{-1}(q),r)\bigr)\subset A$. En efecto, sexa $y\in \mathbf{x}\bigl(B(\mathbf{x}^{-1}(q),r)\bigr)$. Entón existe un segmento unindo $\mathbf{x}^{-1}(y)$ con $\mathbf{x}^{-1}(q)$ (pois as bólas son convexas), así que a imaxe por $\mathbf{x}$ dese segmento está contida en $\mathbf{x}\bigl(B(\mathbf{x}^{-1}(q),r)\bigr)$. É dicir, todo punto de $\mathbf{x}\bigl(B(\mathbf{x}^{-1}(q),r)\bigr)$ pode ser unido con $\mathbf{x}^{-1}(q)$ mediante unha curva regular. Xa que $q$ pode ser unido con $p$ por unha curva admisible, concatenando esta curva admisible coa curva regular anterior dá unha curva admisible unindo $p$ con calquera punto de $\mathbf{x}\bigl(B(\mathbf{x}^{-1}(q),r)\big)$. En consecuencia, $q$ é interior a $A$, e por tanto, $A$ é aberto.
O conxunto $A$ é pechado. Equivalentemente, $S\setminus A$ é aberto. A demostración é análoga ó caso anterior, xa que todo punto $q\in S\setminus A$ ten unha veciñanza homeomorfa a unha bóla, así que ningún punto desa veciñanza se pode unir a $p$ por unha curva admisible.
Como $S$ é conexa, $A=S$ o que acaba a demostración.
A aplicación $d$ é unha distancia.
En primeiro lugar, $d$ está ben definida polo lema anterior. Verificamos agora os axiomas de distancia:
- $d(p,q)\geq 0$ é obvio pois as curvas admisibles teñen lonxitude non negativa. Se $p\neq q$ entón $d(p,q)\geq d_{\R^3}(p,q)> 0$.
- $d(p,q)=d(q,p)$ pois a lonxitude non depende da parametrización.
- $d(p,q)\leq d(p,z)+d(z,q)$ pois o conxunto das curvas admisibles que unen $p$ con $q$ contén ó conxunto das curvas admisibles que unen $p$ con $a$ pasando por $z$.
Por tanto, $d$ é unha distancia.
Chámase distancia riemanniana da superficie conexa $S$ á función $d$ definida anteriormente.
Se $S$ é un plano, entón a aplicación exponencial $\exp_p(v)=p+v$ é un difeomorfismo global, así que pola propiedade minimizante das xeodésicas, neste caso aplicada a todo o plano, a distancia está realizada polas xeodésicas, que son as rectas. Por tanto, $d(p,q)=\lVert p-q\rVert$ é a distancia euclidiana usual.
Na esfera $\mathbb{S}^2$ de radio $1$, a aplicación exponencial vén dada por \[ \exp_p(v)=\bigl(\cos\lVert v\rVert\bigr)p +\frac{1}{\lVert v\rVert}\bigl(\sin\lVert v\rVert\bigr)v. \] A restricción $\exp_p\colon B(\mathbf{0},\pi)\to\mathbb{S}^2\setminus\{-p\}$ é un difeomorfismo con inversa \[ \exp_p^{-1}(q)= \frac{\sphericalangle(p,q)}{\sin\sphericalangle(p,q)} \bigl(-\langle p,q\rangle\, p+q\bigr). \] Por tanto, se $q\neq -p$, empregando a propiedade minimizante local das xeodésicas temos \[ \begin{aligned} d(p,q) &{}=\lVert\exp_p^{-1}(q)\rVert\\ &{}=\sphericalangle(p,q)\\ &{}=\arccos\langle p,q\rangle. \end{aligned} \]
Por continuidade obtense a mesma fórmula para $q=-p$, co que $d(p,q)=\sphericalangle(p,q)=\arccos\langle p,q\rangle$ é o ángulo que forman os vectores de posición dos dous puntos.

Localmente a distancia é realizada pola lonxitude dunha xeodésica.
Sexan $p,q\in S$ con $q\in B_R(p)$ onde $\exp_p$ é un difeomorfismo. Vimos entón que a lonxitude da xeodésica radial $\gamma$ que une $p$ con $q$ minora tódalas lonxitudes de curvas unindo $p$ con $q$. Entón $d(p,q)=L(\gamma)$.
Se $r>0$ é suficientemente pequeno: \[ \begin{aligned} B_r(p) &{}=\{q\in S:d(p,q)<r\},\\[1ex] S_r(p) &{}=\{q\in S:d(p,q)=r\}. \end{aligned} \]
Simplemente se toma un $r>0$ suficientemente pequeno onde $\exp_p$ é un difeomorfismo, e úsase que a distancia riemanniana é realizada por xeodésicas radiais.
A topoloxía inducida pola distancia $d$ coincide coa topoloxía de $S$.
Como as parametrizacións son homeomorfismos, os conxuntos $B_r(p)=\exp_p(B_{T_p S}(\mathbf{0},r))$ xeran a topoloxía de $S$. Pero para $r$ suficientemente pequenos as bólas xeodésicas coinciden coas bólas para a distancia $d$.
O seguinte é un dos teoremas máis importantes da xeometría diferencial, pero neste curso non incluirémo-la súa demostración.
Sexa $S$ unha superficie regular conexa. As seguintes afirmacións son equivalentes:
- $S$ é xeodesicamente completa, é dicir, toda xeodésica está definida en todo $\R$.
- $\exp_p$ está definida en todo $T_p S$ para todo $p\in S$.
- $S$ é un espacio métrico completo coa distancia $d$.
Diremos que unha superficie conexa é completa se se satisfai calquera dos enunciados equivalentes anteriores.
Sexa $S$ unha superficie completa coa distancia riemanniana $d$. Entón todo para de puntos de $S$ poden ser unidos por unha xeodésica minimizante.
Unha bóla aberta nun plano non é completa, pero calquera par de puntos desa bóla poden ser unidos por unha xeodésica minimizante.
Aplicacións das coordenadas polares xeodésicas
Sexa $R>0$ tal que $\exp_p\colon B(\mathbf{0},R)\to B_R(p)\subset S$ é un difeomorfismo. Sexa $\{e_1,e_2\}$ base ortonormal de $T_p S$ e considerémo-las coordenadas normais $\mathbf{y}(u_1,u_2)=\exp_p(u_1 e_1+u_2 e_2)$. Tamén temos \[ \begin{aligned} \tilde{\mathbf{x}}(r,\theta) &{}=\mathbf{y}(r \cos\theta, r \sin\theta)\\ &{}=\exp_p(r(\cos\theta) e_1+r(\sin\theta) e_2). \end{aligned} \] Nun aberto onde esta aplicación é un difeomorfismo, denotemos por $\mathbf{x}$ ás correspondentes coordenadas polares xeodésicas.
Calculámo-la curvatura de Gauss en coordenadas polares xeodésicas. Como non temos información sobre a superficie, temos que calcula-la empregando as fórmulas do teorema egregium para os símbolos de Chirstoffel e a curvatura: \[ \begin{aligned} \Gamma_{ij}^k &{}=\frac{1}{2}\sum_l g^{kl}\left( \frac{\partial g_{jl}}{\partial u_i} +\frac{\partial g_{il}}{\partial u_j} -\frac{\partial g_{ij}}{\partial u_l}\right),\\ K &{}=\frac{1}{g_{11}}\left( \frac{\partial \Gamma_{11}^2}{\partial u_2} -\frac{\partial \Gamma_{12}^2}{\partial u_1} +\Gamma_{11}^1\Gamma_{12}^2 +\Gamma_{11}^2\Gamma_{22}^2 -\Gamma_{12}^1\Gamma_{11}^2 -(\Gamma_{12}^2)^2 \right). \end{aligned} \]
Obtemos: \[ \begin{aligned} \Gamma_{11}^1 & {}=0,\\[2ex] \Gamma_{11}^2 & {}=0,\\[2ex] \Gamma_{12}^1 & {}=\Gamma_{21}^1=0,\\[1ex] \Gamma_{12}^2 &{}=\Gamma_{21}^2=\frac{1}{2 g_{\theta\theta}} \frac{\partial g_{\theta\theta}}{\partial r},\\ \Gamma_{22}^1 &{}=-\frac{1}{2}\frac{\partial g_{\theta\theta}}{\partial r},\\ \Gamma_{22}^2 & {}=-\frac{1}{2 g_{\theta\theta}} \frac{\partial g_{\theta\theta}}{\partial\theta}. \end{aligned} \]
Substituíndo na ecuación de Gauss: \[ \begin{aligned} K &{}=\frac{1}{2 g_{\theta\theta}}\left( \frac{1}{2 g_{\theta\theta}} \left(\frac{\partial g_{\theta\theta}}{\partial r}\right)^2 -\frac{\partial^2 g_{\theta\theta}}{\partial r^2} \right)\\ &{}=-\frac{1}{\sqrt{g_{\theta\theta}}} \frac{\partial^2}{\partial r^2}\sqrt{g_{\theta\theta}}. \end{aligned} \]
Como $\tilde{\mathbf{x}}(0,\theta)=p$ para todo $\theta$, temos \[ \lim_{r\to 0}\sqrt{g_{\theta\theta}(r,\theta)} =\sqrt{\Bigl\langle\frac{\partial\tilde{\mathbf{x}}}{\partial\theta}(0,\theta), \frac{\partial\tilde{\mathbf{x}}}{\partial\theta}(0,\theta)\Bigr\rangle} =0. \]
Para o cálculo de $\lim_{r\to 0}\frac{\partial}{\partial r}\sqrt{g_{\theta\theta}(r,\theta)}$ aplicámo-la regra da cadea primeiro pasando polas coordenadas normais \[ \begin{aligned} \frac{\partial{\tilde{\mathbf{x}}}}{\partial\theta}(r,\theta) &{}=-\mathbf{y}_1(r\cos\theta,r\sin\theta)\,r\sin\theta +\mathbf{y}_2(r\cos\theta,r\sin\theta)\,r \cos\theta. \end{aligned} \] Definimos \[ \begin{aligned} H(r,\theta)= &{}\,g_{11}(r\cos\theta,r\sin\theta)\,\sin^2\theta\\ &{}+2 g_{12}(r\cos\theta,r\sin\theta)\,\sin\theta\cos\theta\\ &{}+g_{22}(r\cos\theta,r\sin\theta)\,\cos^2\theta. \end{aligned} \] Esta é unha función diferenciable tal que $H(0,\theta)=1$. Ademais, \[ \begin{aligned} \lim_{r\to 0}\frac{\partial}{\partial r}\sqrt{g_{\theta\theta}(r,\theta)} &{}=\lim_{r\to 0}\frac{\partial}{\partial r} \sqrt{\Bigl\langle\frac{\partial\tilde{\mathbf{x}}}{\partial\theta}(r,\theta), \frac{\partial\tilde{\mathbf{x}}}{\partial\theta}(r,\theta)\Bigr\rangle}\\ &{}=\lim_{r\to 0}\frac{\partial}{\partial r} \Bigl(r\sqrt{H(r,\theta)}\Bigr)\\ &{}=\lim_{r\to 0} \biggl(\sqrt{H(r,\theta)} +r\frac{\frac{\partial H}{\partial r}(r,\theta)}{2\sqrt{H(r,\theta)}}\biggr) =1. \end{aligned} \]
Por tanto, se denotamos $F=\sqrt{g_{\theta\theta}}$ témo-la EDO: \[ \begin{aligned} &{} \frac{\partial^2 F}{\partial r^2}(r,\theta)+K(\mathbf{x}(r,\theta)) F(r,\theta) =0,\\[1ex] &{}F(0,\theta) =0,\\ &{}\frac{\partial F}{\partial r}(0,\theta) =1, \end{aligned} \] para cada valor de $\theta$.
Dúas superficies coa mesma curvatura de Gauss constante son localmente isométricas.
Sexan $S$ e $\bar{S}$ dúas superficies coa mesma curvatura de Gauss constante $K$. Suporemos por exemplo $K<0$, sendo os outros casos análogos.
Sexa $p\in S$ e $\{e_1,e_2\}$ base ortonormal de $T_p S$. Tomamos en $p$ coordenadas polares xeodésicas $\mathbf{x}$ con respecto da base $\{e_1,e_2\}$. Analogamente, sexa $\bar{p}\in \bar{S}$ e $\{\bar{e}_1,\bar{e}_2\}$ base ortonormal de $T_{\bar{p}} \bar{S}$. Tomamos en $\bar{p}$ coordenadas polares xeodésicas $\bar{\mathbf{x}}$ con respecto da base $\{\bar{e}_1,\bar{e}_2\}$. Asumímo-las notación en $S$ e $\bar{S}$ que sexan coherentes coas anteriores.
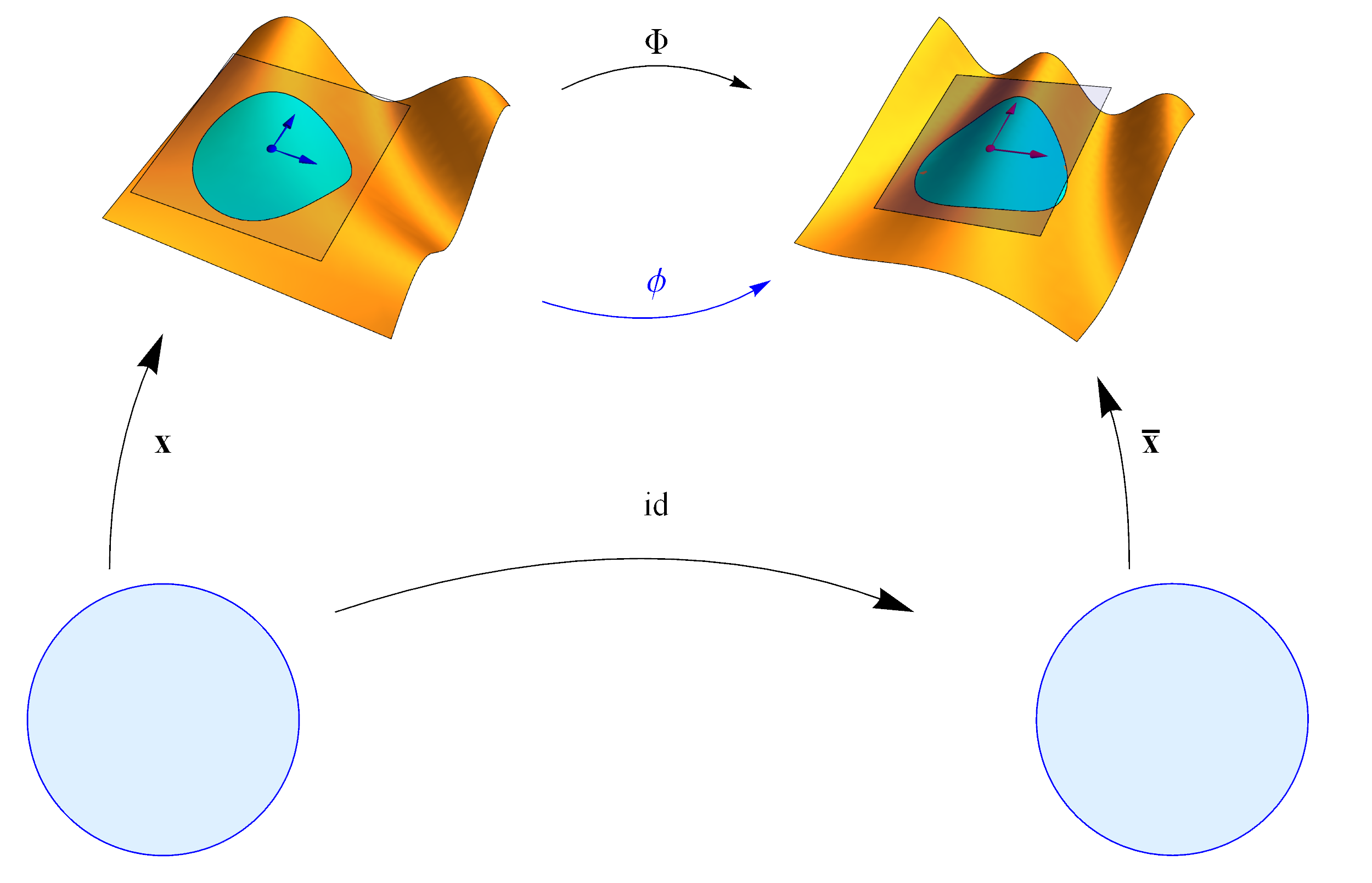
Sexa $\phi\colon T_p S\to T_{\bar{p}} \bar{S}$ a isometría linear tal que $\phi(e_i)=\bar{e}_i$, $i=1,2$. Definimos $\Phi=\bar{\exp}_{\bar{p}}\circ\phi\circ\exp_p$. Entón, $\Phi(\mathbf{x}(r,\theta))=\bar{\mathbf{x}}(r,\theta)$, é dicir, que en coordenadas polares xeodésicas a aplicación $\Phi$ é a identidade.
Resolvendo a anterior ecuación diferencial obtemos $F(r,\theta)=\frac{1}{\sqrt{-K}}\sinh r\sqrt{-K}$ para as dúas superficies. Combinando isto co lema de Gauss temos $g_{rr}=1=\bar{g}_{11}$, $g_{r\theta}=0=\bar{g}_{r\theta}$ e $g_{\theta\theta}=F^2=\bar{g}_{\theta\theta}$, o que implica que $\Phi$ é unha isometría.
A curvatura positiva achega as xeodésicas.
O seguinte gráfico amosa dúas xeodésicas que empezan nunha zona con curvatura positiva no toro. A curvatura positiva fai que esas súas xeodésicas estean sempre preto unha da outra.
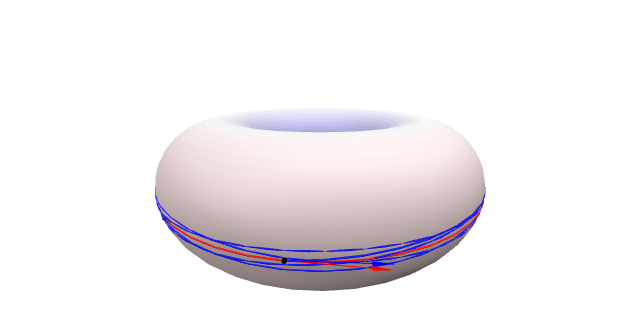
A curvatura negativa afasta as xeodésicas.
O seguinte gráfico amosa dúas xeodésicas que comenzan nunha zona de curvatura negativa do toro. Vemos que en relativamente pouco tempo se afastan e as súas trazas axiña non teñen nada que ver.
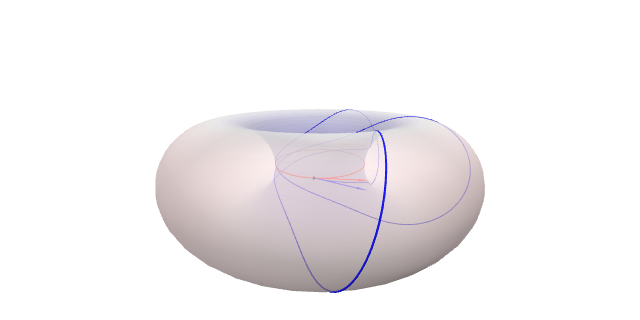
Xustificarémo-la segunda destas afirmacións, sendo a primeira similar. Supoñamos que a superficie $S$ ten curvatura de Gauss negativa arredor dun punto $p$. Tomamos coordenadas polares xeodésicas $\mathbf{x}$ arredor de $p$. Sexan $\gamma_1(t)=\mathbf{x}(t,\theta_1)$ e $\gamma_2(t)=\mathbf{x}(t,\theta_2)$ dúas xeodésicas radiais. Para $r$ fixado sexa $\alpha(\theta)=\mathbf{x}(r,\theta)$, $\theta\in[\theta_1,\theta_2]$. Unha medida de como se afasta $\gamma_1$ de $\gamma_2$ é a lonxitude $L(\alpha)$ de $\alpha$.
Denotando $F(r,\theta)=\sqrt{g_{\theta\theta}(r,\theta)}$, temos $F(0,\theta)=0$, $\frac{\partial F}{\partial r}(0,\theta)=1$, e $\frac{\partial^2 F}{\partial r^2}=-K F> 0$. Por tanto, empregando o lema de Gauss temos \[ \begin{aligned} L(\alpha) &{}=\int_{\theta_1}^{\theta_2} \lVert\alpha'(\theta)\rVert\,\textup{d}\theta\\ &{}=\int_{\theta_1}^{\theta_2} \sqrt{g_{\theta\theta}(r,\theta)}\,\textup{d}\theta\\[1ex] &{}\geq\int_{\theta_1}^{\theta_2} r\,\textup{d}\theta\\[1ex] &{}= r(\theta_2-\theta_1), \end{aligned} \] o cal quere dicir que as xeodésicas (para $r$ pequeno) se afastarían máis do que o farían dúas xeodésicas radiais no plano.
O seguinte gráfico é unha xeodésica calculada numericamente. Dita xeodésica debería corresponderse co círculo interior do toro, pero os erros de redondeo fan que as pequenas desviacións da xeodésica teórica se propaguen exponencialmente ata o punto de que non podemos fiarnos do resultado numérico obtido.

Sexa $f\colon I\subset\R\to\R$ unha función diferenciable tal que $f(0)=0$, $f'(0)=1$ e $f''(0)>0$. Probar que existe $\epsilon>0$ tal que $f(x)> x$ se $0<x<\epsilon$.
As seguintes figuras permiten calcular numericamente as xeodésicas do toro partindo de dous puntos dados.

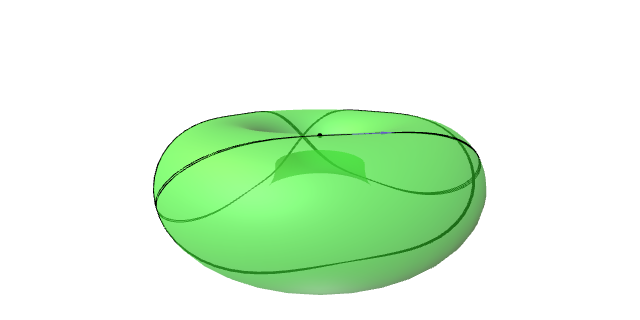
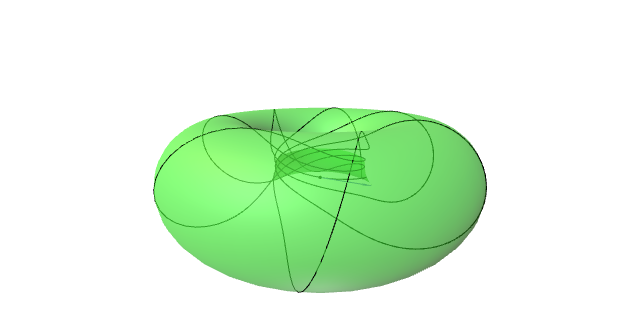
Se $S$ é unha superficie regular, a súa curvatura de Gauss satisfai: \[ K(p)=\lim_{r\to 0}\frac{3}{\pi}\frac{2\pi r-L(S_r(p))}{r^3}. \]
Calculámo-la lonxitude dunha pequena circunferencia xeodésica de radio $r$ arredor dun punto $p\in S$, $\alpha(\theta)=\mathbf{x}(t,\theta)$ escrita en coordenadas polares xeodésicas.
Recordando que $F=\sqrt{g_{\theta\theta}}$ satisfai a ecuación diferencial $\frac{\partial^2 F}{\partial r^2}+KF=0$ obtemos \[ \begin{aligned} F(0,\theta) &{}= 0,\\[1ex] \frac{\partial F}{\partial r}(0,\theta) &{}= 1,\\ \frac{\partial^2 F}{\partial r^2}(0,\theta) &{}= 0,\\ \frac{\partial^3 F}{\partial r^3}(0,\theta) &{}= -K(p).\\ \end{aligned} \]
Entón temos \[ \begin{aligned} L(\alpha) &{}=\int_0^{2\pi}\lVert\alpha'(\theta)\rVert\,\textup{d}\theta\\ &{}=\int_0^{2\pi} \sqrt{g_{\theta\theta}(r,\theta)}\,\textup{d}\theta\\ &{}=\int_0^{2\pi} \Bigl(r-\frac{K(p)}{3!}r^3+O(r^4)\Bigr)\,\textup{d}\theta\\ &{}=2\pi r-\frac{2\pi K(p)}{6}r^3+O(r^4), \end{aligned} \] de onde se deduce o resultado.
O resultado anterior dá outra interpretación intrínseca da curvatura de Gauss. Como a lonxitude dunha circunferencia xeodésica só depende dos coeficientes da primeira forma fundamental, isto constitúe un novo xeito de entende-lo teorema egregium.