Exames de anos anteriores

Sexa $S$ a esfera $x^2+y^2+z^2=1$ e sexa \[ \mathbf{x}(u,v) =(\cos u \cos v,\sin u \cos v,\sin v), \] unha parametrización de $S$, $-\pi<u<\pi$, $-\pi/2<v<\pi/2$.

1. Sexa o campo de vectores de $\R^3$, $\mathbf{F}(x,y,z)=(-y,x,0)$.
   1. Defini-lo concepto de campo de vectores tanxente a unha superficie ó longo dunha curva. Probar que $\mathbf{F}$ é un campo de vectores tanxente a $S$ ó longo das curvas $z=$ constante.
   2. Defini-lo concepto de campo de vectores tanxente paralelo ó longo dunha curva contida na superficie. ¿É $\mathbf{F}$ un campo de vectores tanxente paralelo ó longo da curva $z=0$.
2. Usando o teorema de Gauss-Bonnet, calcula-la área da rexión $R\subset S$, limitada polas curvas \[ \begin{aligned} C_1 &{}=\{(x,y,z)\in S: x=0\},\\[3ex] C_2 &{}=\{(\cos t,\sin t,0)\in S: -\pi/4\leq t\leq\pi/4\},\\[1ex] C_3 &{}=\Bigl\{ \Bigl(\frac{\sqrt{2}}{2}\cos t,\frac{\sqrt{2}}{2}\sin t,\frac{\sqrt{2}}{2}\Bigr) \in S: -\pi/4\leq t\leq\pi/4\Bigr\},\\ C_4 &{}=\Bigl\{ \Bigl(\frac{\sqrt{2}}{2}\cos t,\frac{\sqrt{2}}{2}\cos t,\sin t\Bigr)\in S: 0\leq t\leq\pi/4\Bigr\},\\ C_5 &{}=\Bigl\{ \Bigl(\frac{\sqrt{2}}{2}\cos t,-\frac{\sqrt{2}}{2}\cos t,\sin t\Bigr)\in S: 0\leq t\leq\pi/4\Bigr\}. \end{aligned} \]
3. Sexa $p=(1,0,0)$ e $\mathbf{w}=(0,1,1)\in T_p S$. Calcula-lo vector transportado paralelo en $S$ ó longo da curva $z=0$ do vector $\mathbf{w}$ dende o punto $p$ ata o punto $q=(\sqrt{2}/2,\sqrt{2}/2,0)$.
4. Calcula-las coordenadas en $\R^3$ do punto $\exp_p(\mathbf{v})$ de $S$ para $p=(1,0,0)\in S$ e $\mathbf{v}=(0,-\pi/4,0)\in T_p S$.

Razoar se son verdadeiras ou falsas as seguintes afirmacións:

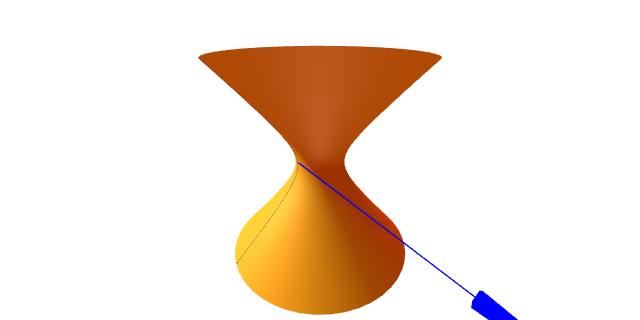
1. O cono $S=\{(x,y,z)\in\R^3:z^2=3(x^2+y^2),z>0\}$ é unha superficie orientable.
2. Sexa $S\subset\R^3$ unha superficie regular e $\pi\subset\R^3$ un plano tal que $\pi\cap S$ é unha curva regular e $\pi$ contén os vectores normais a $S$ en cada punto da curva $\pi\cap S$. Entón $\pi\cap S$ é, cando está parametrizada proporcionalmente ó arco, unha xeodésica de $S$.
3. Se a curvatura integral do elipsoide $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ vale $4\pi$, entón $a=b=c$, é dicir, o elipsoide é unha esfera.

Sexa ${V}$ un campo de vectores diferenciable, unitario, e tanxente ó longo dunha curva regular $\alpha\colon I\to S$ contida nunha superficie regular $S$ orientada por $\mathbf{N}$.

1. Demostrar que existe unha función diferenciable $\lambda\colon I\to\R$ tal que \[ \frac{DV}{dt}(t)=\lambda(t)\bigl(\mathbf{N}(t)\times V(t)\bigr), \] onde $\frac{DV}{dt}$ denota a derivada covariante do campo $V$ ó longo de $\alpha$.
2. Demostrar que se $\alpha$ está parametrizada polo parámetro lonxitude de arco $s$ e $V(s)=\alpha'(s)$, entón a función $\lambda$ é precisamente a curvatura xeodésica de $\alpha$ en $S$.

Considérase o hiperboloide dunha folla $S=\{(x,y,z)\in\mathbb{R}^{3}: x^{2}+y^{2}-z^{2}=1\}$, que pode ser parametrizado como superficie de revolución mediante \[ \mathbf{x}(t, \theta)=(\cosh t \cos \theta, \cosh t \sin\theta, \sinh t), \] $t\in\R$, $-\pi<\theta<\pi$.

Sexan $p=(1,0,0)\in S$ e $\mathbf{v}=(0,\frac{5}{2}\pi,0)\in T_pS$.

1. Calcula-lo transporte paralelo de $\mathbf{v}$ ó longo da curva intersección de $S$ co plano $y=0$.
2. Calcular $\exp_p(\mathbf{v})$.

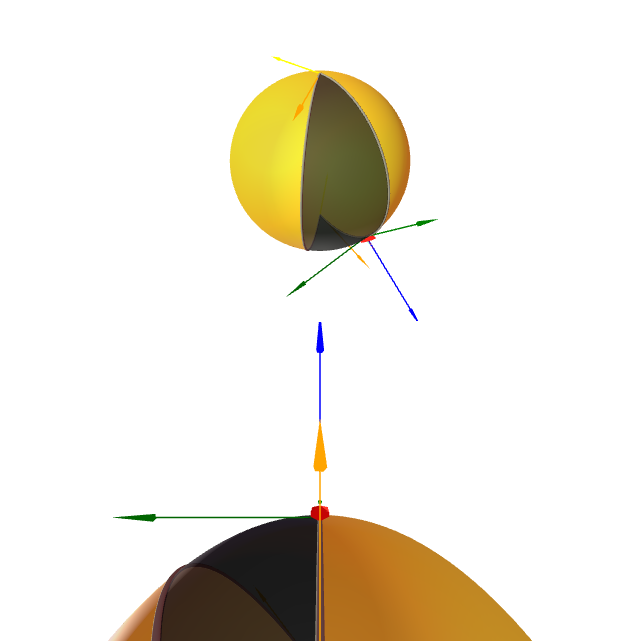
Calcula tódolos termos da fórmula de Gauss-Bonnet para a rexión da esfera $\mathbb{S}^2$ delimitada pola intersección de dita esfera cos planos $y=0$ e $y=x$, con $y\leq x$.

Responde-las seguintes cuestións xustificando a resposta:

1. ¿É orientable a superficie dada pola gráfica dunha función diferenciable?
2. ¿A curvatura integral do elipsoide $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ está dada por $4\pi \sqrt[3]{(abc)^2}$?
3. ¿Se $\exp_p(\mathbf{v})$ está definido, entón tamén o está $\exp_p(t\mathbf{v})$ para todo $t\in[0,1]$?
4. ¿As coordenadas polares xeodésicas son un sistema ortogonal de coordenadas locais?
5. ¿A curvatura xeodésica dunha curva regular é independente da súa parametrización?
6. ¿Entre dous puntos dunha superficie conexa, pode haber máis dunha xeodésica que os una?

Probar que, para cada punto $p$ dunha superficie regular $S$ e cada vector tanxente $\mathbf{v}\in T_pS$, existe unha xeodésica $\gamma\colon(-\epsilon,\epsilon)\to S$ tal que $\gamma(0)=p$ e $\gamma'(0)=\mathbf{v}$, para algún $\epsilon>0$ suficientemente pequeno. Deducir previamente as ecuacións dunha xeodésica en coordenadas locais.

Demostrar que a estructura complexa $J$ dunha superficie regular orientable $S$ en $\mathbb{R}^3$ conmuta co operador derivada covariante $\frac{D}{dt}$, é dicir, que $\frac{D}{dt}JV(t)=J\frac{D}{dt}V(t)$ para todo campo de vectores diferenciable $V(t)$ tanxente a $S$ ó longo dunha curva $\alpha(t)$ en $S$.

Considerémo-la superficie regrada $S$ parametrizada por \[ \mathbf{x}(u,v)={}(\sinh u,\,u,\,\cosh u)+v\bigl(\phi(u),\,0,\,\phi(u)\bigr), \] con $u$, $v\in\mathbb{R}$, e onde $\phi\colon\R\to\R$ é a función analítica \[ \phi(u)= \begin{cases} \frac{e^u-1}{u} & \text{se $u\neq 0$},\\ 1 & \text{se $u=0$.} \end{cases} \] O vector normal unitario de $S$ é \[ \mathbf{N}_{\mathbf{x}(u,v)}=\frac{1}{\sqrt{2+e^{-2u}}}\bigl(1,-e^{-u},-1\bigr). \] Considérase o campo de vectores $\mathbf{V}(x,y,z)=(1,0,1)$.

• ¿Son as curvas $v$-paramétricas xeodésicas?
• Comprobar que o campo de vectores $\mathbf{V}$ é tanxente á superficie.
• Sexa $\alpha(t)=\mathbf{x}(t,0)$. Probar que $\mathbf{V}$ é paralelo ó longo de $\alpha$.
• Calcula-lo transporte paralelo ó longo de $\alpha$ do vector $(-1,-2,1)$ desde o punto $(0,0,1)$ ata o punto $(3/4, \log 2, 5/4)$.
• Calcular $\exp_p(\mathbf{w})$ sendo $p=(0,0,1)$ e $\mathbf{w}=(2,0,2)$.

Determinar se as seguintes afirmacións son verdadeiras ou falsas xustificando a resposta:

• Se $S$ é unha superficie isométrica á esfera unidade $\mathbb{S}^2(1)$, entón existe un movemento ríxido $F\colon\mathbb{R}^3\to\mathbb{R}^3$ tal que $F(S)=\mathbb{S}^2(1)$.
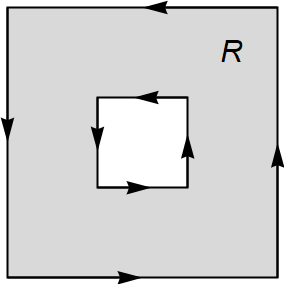
• Consideremos no plano a orientación dada polo sentido de xiro antihorario. Entón, o borde da rexión non simple $R$ da figura está orientado positivamente.
• Sexa $S$ unha superficie regular e $p\in S$. Entón, a aplicación exponencial $\exp_p$ define un difeomorfismo entre unha veciñanza aberta da orixe de $T_p S$ e unha veciñanza aberta de $p$ en $S$.
• Unha superficie con curvatura de Gauss $K=1$ é localmente isométrica á esfera unidade $\mathbb{S}^2(1)$.

Sexa $S$ a superficie definida pola parametrización \[ \mathbf{x}(u,v)=(u,\,v,\,uv),\quad u,v\in\R. \] Calcular, utilizando a fórmula de Gauss-Bonnet, a curvatura integral da rexión $R$ limitada polas curvas paramétricas \[ \begin{aligned} C_1\colon &{\ }u=0,\ 0\leq v\leq 1, & C_2\colon &{\ }u=1,\ 0\leq v\leq 1,\\ C_3\colon &{\ }v=0,\ 0\leq u\leq 1, & C_4\colon &{\ }v=1,\ 0\leq u\leq 1. \end{aligned} \]

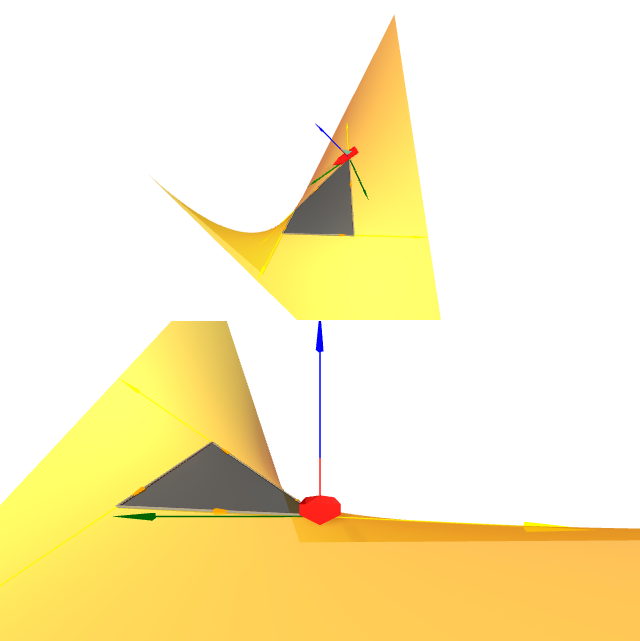
Probar que toda superficie regular compacta ten un punto elíptico (é dicir, un punto $p$ tal que $K(p)>0$).

Sexa $\gamma\colon I\to S$ unha xeodésica parametrizada por lonxitude de arco nunha superficie orientada $S$. Probar que $\bigl(\gamma'(t),J\gamma'(t)\bigr)$ é unha base ortonormal paralela positivamente orientada ó longo de $\gamma$.