Problemas da aplicación exponencial

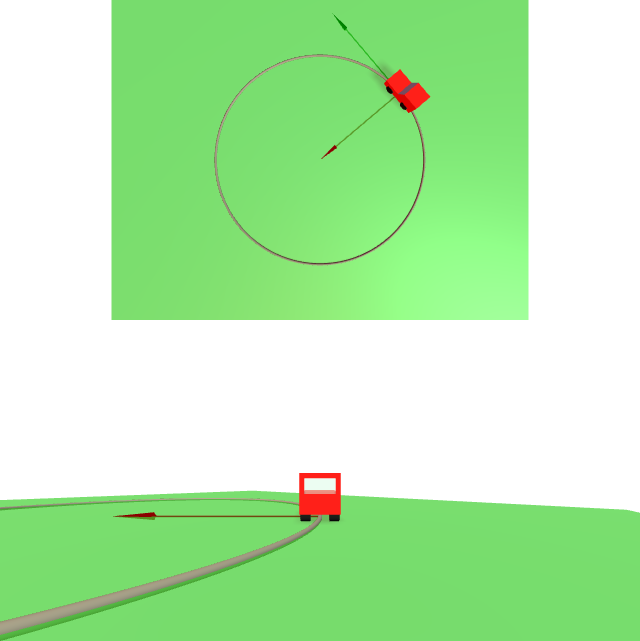
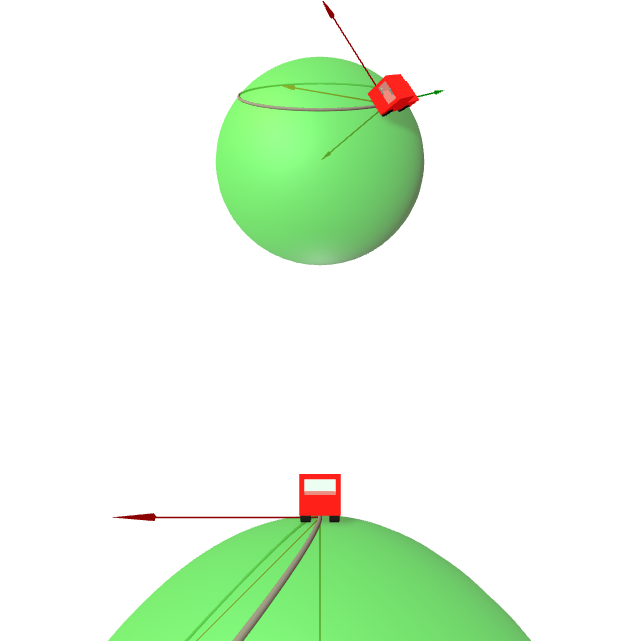
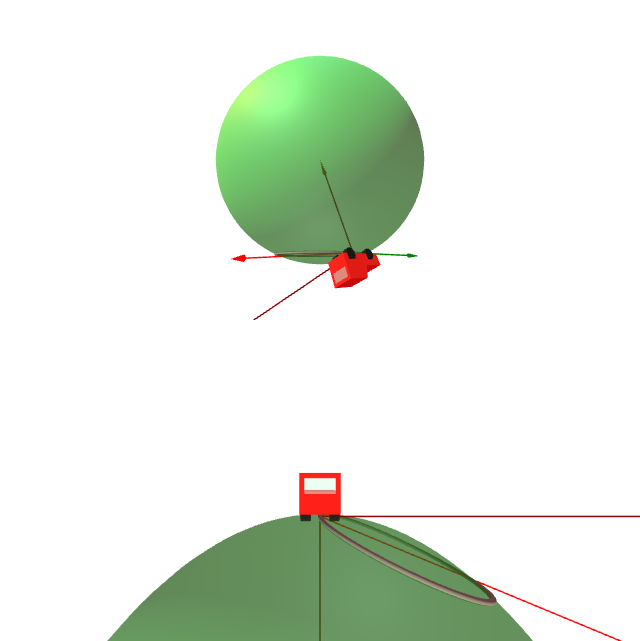
Na esfera unidade $\mathbb{S}^2(1)$, pídese calcular

1. $\exp_{p}(\vec{v})$, sendo $p\in\mathbb{S}^2(1)$ o punto ${p}=(1,0,0)$, e $\vec{v}\in T_p\mathbb{S}^2(1)$ o vector tanxente $\vec{v}=(0,0,-{\pi}/{2})$.
2. $\exp_{q}(0,{3\pi\sqrt{2}}/{8},-{3\pi\sqrt{2}}/{8})$, sendo ${q}=(0,{\sqrt{2}}/{ 2},{\sqrt{2}}/{2})$.
3. $\exp_{PN}({\pi\sqrt{2}}/{2},{\pi\sqrt{2}}/{2},0)$, sendo $PN$ o punto correspondente ó polo norte ${PN}=(0,0,1)$.

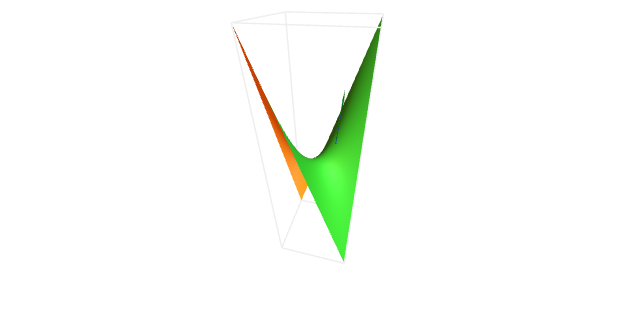
Dada a superficie $\mathbf{x}(u,v)=(u,v,u\,v)$, calcular $\exp_{p}(\vec{v})$ sendo ${p}=(1,1,1)$ e $\vec{v}=(0,3,3)$.

No toro de revolución parametrizado por \[ \mathbf{x}(u,v) =\left( (a+r\,\cos u)\cos v ,(a+r\,\cos u)\sin v, r\,\sin u\right), \] con $a >r > 0$, calcular $\exp_{(r+a,0,0)}(0,0,r\,\pi )$.

Sexa o cono parametrizado por $\mathbf{x}(u,v)=(a\, u\,\cos v ,a\, u\, \sin v ,b\,u)$. Determinar se está correctamente definido o punto $\exp_{p}(\vec{v})$, sendo ${p}=(a,0,b)$ e $\vec{v}=(-a,0,-b)$.

No elipsoide (de revolución) $x^2+y^2+\frac{z^2}{4}=1$, calcular $\exp_{(1,0,0)}(0,\frac{\pi}{2}, 0)$.

No cilindro circular recto parametrizado por \[ \mathbf{x}(u,v)=(\cos u,\sin u,v), \] con $-\pi<u,v<\pi$, calcular $\exp_{(1,0,0)}(0,\pi ,\pi )$.

Sexa o hiperboloide $x^2+y^2-z^2=1$, parametrizado (como superficie regrada) por \[ \mathbf{x}(s,v)=(\cos s -v\, \sin s ,\sin s+v\cos s, v), \] $-\pi < s < \pi$. Calcular $\exp_{(1,0,0)}(0,2,2)$.

Calcula-la lonxitude das circunferencias xeodésicas en superficies con curvatura de Gauss constante.

Calcula-la curvatura xeodésica das circunferencias xeodésicas en superficies con curvatura de Gauss constante.