Problemas do Teorema de Gauss-Bonnet

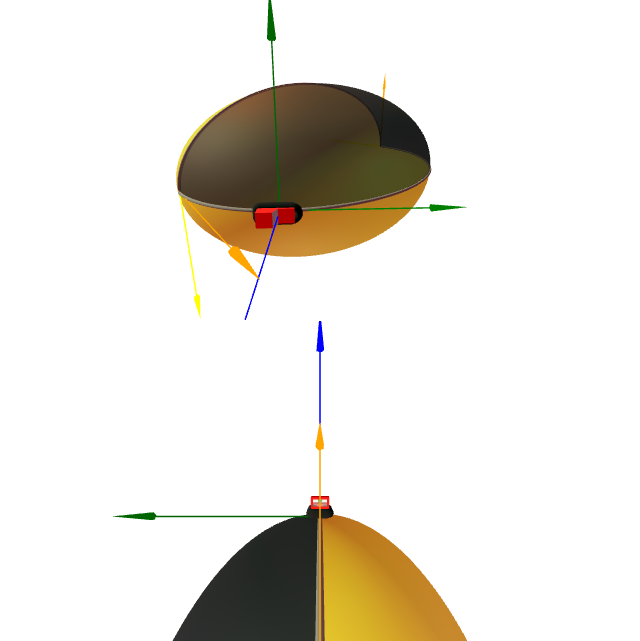
Sexa o toro de revolución de radios $0<r<a$ parametrizado por \[ \mathbf{x}(u,v)=((a+r\,\cos u)\cos v,(a+r\,\cos u)\sin v, r\, \sin u), \] con $-\pi<u,v<\pi$.

Parametriza-las liñas paramétricas. ¿Son xeodésicas?
Calcula-la curvatura integral da imaxen do polígono de lados $C_i$, $i=1,2,3,4$, onde: \[ \begin{aligned} C_1\colon& {\ }u=t,\ v=0, & & t\in [0,\frac{\pi}{2}],\\ C_2\colon& {\ }u=\frac{\pi}{2},\ v=t, & & t\in [0,\frac{\pi}{2}],\\ C_3\colon& {\ }u=\frac{\pi}{2}-t,\ v=\frac{\pi}{2}, && t\in [0,\frac{\pi}{2}],\\ C_4\colon & {\ }u=0,\ v=\frac{\pi}{2}-t, & & t\in [0,\frac{\pi}{2}]. \end{aligned} \]

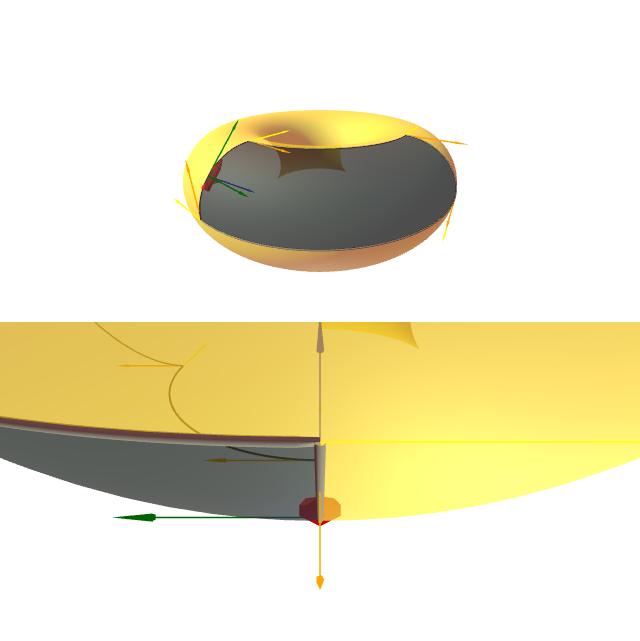
Sexa $\mathcal{S}$ o paraboloide $z=x^2+y^2$. Calcula-la curvatura integral da rexión $\mathfrak{R}$ limitada polas curvas \[ \begin{aligned} C_1\colon & {\ }z=1, && 0\leq y\leq 1,\\ C_2\colon & {\ }y=0, && 1\leq z\leq 4,\\ C_3\colon & {\ }z=4, && 0\leq y\leq 2. \end{aligned} \]

Problema de Gauss-Bonnet no paraboloide.

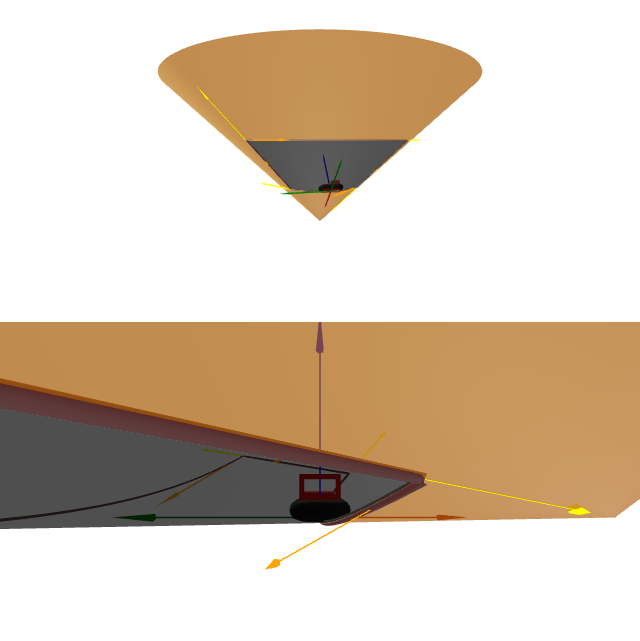
Sobre o cono parametrizado por $\mathbf{x}(u,v)=(a\, u\cos v ,a\, u \sin v , b\, u)$, con $a,b\in[1,+\infty)$, $u\in (0,\infty)$, $v\in(-\pi ,\pi)$, calcular tódolos termos da formula de Gauss-Bonnet para a rexión limitada polas curvas paramétricas \[ \begin{aligned} C_1\colon & {\ }u=1, && 0\leq v\leq{\pi}/{2},\\ C_2\colon & {\ }v=0, && 1\leq u\leq 2,\\ C_3\colon & {\ }u=2, && 0\leq v\leq{\pi}/{2},\\ C_4\colon & {\ }v={\pi}/{2}, && 1\leq u\leq2. \end{aligned} \]

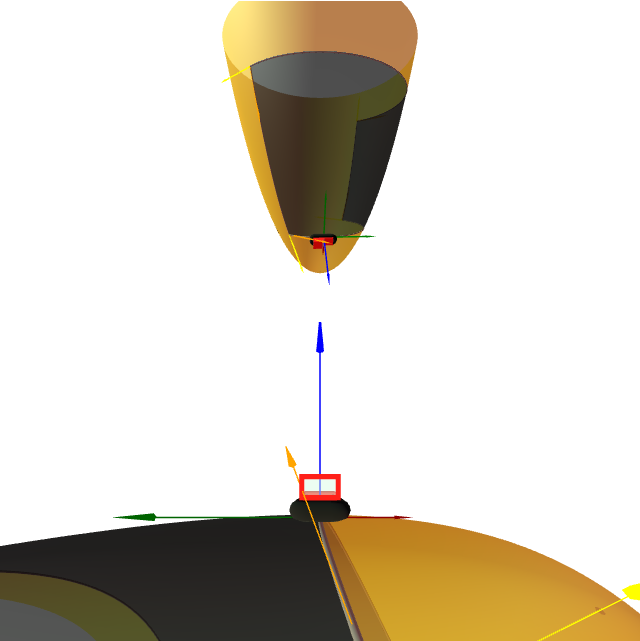
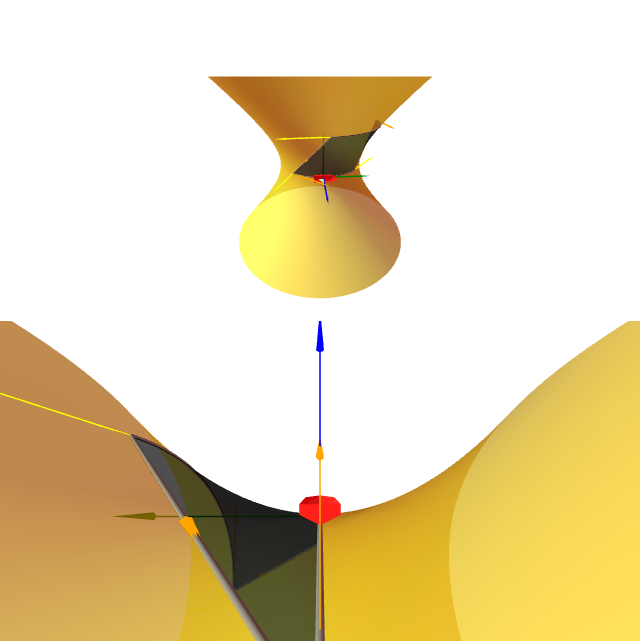
Sexa $\mathcal{S}$ o hiperboloide $x^2+y^2-z^2=1$. Sexa \[ \mathbf{x}(s,v)=(\cos s ,\sin s , 0)+v(-\sin s, \cos s, 1), \] $s\in (-\pi,\pi)$, $v\in \mathbb{R}$, unha parametrización de $\mathcal{S}$ como superficie regrada. Calcula-la curvatura integral da rexión $\mathfrak{R}$ limitada polas curvas paramétricas: \[ \begin{aligned} C_1\colon & {\ }v=0, && 0\leq s\leq{\pi}/{2},\\ C_2\colon & {\ }s={\pi}/{2}, && 0\leq v\leq 1,\\ C_3\colon & {\ }v=1, && 0\leq s\leq{\pi}/{2},\\ C_4\colon & {\ }s=0, && 0\leq v\leq 1. \end{aligned} \]

Problema de Gauss-Bonnet no hiperboloide.

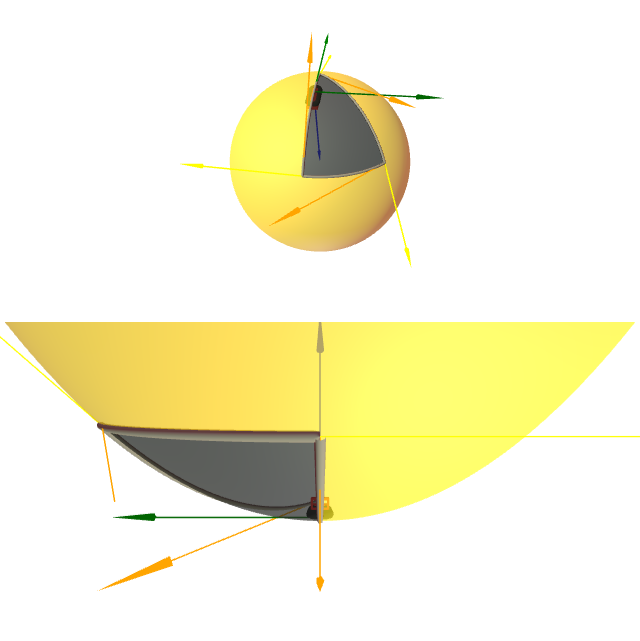
Sexa $\mathbb{S}^2(1)$ a esfera centrada na orixe e de radio $1$ parametrizada como $\mathbf{x}(\phi,\theta)=(\cos\phi\cos\theta,\cos\phi\sin\theta,\sin\phi)$. Calcula-la área da rexión $\mathfrak{R}$ delimitada polos puntos ${P}= (\frac{\sqrt{3}}{2},0,\frac{1}{2})$, ${Q}=(\frac{\sqrt{3}}{2\sqrt{2}},\frac{\sqrt{3}}{2\sqrt{2}},\frac{1}{2})$, ${N}=(0,0,1)$, e estando a fronteira de $\mathfrak{R}$ formada por curvas paramétricas da parametrización da esfera.

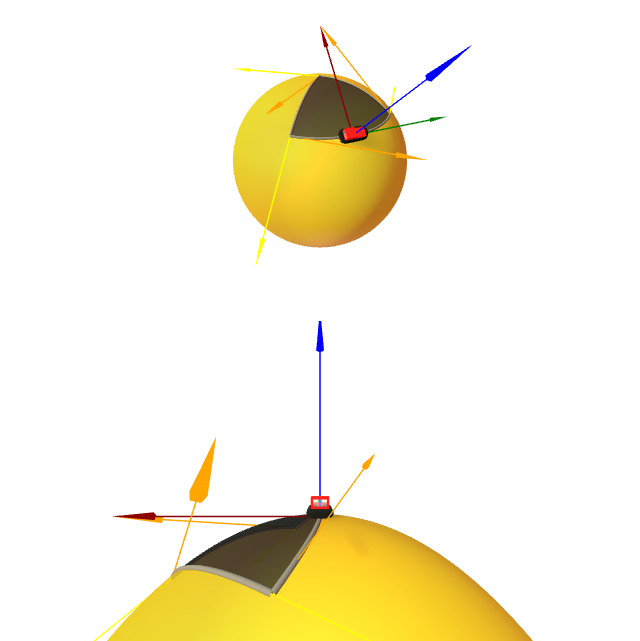
Sexa $\mathbb{S}^2(1)$ a esfera centrada na orixe e de radio $1$ parametrizada como $\mathbf{x}(\theta,\phi)=(\cos\theta\cos\phi,\sin\theta\cos\phi,\sin\phi)$. Calcula-la área da rexión $\mathfrak{R}$ delimitada polos puntos ${P}=(\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2})$, ${Q}=(0,\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$, ${N}=(0,0,1)$, e estando a fronteira de $\mathfrak{R}$ formada por curvas paramétricas da parametrización da esfera.

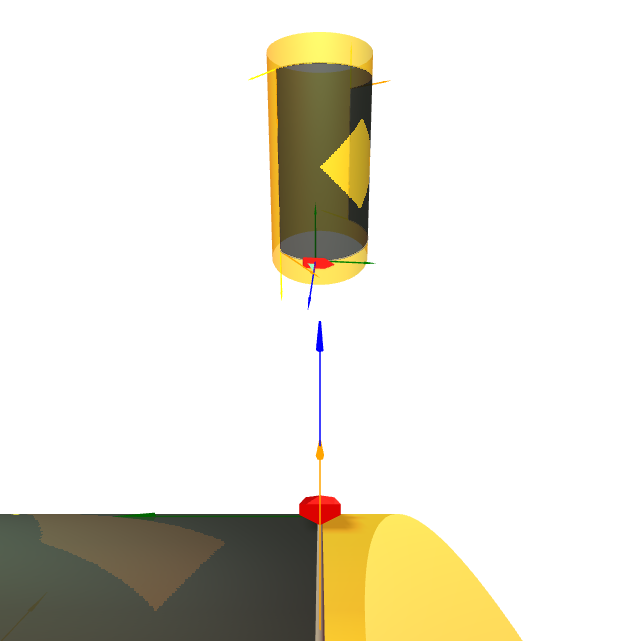
Sexa $\mathcal{S}$ o cilindro circular recto parametrizado mediante a fórmula \[ \mathbf{x}(u,v)=(\cos u,\sin u,v), \] $-\pi<u<\pi$, e $v\in\R$.

Obter tódolos termos do Teorema de Gauss-Bonnet na rexión $\mathbf{x}(\mathfrak{R})$, sendo $\mathfrak{R}$ a rexión do plano sombreada no plano $uv$ dado na figura. figura.

Problema de Gauss-Bonnet no cilindro. — Borde exterior do problema de Gauss-Bonnet no cilindro.

Sexa $\mathcal{S}$ o elipsoide \[ \left(\frac{x}{a}\right)^2+\left(\frac{y}{b}\right)^2 +\left(\frac{z}{c}\right)^2=1. \] Calcula-la curvatura integral da rexión $\mathfrak{R}$ limitada polas curvas \[ \begin{aligned} C_1\colon & {\ }z=0, && 0\leq y\leq b,\\ C_2\colon & {\ }y=0, && 0\leq z\leq c. \end{aligned} \]