Problemas de campos de vectores e orientación

Sexan $S=\{(x,y,z)\in \mathbb{R}^3 : x^4+y^4+z^4=1\}$, e $\mathbf{W}$ o campo de vectores en $\mathbb{R}^3$ determinado por $\mathbf{W}(x,y,z)=(-y^3,x^3,0)$. Mostrar que $S$ é unha superficie regular e probar que $\mathbf{W}$ é un campo de vectores tanxente a $S$.

Considéranse os campos de vectores en $\mathbb{R}^3$ definidos por \[ \begin{aligned} \mathbf{W}(x,y,z)&{}=(-y,x,0),\\[1ex] \mathbf{T}(x,y,z)&{}=(\rot\, \mathbf{W})(x,y,z). \end{aligned} \]

1. Probar que $\mathbf{W}$ e $\mathbf{T}$ son campos de vectores tanxentes ó cilindro $\{(x,y,z)\in\R^3:x^2+y^2=1\}$.
2. Representar graficamente estes campos sobre as curvas $v$-paramétricas do cilindro.
3. Probar que os fluxos de $\mathbf{W}$ e de $\mathbf{T}$ veñen dados por $\phi_t$ e $\psi_t$, respectivamente, onde \[ \begin{aligned} \phi_t(x,y,z) &{}=(x\cos t-y\sin t,\, x\sin t+y\cos t,\, z),\\[1ex] \psi_t(x,y,z) &{}=(x,y,z+2t). \end{aligned} \]

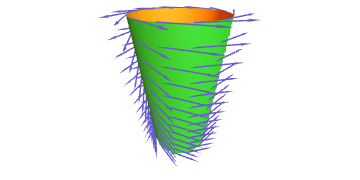
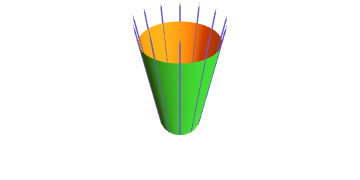
No conxunto aberto $\mathcal{U}=\{(x,y,z)\in \mathbb{R}^3 : z\neq 0\}$ considéranse os campos de vectores \[ \begin{aligned} \mathbf{X}(x,y,z) &{}=\Bigl(\frac{x}{z},\frac{y}{z},1\Bigr),\\[1ex] \mathbf{Y}(x,y,z) &{}=(\rot\, \mathbf{X})(x,y,z). \end{aligned} \]

1. Probar que $\mathbf{X}$ e $\mathbf{Y}$ son campos de vectores tanxentes ó cono, que se pode parametrizar como $\mathbf{x}(u,v)=(u\,\cos v,u\,\sin v,u)$.
2. Probar que o fluxo de $\mathbf{X}$ vén dado por $\phi_t(\mathbf{x}(u,v))=\mathbf{x}(u+t,v)$.
3. Calcula-lo fluxo de $\mathbf{Y}$.

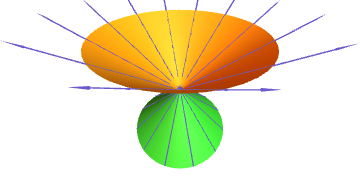
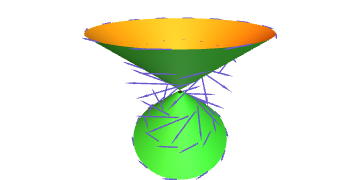
Probar que se unha superficie admite unha parametrización ortonormal (é dicir, $g_{11}=g_{22}=1$, $g_{12}=0$), entón a súa curvatura de Gauss é $K=0$ nesa veciñanza coordenada.

Probar que $S=\{(x,y,z)\in \mathbb{R}^3 : z-x^2y=0\}$ é unha superficie regular. Mostrar que é unha superficie orientable.

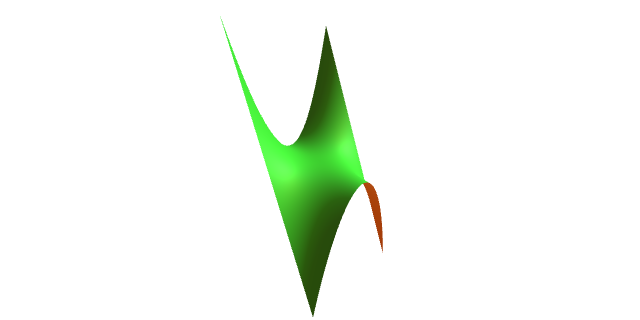
Considera-la superficie regular \[ S=\{(x,y,\cos x+\cos y)\in \mathbb{R}^3 : (x,y)\in (-2\pi,2\pi) \times (-2\pi,2\pi)\}. \] ¿É $S$ orientable?

Mostra que o grafo de calquera función diferenciable $f\colon U\subset\R^2\to\R$ é unha superficie orientable.

Proba que a superficie regular $S=\{(x,y,z)\in \mathbb{R}^3 : x^4+y^4+z^4=1\}$ é unha superficie orientable.

Probar que se $S$ é unha superficie regular, conexa e orientable, entón existen exactamente dous campos de vectores diferenciables, normais e unitarios definidos en $S$.

Mostrar que se $F\colon S_1 \to S_2$ é un difeomorfismo entre superficies regulares, entón $S_1$ é orientable se e só se $S_2$ é orientable.

Considerar unha superficie $S=S_1\cup S_2$, onde $S_1$ e $S_2$ son superficies orientables con intersección $S_1\cap S_2$ conexa. Probar que entón $S$ é orientable.

Sexa $S$ unha superficie regular cuberta por dous entornos coordenados conexos $\mathcal{V}_1$ e $\mathcal{V}_2$.

1. Mostrar que se a intersección $\mathcal{V}_1\cap\mathcal{V}_2$ ten unha única compoñente conexa, entón $S$ é orientable.
2. Mostrar que se $\mathcal{V}_1\cap\mathcal{V}_2$ ten dúas compoñentes conexas $\mathcal{W}^+$ e $\mathcal{W}^-$ e o jacobiano do cambio de coordenadas é positivo en $\mathcal{W}^+$ e negativo en $\mathcal{W}^-$, entón $S$ non é orientable.

Probar que un difeomorfismo entre superficies orientadas $f\colon S_1\to S_2$ preserva a orientación se e só se para cada parametrización positivamente orientada $\mathbf{x}\colon U\subset\R^2\to S_1$ de $S_1$, $f\circ\mathbf{x}$ é unha parametrización positivamente orientada de $S_2$.

Sexa $f\colon S_1\to S_2$ un difeomorfismo entre superficies orientadas, con $S_1$ conexa. Probar que $f$ preserva a orientación se e só se existe $p\in S_1$ tal que a diferencial $df_p\colon T_p S_1\to T_{f(p)}S_2$ preserva a orientación.

Sexa $S$ unha superficie orientada cun campo de vectores normal e unitario $\mathbf{N}$ positivamente orientado. Probar que unha base (ordeada) $(v_1,v_2)$ de $T_p S$ está positivamente orientada se e só se $\det(v_1,v_2,\mathbf{N}_p) > 0$.