A proba chi-cadrado
A proba chi-cadrado, ou proba $\chi^2$, é un contraste de hipóteses introducido por Pearson para determinar se a discrepancia entre as frecuencias esperadas e as frecuencias observadas nunha táboa de continxencia é estatisticamente significativa.
Neste capítulo, as variables estatísticas son discretas: só toman un número finito de valores, dividos en categorías. Distinguiremos dous tipos de tests, que computacionalmente son practicamente iguais, pero que conceptualmente son un pouco distintos.
Contrastes de independencia
Supoñamos que nunha poboación estamos interesados en observar dúas características $X$ e $Y$ que se corresponden con datos categóricos, é dicir, que son datos nominais que soamente poden tomar valores concretos, chamados categorías. Cada valor está nunha, e só nunha, categoría (é dicir, as categorías son disxuntas). Poñamos que $X$ pode tomar $f$ valores distintos $A_1,\dots,A_f$, e que $Y$ pode tomar $c$ valores $B_1,\dots,B_c$. O problema ó que nos enfrentamos agora é o de determinar se as dúas características $X$ e $Y$ son ou non independentes. De feito, o que queremos é ver se hai (ou non) evidencia significativa de que as dúas características non son independentes.
Tomamos unha mostra aleatoria simple bidimensional (é dicir, medindo as dúas características) na poboación, $(X_1,Y_1),\dots,(X_n,Y_n)$. Denotamos por $n_{ij}$ ó número de observacións na mostra de tal xeito que o valor de $X$ se atopa en $A_i$ e o valor de $Y$ en $B_j$. Os valores poden por tanto dispoñerse nunha táboa de continxencia, que consiste en organiza-los datos do seguinte xeito:
| $X$ \ $Y$ | $B_1$ | $B_2$ | $\dots$ | $B_c$ | $\Sigma$ |
|---|---|---|---|---|---|
| $A_1$ | $n_{11}$ | $n_{12}$ | $\dots$ | $n_{1c}$ | $n_{1\boldsymbol{\cdot}}$ |
| $A_2$ | $n_{21}$ | $n_{22}$ | $\dots$ | $n_{2c}$ | $n_{2\boldsymbol{\cdot}}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | |
| $A_f$ | $n_{f1}$ | $n_{f2}$ | $\dots$ | $n_{fc}$ | $n_{f\boldsymbol{\cdot}}$ |
| $\Sigma$ | $n_{\boldsymbol{\cdot}1}$ | $n_{\boldsymbol{\cdot}2}$ | $\dots$ | $n_{\boldsymbol{\cdot}c}$ | $n$ |
Nesta táboa empregouse a notación: \[ \begin{aligned} n_{i\boldsymbol{\cdot}} & {}= n_{i1}+n_{i2}+\dots+n_{ic},\\[1ex] n_{\boldsymbol{\cdot}j} & {}= n_{1j}+n_{2j}+\dots+n_{fj}, \end{aligned} \] que son os números totais de observacións que se atopan nos conxuntos $A_i$ e $B_j$ respectivamente. Obviamente, $n_{1\boldsymbol{\cdot}}+\dots+n_{f\boldsymbol{\cdot}}= n_{\boldsymbol{\cdot}1}+\dots+n_{\boldsymbol{\cdot}c}=n$.
As probabilidades reais da poboación son denotadas como \[ p_{ij}=P\bigl((X\in A_i)\cap (Y\in B_j)\bigr), \] e así, por se-las categorías disxuntas, \[ \begin{aligned} p_{i\boldsymbol{\cdot}}=P(X\in A_i) & {}= p_{i1}+p_{i2}+\dots+p_{ic},\\[1ex] p_{\boldsymbol{\cdot}j}=P(Y\in B_j) & {}= p_{1j}+p_{2j}+\dots+p_{fj}. \end{aligned} \] Isto podería organizarse tamén nunha táboa de probabilidades:
| $X$ \ $Y$ | $B_1$ | $B_2$ | $\dots$ | $B_c$ | $\Sigma$ |
|---|---|---|---|---|---|
| $A_1$ | $p_{11}$ | $p_{12}$ | $\dots$ | $p_{1c}$ | $p_{1\boldsymbol{\cdot}}$ |
| $A_2$ | $p_{21}$ | $p_{22}$ | $\dots$ | $p_{2c}$ | $p_{2\boldsymbol{\cdot}}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | |
| $A_f$ | $p_{f1}$ | $p_{f2}$ | $\dots$ | $p_{fc}$ | $p_{f\boldsymbol{\cdot}}$ |
| $\Sigma$ | $p_{\boldsymbol{\cdot}1}$ | $p_{\boldsymbol{\cdot}2}$ | $\dots$ | $p_{\boldsymbol{\cdot}c}$ | $1$ |
En caso de que as dúas características fosen realmente independentes, teriamos \[ p_{ij}=P\bigl((X\in A_i)\cap (Y\in B_j)\bigr)=P(X\in A_i)P(Y\in B_j) =p_{i\boldsymbol{\cdot}}\,p_{\boldsymbol{\cdot}j} \] para calquera para $i$, $j$. En consecuencia, o contraste de hipóteses que pretendemos estudar é: \[ H_0\colon\ p_{ij}=p_{i\boldsymbol{\cdot}}\,p_{\boldsymbol{\cdot}j},\quad \forall i\in\{1,\dots,f\},\, \forall j\in\{1,\dots,c\}. \]
Por tanto, o que resta por facer é estima-las probabilidades $p_{ij}$ e atopar un estatístico convinte que nos permita decidir se cos valores da mostra podemos ou non descartar $H_0$.
A partir da mostra, os estimadores obvios das probabilidades son \[ \begin{aligned} \widehat{p_{ij}} & {}=\frac{n_{ij}}{n}, & \widehat{p_{i\boldsymbol{\cdot}}} & {}=\frac{n_{i\boldsymbol{\cdot}}}{n}, & \widehat{p_{\boldsymbol{\cdot}j}} & {}=\frac{n_{\boldsymbol{\cdot}j}}{n}. \end{aligned} \]
Por outra banda, baixo a hipótese de independencia, o valor da celda $(i,j)$ da táboa de continxencia debería ser \[ E_{ij}=np_{ij}=n\,p_{i\boldsymbol{\cdot}}\,p_{\boldsymbol{\cdot}j}, \] que por tanto se estima por \[ \widehat{E_{ij}}=n\,\widehat{p_{i\boldsymbol{\cdot}}}\,\widehat{p_{\boldsymbol{\cdot}j}} =\frac{{n_{i\boldsymbol{\cdot}}}\,{n_{\boldsymbol{\cdot}j}}}{n}. \]
Para determinar se os $n_{ij}$ están suficientemente próximos a $\widehat{E_{ij}}$, empregámo-lo estatístico \[ \sum_{i,j}\frac{(n_{ij}-\widehat{E_{ij}})^2}{\widehat{E_{ij}}}\sim \chi^2_{(f-1)(c-1)}, \] que segue aproximadamente unha distribución $\chi^2$ de Pearson con $(f-1)(c-1)$ graos de liberdade cando a mostra é suficientemente grande.
Este contraste é unilateral dereito, así que para un nivel de significación $\alpha$, temos
- Rexión crítica: $(\chi^2_{(f-1)(c-1),\,\alpha},\,\infty)$.
- Rexión de aceptación: $[0,\chi^2_{(f-1)(c-1),\,\alpha}]$.
Obviamente, tamén se podería calcula-lo valor $P$ e rexeita-la hipótese nula cando este valor sexa moi pequeno.
Realízase un estudo para investiga-la asociación entre a cor e a fragancia das azaleas silvestres. Obsérvanse 200 prantas floridas seleccionadas aleatoriamente, e clasifícase cada unha delas segundo a cor e a presencia de fragancia.
| fragancia \ cor | branca | rosa | naranxa |
|---|---|---|---|
| si | 12 | 60 | 58 |
| non | 50 | 10 | 10 |
¿Hai probas significativas de asociación entre a cor das flores e a súa fragancia?
Denotemos por $X$ a fragancia dunha azalea, e por $Y$ a súa cor. En primeiro lugar construímo-la táboa de continxencia:
| fragancia \ cor | branca | rosa | naranxa | $\Sigma$ |
|---|---|---|---|---|
| si | 12 | 60 | 58 | 130 |
| non | 50 | 10 | 10 | 70 |
| $\Sigma$ | 62 | 70 | 68 | 200 |
O problema consiste en facer un contraste de hipóteses de independencia para datos categóricos, é dicir, \[ H_0\colon p_{ij}=p_{i\cdot}p_{\cdot j},\quad \forall i\in\{1,2\},\ \forall j\in\{1,2,3\}. \]
Veremos máis adiante que a razón de que este sexa un contraste de independencia é que o investigador simplemente clasifica os datos do total da mostra en dúas categorías (neste caso, fragancia e cor das azaleas).
Para resolve-lo problema, calculámo-los valores esperados, no suposto de que houbese independencia das variables, mediante a fórmula $\widehat{E_{ij}} =\frac{n_{i\boldsymbol{\cdot}}n_{\boldsymbol{\cdot}j}}{n}$ (en verde), e tamén os valores $(n_{ij}-\widehat{E_{ij}})^2/\widehat{E_{ij}}$ (en vermello), obtendo:
| fragancia \ cor | branca | rosa | naranxa | $\Sigma$ |
|---|---|---|---|---|
| si | 12 40.3 19.87 |
60 45.5 4.62 |
58 44.2 4.31 |
130 |
| non | 50 21.7 36.91 |
10 24.5 8.58 |
10 23.8 8.00 |
70 |
| $\Sigma$ | 62 | 70 | 68 | 200 |
Finalmente aprovéitanse todos estes cálculos para determina-lo valor no estatístico, (que consiste en suma-los valores vermellos), para obter 82.29.
O estatístico segue unha distribución $\chi^2$ con $(2-1)(3-1)=2$ graos de liberdade. Xa que non nos dan un nivel de significación, calculámo-lo valor $P$ como $P=P(\chi^2_2\geq 82.29)<0.001$. (Utilizando software informático obtense $P=1.35\cdot 10^{-18}$.)
Conclusión: rexeitámo-la hipótese nula, e concluímos que si hai evidencia significativa, cun nivel de confianza moi alto (maior có 99.9%), de que existe relación entre a cor da flor e a súa fragancia.
Contrastes de homoxeneidade
Este contraste é bastante parecido ó da sección anterior, polo menos no que a cálculos se refire, anque o obxectivo é bastante distinto.
Supoñamos que temos $f$ poboacións nas que se observa unha determinada característica que pode tomar un valor de entre $c$ valores distintos $A_1,\dots,A_c$. O problema ó que nos enfrentamos é o de determinar se a distribución de probabilidade desa característica é a mesma en todas esas poboacións, ou se polo contrario, ditas poboacións son heteroxéneas con distintas distribucións de probabilidade.
Tomamos unha mostra aleatoria simple en cada unha das poboacións, con tamaños $n_1,\dots,n_f$, respectivamente. Denotamos por $n_{ij}$ o número de observacións na mostra $i$ que se atopa en $A_j$. Os datos poden dispoñerse nunha táboa de continxencia, organizada do seguinte xeito:
| Mostra | $A_1$ | $A_2$ | $\dots$ | $A_c$ | tamaño |
|---|---|---|---|---|---|
| 1 | $n_{11}$ | $n_{12}$ | $\dots$ | $n_{1c}$ | $n_{1}$ |
| 2 | $n_{21}$ | $n_{22}$ | $\dots$ | $n_{2c}$ | $n_{2}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | |
| f | $n_{f1}$ | $n_{f2}$ | $\dots$ | $n_{fc}$ | $n_{f}$ |
| $\Sigma$ | $n_{\boldsymbol{\cdot}1}$ | $n_{\boldsymbol{\cdot}2}$ | $\dots$ | $n_{\boldsymbol{\cdot}c}$ | $n$ |
De novo empregouse a notación: \[ \begin{aligned} n_{\boldsymbol{\cdot}j} & {}= n_{1j}+n_{2j}+\dots+n_{fj}, \end{aligned} \] que son os números totais de observacións que se atopan nos conxuntos $A_i$. Ademais, $n=n_1+\dots+n_f$ é o tamaño que se obtén ó xuntar tódalas mostras.
A hipótese de homoxeneidade significa que cada conxunto $A_j$ ten unha probabilidade $p_j$ independente da poboación $i$. Por tanto, se $p_{ij}$ é a probabilidade de $A_j$ na poboación $i$, a hipótese nula é \[ H_0\colon\, p_{1j}=p_{2j}=\dots=p_{fj}\, (=p_j),\quad \forall j\in\{1,\dots,c\}. \]
As probabilidades $p_j$ poden estimarse mediante \[ \widehat{p_j}=\frac{n_{\boldsymbol{\cdot}j}}{n}. \] Baixo a hipótese de homoxeneidade, a frecuencia teórica de $A_j$ na poboación $i$ é \[ E_{ij}=n_i p_j, \] que por tanto se estima mediante \[ \widehat{E_{ij}}=\frac{n_i n_{\boldsymbol{\cdot}j}}{n}. \]
Para determinar se os $n_{ij}$ están suficientemente próximos a $\widehat{E_{ij}}$ empregámo-lo estatístico \[ \sum_{i,j}\frac{(n_{ij}-\widehat{E_{ij}})^2}{\widehat{E_{ij}}}\sim \chi^2_{(f-1)(c-1)}, \] que segue aproximadamente unha distribución $\chi^2$ de Pearson con $(f-1)(c-1)$ graos de liberdade.
Este contraste é unilateral dereito, así que para un nivel de significación $\alpha$, temos
- Rexión crítica: $(\chi^2_{(f-1)(c-1),\,\alpha},\,\infty)$.
- Rexión de aceptación: $[0,\chi^2_{(f-1)(c-1),\,\alpha}]$.
O contraste de independencia e o contraste de homoxeneidade son moi similares en canto a cálculos e interpretación. A diferencia fundamental está no xeito de selecciona-las mostras, xa que no contraste de homoxeneidade, o tamaño das mostras (é dicir, o total das filas) está fixado polo experimentador, mentres que no contraste de independencia é arbitrario.
Para probar unha nova vacina contra a hepatite, tómanse 549 voluntarios ós que se lles administra a vacina, e 534 ós que non. Ó cabo dun tempo obsérvanse os seguinte casos de enfermidade:
| mostra | ten hepatite | tamaño |
|---|---|---|
| vacinado | 11 | 549 |
| non vacinado | 70 | 534 |
¿É a vacina eficaz?
Para ver se a vacina é eficaz temos que dar evidencia significativa de que a proporción de enfermos de hepatite é menor na poboación dos vacinados. Por tanto, é un contraste de hipóteses sobre homoxeneidade no que pretendemos refuta-la hipótese nula de que a distribución de probabilidade do número de enfermos de hepatite é a mesma para as dúas poboacións.
En primeiro lugar completámo-la táboa de continxencia:
| hepatite si | hepatite non | tamaño | |
|---|---|---|---|
| vacinado | 11 | 538 | 549 |
| non vacinado | 70 | 464 | 534 |
| $\Sigma$ | 81 | 1002 | 1083 |
Temos que facer un contraste de hipóteses de homoxeneidade para datos categóricos: \[ H_0\colon p_{11}=p_{21},\ p_{12}=p_{22}. \]
A continuación calculámo-los valores esperados no suposto de que houbese homoxeneidade nas poboacións mediante a fórmula $\widehat{E_{ij}} =\frac{n_{i}n_{\boldsymbol{\cdot}j}}{n}$ (en verde), e tamén os valores $(n_{ij}-\widehat{E_{ij}})^2/\widehat{E_{ij}}$ (en vermello), obtendo:
| vacinado \ hepatite | si | non | tamaño |
|---|---|---|---|
| si | 11 41.06 22.01 |
538 507.94 1.78 |
549 |
| non | 70 39.94 22.63 |
464 494.06 1.83 |
534 |
| $\Sigma$ | 81 | 1002 | 1083 |
Finalmente aprovéitanse todas estes contas para calcula-lo valor no estatístico, (que consiste en suma-los valores vermellos), para obter 48.24.
O estatístico segue unha distribución $\chi^2$ con $(2-1)(2-1)=1$ grao de liberdade. Xa que non nos dan un nivel de significación, calculámo-lo valor $P$ como $P=P(\chi^2_1\geq 48.24)<0.001$. (Empregando software informático obtense $P=3.7\cdot 10^{-12}$.)
Conclusión: rexeitámo-la hipótese nula, e concluímos que hai evidencia significativa, cun nivel de confianza superior ó 99.9%, de que a proporción de enfermos de hepatite é distinta dependendo de se estamos na poboación de individuos vacinados ou non vacinados.
En realidade, este contraste de hipóteses non serve para determinar se o medicamento é eficar ou non. Non obstante, tendo en conta os datos da táboa, onde se observa que a proporción de enfermos de hepatite na poboación dos individuos vacinados é menor cá esperada, podemos concluír que a vacina é eficaz.
Os contrastes de independencia e homoxeneidade son bastante populares e empréganse a miúdo como estudos preliminares para ver se hai relación entre dúas ou máis variables. Nótese non obstante, que estes contrastes non nos din cal é a relación entre as variables, aínda que mirando os valores da táboa podemos sacar algunha conclusión. Para atopar unha relación que explique como se relaciona unha variable con outra necesítanse outras técnicas estatísticas como a regresión.
É moi típico que, por erro, descoñecemento, ou por tratar de influencia-la opinión da xente, se extraian dun test deste estilo conclusións distintas (aínda que aparentemente relacionadas) ás que en realidade se fan no estudo. Tamén é típico extrapolar causalidade (un suceso implica outro), cando só hai correlación (dous sucesos pasan ó mesmo tempo).
Realízase un estudo de mercado consistente en clasifica-la poboación de acordo co seu poder adquisitivo en nivel alto, medio e baixo. Tómase unha mostra de 50 persoas de cada clase social e mírase se posúen un reloxio de marca Rolex. Constátase que da clase alta teñen un 30 persoas, 14 de clase media, e 5 de clase baixa.
- Realiza-lo correspondente contraste de hipóteses para ver se existe relación entre a clase social e ser posuidor dun Rolex.
- ¿Podemos afirmar que hai evidencia estatística de que mercar un Rolex aumenta o poder adquisitivo?
Temos 3 poboacións, dependendo do "poder adquisitivo", e a variable aleatoria $Y$="ter un Rolex".
En primeiro lugar construímo-la táboa de continxencia:
| renta \ Rolex | si | non | tamaño |
|---|---|---|---|
| alta | 30 | 20 | 50 |
| media | 14 | 36 | 50 |
| baixa | 5 | 45 | 50 |
| $\Sigma$ | 49 | 101 | 150 |
Temos que face-lo contraste de hipóteses: \[ H_0\colon p_{11}=p_{21}=p_{31}, p_{12}=p_{22}=p_{32}. \]
Este é un contraste de hipóteses para homoxeneidade de datos categóricos, xa que o tamaño da mostra en cada poboación é fixado polo investigador. Para iso empregámo-lo estatístico \[ \sum_{i,j} \frac{\bigl(n_{ij}-\widehat{E_{ij}}\bigr)^{2}}{\widehat{E_{ij}}}, \] que segue unha distribución $\chi^2$ de Pearson con $(f-1)(c-1)$ graos de liberdade.
O número de graos de liberdade da distribución é $(3-1)(2-1)=2$.
A continuación calculámo-las frecuencias esperadas, no suposto de que a hipótese nula sexa certa, mediante a fórmula $\widehat{E_{ij}}=\frac{n_{i\boldsymbol{\cdot}}n_{\boldsymbol{\cdot}j}}{n}$:
| renta \ Rolex | si | non | tamaño |
|---|---|---|---|
| alta | 16.33 | 33.67 | 50 |
| media | 16.33 | 33.67 | 50 |
| baixa | 16.33 | 33.67 | 50 |
| $\Sigma$ | 49 | 101 | 150 |
Agora calculámo-los valores intermedios do estatístico $(n_{ij}-\widehat{E_{ij}})^2/\widehat{E_{ij}}$:
| renta \ Rolex | si | non | $\Sigma$ |
|---|---|---|---|
| alta | 11.435 | 5.548 | |
| media | 0.333 | 0.162 | |
| baixa | 7.864 | 3.815 | |
| $\Sigma$ | 29.157 |
A suma dos valores intermedios, que coincide co valor no estatístico, é 29.157.
Calculámo-lo valor $P$ como $P=P(\chi^2_{2} > 29.157)=0.5\cdot 10^{-6}$, que é un valor pequeno.
Conclusión: Rexeitamos $H_0$, e concluímos que hai evidencia significativa, cun nivel de confianza moi elevado, de que ter un Rolex depende do poder adquisitivo da persoa.
Non obstante, os datos que se dan neste exercicio non están encamiñados a responde-la segunda pregunta. Podemos deducir que hai relación entre "ter poder adquisitivo alto" e "ter un Rolex", pero non podemos dicir nada con respecto á relación entre mercar un Rolex
e aumenta-lo poder adquisitivo
.
Aínda que a lóxica indica a pensar que a resposta á segunda pregunta é negativa, os datos do problema non o confirman nin o refutan.
Bondade do axuste
Ata agora os contrastes de hipóteses foron empregados para decidi-la veracidade dunha hipótese sobre os parámetros dunha distribución. En ocasións, non obstante, é necesario emitir un xuízo sobre a distribución poboacional no seu conxunto. O problema da bondade do axuste consiste en decidir, á vista dos datos dunha mostra aleatoria simple dunha poboación, se pode admitirse que a distribución poboacional coincide cunha certa distribución dada (no noso caso unha $N(0,1)$). Nótese que este é un problema non paramétrico.
Supoñamos que queremos averiguar se a distribución $F$ dunha poboación se axusta a unha distribución normal $N(\mu,\sigma)$. Supoñemos que temos unha mostra aleatoria simple $X_1,\dots,X_n$. O noso contraste é por tanto \[ \begin{aligned} H_0\colon F &{}=N(\mu,\sigma), & H_1\colon F &{}\neq N(\mu,\sigma). \end{aligned} \]
En primeiro lugar teremos que estima-los valores dos parámetros. Empregaremos para iso os estimadores insesgados $\hat{\mu}=\overline{X}$ e $\hat{\sigma}=s_{n-1}$.
O segundo paso deste contraste consiste en agrupa-los datos en intervalos. Para iso realízase o seguinte procedemento:
- Busca-los valores máis pequeno e máis grande. Tomar valores "redondos" un pouco máis pequenos có máis pequeno, e un pouco máis grande có máis grande tendo en conta a precisión dos datos.
- Decidir cantos intervalos se van empregar. Dividiranse os datos en intervalos do mesmo tamaño (preferentemente os extremos deberían ser enteiros, ou números "redondos"). Hai varias regras para decidir este número. Unha posibilidade é tomar aproximadamente $\sqrt{n}$ intervalos. É conveniente que cada intervalo resultante teña polo menos 5 valores. O número de tales intervalos denotámolo por $r$.
- Calcula-los límites dos intervalos tendo en conta os datos anteriores.
- Face-lo reconto de valores en cada intervalo.
Unha vez que témo-los datos divididos en intervalos, podemos calcula-la frecuencia observada $o_i$ destes en cada intervalo. Este datos compáranse coa probabilidade de que a distribución $N(\mu,\sigma)$ estea entre cada un dos valores dos intervalos, multiplicada por $n$. Isto é o que se chama a frecuencia teórica $e_i$. Utilízase para iso a estimación de $\mu$ e $\sigma$.
Para decidir se as discrepancias entre as frecuencias mostrais e as teóricas son significativas, emprégase a proba $\chi^2$ de Pearson. Tomamos por tanto o estatístico \[ \chi^2_{r-k-1}=\sum_{i=1}^r\frac{(o_i-e_i)^2}{e_i}, \] que segue unha distribución $\chi^2$ de Pearson con $r-k-1$ graos de liberdade, onde $k$ é o número de parámetros que tivemos que estimar para precisa-la distribución teórica (se son $\mu$ e $\sigma$, entón $k=2$).
O estatístico anterior úsase para facer un contraste unilateral dereito.
Unha máquina produce pezas cunha determinada lonxitude, a cal se quere saber se segue unha distribución normal. Obtense a seguinte mostra:
| 10.39 | 10.66 | 10.12 | 10.32 | 10.25 | 10.91 | 10.52 | 10.83 | 10.72 | 10.28 |
| 10.35 | 10.46 | 10.54 | 10.72 | 10.23 | 10.18 | 10.62 | 10.49 | 10.32 | 10.61 |
| 10.64 | 10.23 | 10.29 | 10.78 | 10.81 | 10.39 | 10.34 | 10.62 | 10.75 | 10.34 |
| 10.41 | 10.81 | 10.64 | 10.53 | 10.31 | 10.46 | 10.47 | 10.43 | 10.57 | 10.74 |
Deséxase saber se esta mostra avala a hipótese de que a máquina produce pezas cunha lonxitude que efectivamente é normal.
Sexa $X$ a variable aleatoria "lonxitude das pezas que produce a máquina".
Vemos que temos $n=40$ datos. En primeiro lugar estimamos puntualmente a media e a desviación típica. Para iso obtemos $\overline{X}=10.502$ e $s_{n-1}=0.205$.
Trátase por tanto do contraste de hipóteses \[ \begin{aligned} H_0\colon F &{}=N(\overline{X},s_{n-1}), & H_1\colon F &{}\neq N(\overline{X},s_{n-1}), \end{aligned} \] pero agora non contrastamos ou estimámo-lo valor dos parámetros, se non o feito de que a distribución sexa ou non normal.
Para face-lo contraste de $\chi^2$ de bondade de axuste, primeiramente temos que dividi-lo percorrido dos valores en intervalos. Como hai 40 datos, dividimos en $7$ intervalos, o que é aproximadamente $\sqrt{40}$. O mínimo é $10.12$ e o máximo $10.91$. Podemos tomar como rango $[10,11]$ e dividilo en 7. Isto dá $(11-10)/7=0.1428$, así que redondeamos a $0.15$ e repartímo-lo exceso $0.15\cdot 7-1=0.05$ a cada lado. Así, os intervalos serían:
| (9.975, 10.125] | (10.125, 10.275] | (10.275, 10.425] |
| (10.425, 10.575] | (10.575, 10.725] | (10.725, 10.875] |
| (10.875, 11.025] |
A continuación contámo-lo número de elementos en cada subintervalo:
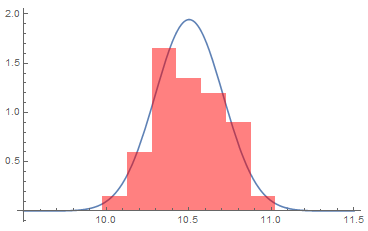
| Intervalo | $o_i$ |
|---|---|
| (9.975, 10.125] | 1 |
| (10.125, 10.275] | 4 |
| (10.275, 10.425] | 11 |
| (10.425, 10.575] | 9 |
| (10.575, 10.725] | 8 |
| (10.725, 10.875] | 6 |
| (10.875, 11.025] | 1 |
Temos $r=7$. Ademais, co propósito de comparar coa distribución teórica, que é unha normal $N(10.502,\,0.205)$, temos que toma-las colas ata $-\infty$ e $+\infty$. Completámo-la última columna cos valores teóricos $e_i$, que corresponden coa probabilidade de que a distribución estea no intervalo, multiplicada por $n$.
| Intervalo | $o_i$ | $e_i$ |
|---|---|---|
| $(-\infty, 10.125]$ | 1 | 1.3223 |
| $(10.125, 10.275]$ | 4 | 4.04803 |
| $(10.275, 10.425]$ | 11 | 8.77801 |
| $(10.425, 10.575]$ | 9 | 11.4123 |
| $(10.575, 10.725]$ | 8 | 8.89851 |
| $(10.725, 10.875]$ | 6 | 4.16001 |
| $(10.875, \infty]$ | 1 | 1.38084 |
| $\Sigma$ | 40 | 40. |
Unha vez temos tódolos datos, só queda substituír no estatístico de contraste con $k=2$, $r=7$. Este estatístico segue unha distribución $\chi^2$ con $r-k-1=4$ graos de liberdade. Así \[ \sum_{i=1}^7\frac{(o_i-e_i)^2}{e_i}=2.16109, \] e obtemos $P(\chi^2_4\geq 2.16109)=0.706158$, que é un valor moi alto.
Conclusión: aceptámo-la hipótese de que a lonxitude das pezas da máquina segue unha distribución normal.