Comparación de dúas poboacións
Neste capítulo centrarémosnos no problema de comparar dúas poboacións. A situación xeral é que temos dúas poboacións de interese, e en ambas se trata de estuda-la mesma característica. A cuestión é que as dúas poboacións se atopan, por así dicilo, en circunstancias distintas, e interesa comparalas para saber como afectan esas circunstancias particulares á medida da característica que se estuda. Colleremos unha mostra aleatoria simple en cada unha desas poboacións, e a partir delas, trataremos de tomar unha decisión sobre a característica que estamos estudando.
En principio preséntanse dúas posibilidades para as mostras: que sexan independentes, ou que estean emparelladas.
Se as mostras son independentes, entón temos dúas poboacións para as cales estudamos respectivamente dúas variables aleatorias $X$ e $Y$ independentes cunhas distribucións de probabilidade que pertencen á mesma familia.
Extraemos unha mostra aleatoria simple $X_1,\dots,X_{n_1}$ da primeira poboación, e outra $Y_1,\dots,Y_{n_2}$ da segunda. Supoñemos que as dúas mostras son independentes, é dicir, que os obxectos ou individuos da mostra da primeira poboación non teñen relación algunha cos da segunda. Nótese que os tamaños mostrais $n_1$ e $n_2$ non teñen por que ser iguais.
Cando as mostras están emparelladas, o procedemento é distinto e tratarase máis adiante neste capítulo.
Comparación das medias de dúas poboacións: mostras independentes
Supoñamos que $X$ e $Y$ seguen as dúas unha distribución normal, $N(\mu_1,\sigma_1)$ e $N(\mu_2,\sigma_2)$, respectivamente. Un xeito de compara-las medias poboacionais é restalas e compara-la súa diferencia. (Aínda que as distribucións non sexan normais, se a mostra é suficientemente grande recordemos que podemos asumi-los resultados que seguen en virtude do teorema central do límite.)
En primeiro lugar centrámonos na estimación puntual.
Se as medias mostrais son $\overline{X}$ e $\overline{Y}$ respectivamente, entón está claro que un estimador para a diferencia das medias é $\widehat{\mu_1-\mu_2}=\overline{X}-\overline{Y}$.
Para o resto de consideracións desta sección temos varios casos.
Varianzas poboacionais coñecidas
Se $\sigma_1$ e $\sigma_2$ son coñecidas, cousa que habitualmente non sucede, entón o estatístico \[ \frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\sim Z, \] ten unha distribución normal estándar.
Coñecido tal estatístico podemos tanto calcular intervalos de confianza (seguindo o mesmo procedemento estudado no capítulo dedicado a intervalos de confianza), como facer contrastes de hipótese (seguindo o procedemento do capítulo dedicado a contrastes de hipóteses).
Intervalos de confianza
Por exemplo, un intervalo de confianza de nivel de significación $\alpha$ para a diferencia de medias vén determinado pola expresión \[ \Biggl\lvert\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\Biggr\rvert\leq Z_{\alpha/2}. \]
Por tanto, tal intervalo é da forma \[ \biggl[(\overline{X}-\overline{Y}) -Z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}},\, (\overline{X}-\overline{Y}) +Z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\,\biggr]. \] ou ben, \[ (\overline{X}-\overline{Y})\pm Z_{\alpha/2}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}. \]
Contraste de hipóteses
Para un contraste bilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}=(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}\neq(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(-\infty,\,-Z_{\alpha/2})\cup(Z_{\alpha/2},\,+\infty)$.
- Rexión de aceptación: $[-Z_{\alpha/2},\,Z_{\alpha/2}]$.
Para un contraste unilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}\leq(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}>(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(Z_{\alpha},\,+\infty)$.
- Rexión de aceptación: $(-\infty,\,Z_{\alpha}]$.
Para un contraste unilateral esquerdo procederíase de xeito análogo.
Varianzas poboacionais descoñecidas pero iguais
Supoñamos agora que $\sigma^2=\sigma_1^2=\sigma_2^2$ é a varianza (coincidente) das dúas poboacións. Non obstante, $\sigma$ é descoñecida.
En primeiro lugar temos que estima-la varianza. Para iso temos dous estimadores da mesma cantidade, $s_1^2:=s_{X,\,n_1-1}^2$ e $s_2^2:=s_{Y,\,n_2-1}^2$, obtidos a partir das dúas mostras. Para uni-la información obtida por ambos, calculámo-la cuasi-varianza mostral conxunta.
A cuasi-varianza mostral conxunta defínese como \[ s_p^2=\frac{(n_1-1)s_{1}^2+(n_2-1)s_{2}^2}{n_1+n_2-2}, \] que é a media ponderada das cuasi-varianzas das mostras.
Agora podemos considera-lo estatístico para resolve-los problemas.
O estatístico \[ \frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t_{n_1+n_2-2}, \] ten unha distribución $t$-Student con $n_1+n_2-2$ graos de liberdade.
Para determinar se podemos considera-la varianzas de dúas poboacións iguais ou non, unha posibilidade é empregar un test de hipóteses sobre a varianza, tal e como se describe na sección dedicada á comparación das varianzas de dúas poboacións con mostras independentes.
Outra posibilidade empregada habitualmente consiste en aceptar que $\sigma_1=\sigma_2$ cando se ten \[ \frac{1}{2}\leq \frac{s_1^2}{s_2^2}\leq 2, \] é dicir, cando ningunha das cuasi-varianzas é máis do doble da outra.
Intervalos de confianza
Agora un intervalo de confianza de nivel de significación $\alpha$ para a diferencia de medias vén determinado pola expresión \[ \Biggl\lvert\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\Biggr\rvert\leq t_{n_1+n_2-2,\,\alpha/2}. \]
Por tanto, tal intervalo é da forma (omitímo-los graos de liberdade) \[ \biggl[(\overline{X}-\overline{Y}) -t_{\alpha/2}\,s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}, \,(\overline{X}-\overline{Y}) +t_{\alpha/2}\,s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}\,\biggr], \] ou ben, \[ (\overline{X}-\overline{Y}) \pm t_{\alpha/2}\,s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}. \]
Contraste de hipóteses
Para un contraste bilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}=(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}\neq(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(-\infty,\,-t_{\alpha/2})\cup(t_{\alpha/2},\,+\infty)$.
- Rexión de aceptación: $[-t_{\alpha/2},\,t_{\alpha/2}]$.
Para un contraste unilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}\leq(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}>(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(t_{\alpha},\,+\infty)$.
- Rexión de aceptación: $(-\infty,\,t_{\alpha}]$.
En lugar de fixar un nivel de significación poderiamos ter calculado o valor $P$.
Para un contraste unilateral esquerdo procederíase de xeito análogo.
Descoñecidas as varianzas poboacionais
Se $\sigma_1^2$ e $\sigma_2^2$ son descoñecidas e non poden ser supostas iguais, entón non hai solución exacta para o problema de determina-la distribución na mostraxe de $\overline{X}-\overline{Y}$, o cal obriga a adoptar solucións aproximadas.
Cando os tamaños das mostraxes son grandes, cabe argumentar que $s_{1}^2$ e $s_{2}^2$ son boas aproximacións de $\sigma_1^2$ e $\sigma_2^2$. Así, \[ \frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}, \] terá unha distribución aproximadamente normal.
Non obstante, neste curso empregarémo-lo feito de que o estatístico anterior está mellor aproximado por unha $t$-Student cuns certos graos de liberdade.
A aproximación debida a Welch-Smith-Satterthwaite define a cantidade $\gamma$ de graos de liberdade, como \[ \gamma\sim\frac{\Bigl(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\Bigr)^2} {\frac{\bigl(s_1^2/n_1\bigr)^2}{n_1-1}+\frac{\bigl(s_2^2/n_2\bigr)^2}{n_2-1}}. \] Como $\gamma$ ten que ser enteiro, tomarase como valor a parte enteira do valor obtido no cálculo.
Así, o estatístico que empregaremos \[ \frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}, \] terá, aproximadamente, unha distribución $t$ de Student con $\gamma$ graos de liberdade, onde $\gamma$ está definido mediante a fórmula de Welch.
Intervalos de confianza
No caso máis xeral, un intervalo de confianza de nivel de significación $\alpha$ para a diferencia de medias vén determinado pola expresión \[ \Biggl\lvert\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)} {\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\Biggr\rvert\leq t_{\gamma,\,\alpha/2}. \]
Por tanto, tal intervalo é da forma \[ \biggl[(\overline{X}-\overline{Y}) -t_{\gamma,\,\alpha/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}, \,(\overline{X}-\overline{Y}) +t_{\gamma,\,\alpha/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}} \,\biggr], \] ou ben, \[ (\overline{X}-\overline{Y}) \pm t_{\gamma,\,\alpha/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}. \]
Contraste de hipóteses
Para un contraste bilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}=(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}\neq(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(-\infty,\,-t_{\gamma,\,\alpha/2}) \cup(t_{\gamma,\,\alpha/2},\,+\infty)$.
- Rexión de aceptación: $[-t_{\gamma,\,\alpha/2},\,t_{\gamma,\,\alpha/2}]$.
Para un contraste unilateral \[ \begin{aligned} H_0\colon \mu_1-\mu_2 &{}\leq(\mu_1-\mu_2)_0,& H_1\colon \mu_1-\mu_2 &{}>(\mu_1-\mu_2)_0, \end{aligned} \] con nivel de significación $\alpha$, temos:
- Rexión crítica: $(t_{\gamma,\,\alpha},\,+\infty)$.
- Rexión de aceptación: $(-\infty,\,t_{\gamma,\,\alpha}]$.
En troques de fixar un nivel de significación poderiamos ter calculado o valor $P$ como \[ P=P(t_{\gamma}\geq\text{valor no estatístico}), \] e decidir, se tal valor é moi pequeno, que rexeitámo-la hipótese nula; de non ser así, aceptámola.
Para un contraste unilateral esquerdo procederíase de xeito análogo.
Un isótopo radioactivo (Sr-90) acumúlase nos ósos por medio do leite de vaca consumido. Quérese coñecer se o nivel de isótopo nos nenos é distinto ca nos adultos. Para iso tómase:
- unha mostra aleatoria de 121 nenos; obtense unha concentración media de 2.6 picocurios/g, cunha cuasi-desviación típica de 1.2.
- outra mostra de 61 adultos; para estes tense como media 0.4 e cuasi-desviación típica 0.11.
Denotemos por $X$ á variable aleatoria que mide o nivel de isótopo nos nenos, e por $Y$ á dos adultos. Asumímo-las notacións que vimos empregando nesta sección. Trátase pois dun problema de contraste de hipóteses bilateral, é dicir, \[ \begin{aligned} H_0\colon \mu_1&{}=\mu_2,& H_1\colon \mu_1&{}\neq\mu_2. \end{aligned} \] Equivalentemente, miramos se a diferencia $\mu_1-\mu_2$ é nula.
O problema dános como datos: $n_1=121$, $\overline{X}=2.6$, $s_1=1.2$, $n_2=61$, $\overline{Y}=0.4$, $s_2=0.11$.
Xa que non hai coñecemento das varianzas, e $s_1^2/s_2^2=1.2^2/0.11^2=119.008> 2$, empregámo-la fórmula de Welch, co que substituíndo: \[ \gamma\sim\frac{\Bigl(\frac{1.2^2}{121}+\frac{0.11^2}{61}\Bigr)^2} {\frac{\bigl(1.2^2/121\bigr)^2}{120}+\frac{\bigl(0.11^2/61\bigr)^2}{60}} =123.965, \] Así que tomamos $\gamma=123$. Realmente a distribución $t_{123}$ é moi parecida á normal estándar.
Substituíndo no estatístico obtemos: \[ \frac{(2.6-0.4)-0}{\sqrt{\frac{1.2^2}{121}+\frac{0.11^2}{61}}}=20.001. \] Este valor está fóra de intervalos da forma $[-t_{123,\,\alpha/2},\,t_{123,\,\alpha/2}]$ para valores moito menores a $\alpha=0.1\%$. (Por exemplo, $t_{123,\,0.0005}=3.371$.) O cálculo do valor $P$ con software informático daría (nótese que é un contraste bilateral cun estatístico simétrico) $P=2P(t_{123}>20.001)=0.2\cdot 10^{-39}$, que é un valor moi pequeno.
Conclusión: rexeitámo-la hipótese nula e concluímos que hai evidencia significativa, cunha confianza de máis do 99.9%, de que o nivel de isótopo en nenos é distinto ó dos adultos.
En vista dos resultados obtidos no problema anterior, preguntámonos agora se hai evidencia significativa de que a media obtida para os nenos sexa maior cá dos adultos. ¿É maior ca 2 picocurios/g?
As variables aleatorias a considerar son as mesmas cá no problema anterior.
Como necesitamos evidencia concluínte de que a dos nenos é significativamente maior, temos que estuda-lo contraste: \[ \begin{aligned} H_0\colon \mu_1&{}\leq\mu_2,& H_1\colon \mu_1&{}>\mu_2. \end{aligned} \]
Neste caso calculámo-lo valor $P$ substituíndo no estatístico: \[ \begin{aligned} P&{}=P\biggl(t_{123}\geq \frac{(2.6-0.4)-0}{\sqrt{\frac{1.2^2}{121}+\frac{0.4^2}{61}}}\biggr)\\ &{}=P(t_{123}\geq 20.001)=0.9\cdot 10^{-40}. \end{aligned} \]
Conclusión: rexeitámo-la hipótese nula e concluímos que hai evidencia significativa, cun nivel de confianza moi alto, de que o nivel de isótopo en nenos é superior ó dos adultos.
A última pregunta correspóndese a un contraste de hipóteses \[ \begin{aligned} H_0\colon \mu_1-\mu_2&{}\leq 2,& H_1\colon \mu_1-\mu_2&{}>2. \end{aligned} \]
Procédese igual, pero agora o valor no estatístico é \[ \frac{(2.6-0.4)-2}{\sqrt{\frac{1.2^2}{121}+\frac{0.11^2}{61}}}=1.818, \] co cal, o valor $P$ é $P=P(t_{123}\geq 1.818)=0.0357$.
Agora $0.025<P<0.05$, así que parece que podemos rexeita-la hipótese nula con nivel de confianza do 95%, pero non do 97.5%.
Conclusión: rexeitámo-la hipótese nula e por tanto concluímos que hai evidencia significativa, polo menos ó 95%, de que a diferencia de concentración de isótopo Sr-90 en nenos é superior a 2 picocurios/g con respecto á dos adultos.
Comparación das varianzas de dúas poboacións con mostras independentes
Na sección anterior vimos que é máis sinxelo, e que non hai que facer aproximacións, para estima-la diferencia de medias se supoñemos que as varianzas poboacionais son iguais. A utilidade desta sección é precisamente dar un test de hipóteses para contrastar se as varianzas poboacionais son iguais.
De novo suporemos que $X$ e $Y$ seguen distribucións normais, $N(\mu_1,\sigma_1)$ e $N(\mu_2,\sigma_2)$, respectivamente. Extraemos dúas mostras independentes de cada poboación, $X_1,\dots,X_{n_1}$ e $Y_1,\dots,Y_{n_2}$.
Como anteriormente, denotamos por $s_1^2$ e $s_2^2$ as cuasi-varianzas das mostras anteriores. Para comparar $\sigma_1^2$ e $\sigma_2^2$, non é conveniente considera-lo estatístico $s_1^2-s_2^2$. Por varias razóns é preferible emprega-lo cociente.
Para compara-las varianzas de dúas poboacións normais a partir de mostras independentes emprégase o estatístico \[ \frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}\sim F_{n_1-1,\,n_2-1}, \] que segue unha distribución $F$ de Fisher-Snedecor con $(n_1-1,\, n_2-1)$ graos de liberdade.
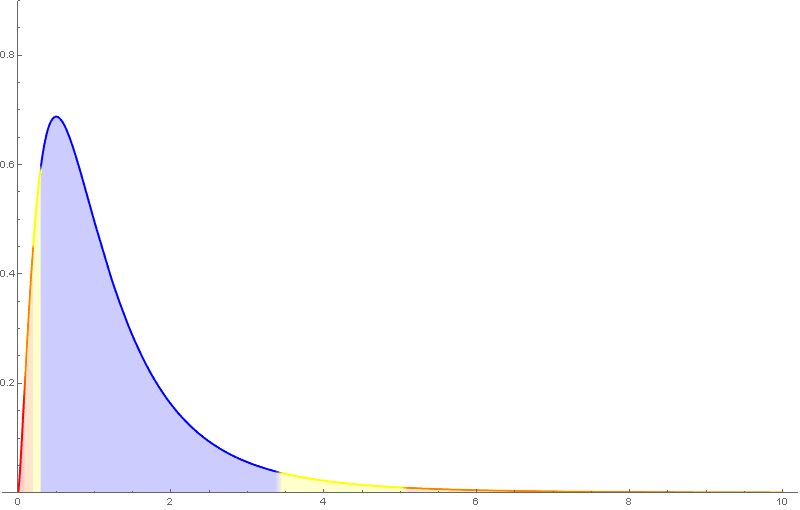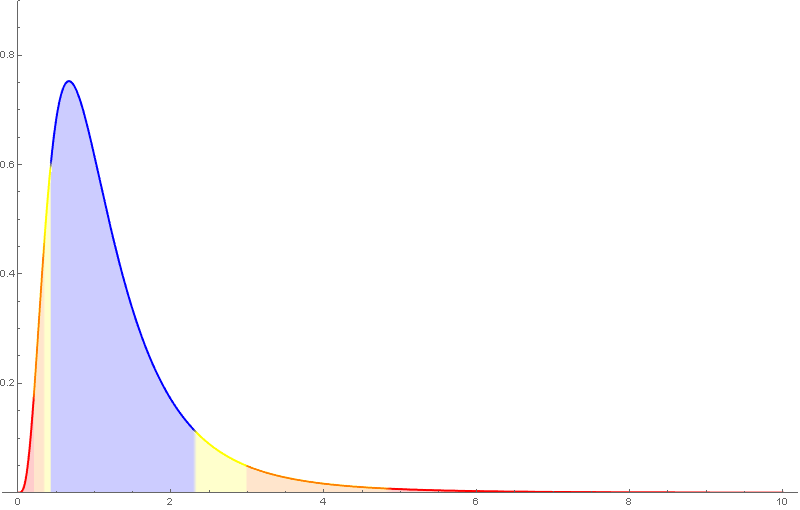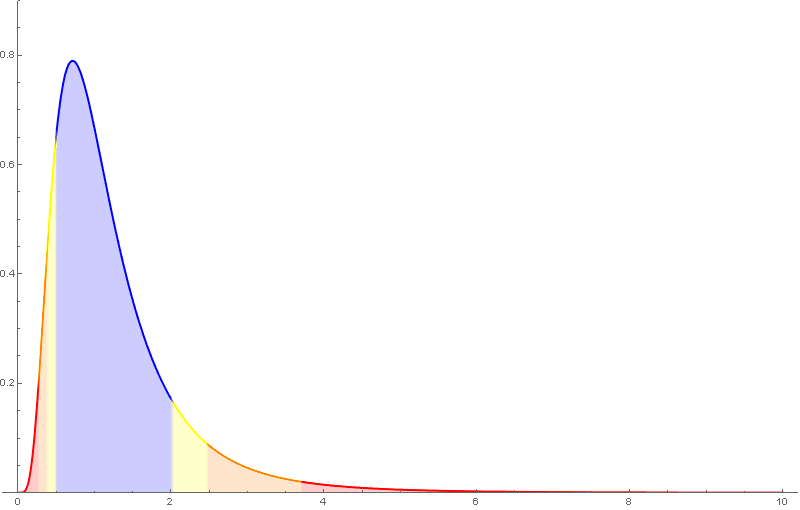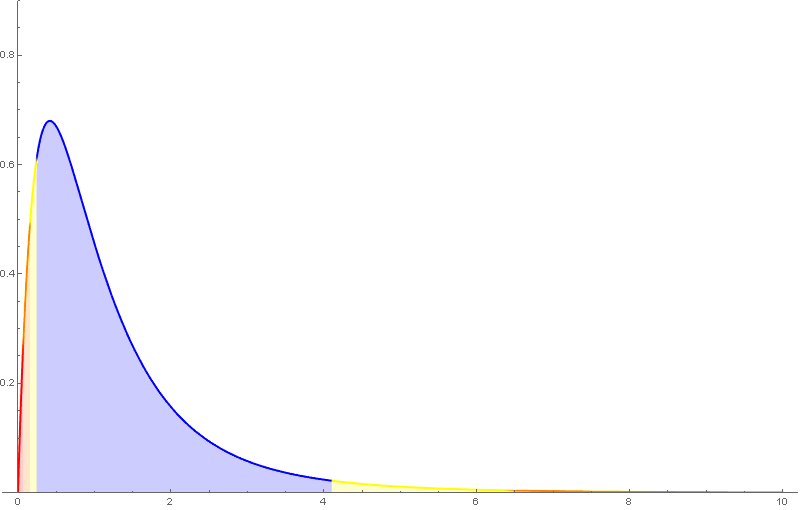
A distribución de probabilidade da $F_{m,n}$ ten como función de densidade unha función da forma \[ f(x)=c_{m,n}\,x^{\frac{m}{2}-1}(n+mx)^{-\frac{m+n}{2}},\quad x>0, \] sendo $c_{m,n}$ unha determinada constante.
A distribución $F$ de Snedecor depende de dous parámetros, tamén chamados graos de liberdade, que haberá que considerar á hora de buscar valores nas táboas.
Algunhas propiedades da $F$ de Snedecor:
- $E(F_{m,n})=\frac{n}{n-2}$ se $n>2$.
- Só está definida para valores positivos e non é simétrica.
- Se $F_{m,\,n,\,\alpha}$ é o valor para o que $P(F_{m,\,n}>F_{m,\,n,\,\alpha})=\alpha$, entón \[ F_{n,\,m,\,\alpha}=\frac{1}{F_{m,\,n,\,1-\alpha}}. \]
Nótese que nas táboas da $F$ de Snedecor empregadas neste curso, o primeiro índice é o das columnas.
Contraste de hipóteses
Estamos interesados no contraste de hipóteses \[ \begin{aligned} H_0\colon \sigma_1^2 &{}=\sigma_2^2,& H_1\colon \sigma_1^2 &{}\neq\sigma_2^2. \end{aligned} \]
Como por hipótese, $\sigma_1^2=\sigma_2^2$, o estatístico anterior simplifícase e temos que empregar $s_1^2/s_2^2$ que, como vimos, ten distribución $F_{n_1-1,\,n_2-1}$. En consecuencia, para un nivel de significación $\alpha$ temos:
- Rexión crítica: $\bigl(0,\,\frac{1}{F_{n_2-1,\,n_1-1,\,\alpha/2}}\bigr)\cup \bigl(F_{n_1-1,\,n_2-1,\,\alpha/2},\,+\infty\bigr)$.
- Rexión de aceptación: $\bigl[\frac{1}{F_{n_2-1,\,n_1-1,\,\alpha/2}},\,F_{n_1-1,\,n_2-1,\,\alpha/2}\bigr]$.
Realizouse un estudo sobre as necesidades enerxéticas para o crecemento e mantemento dun niño de avións en Perthshire, Escocia. Obtivéronse os seguintes resultados para as observacións de dúas mostras independentes da variable normal "número de kilocalorías por gramo e hora que se requiren por paxaro".
| Adultos incubando | Adultos precriando |
|---|---|
| $n_1=57$ | $n_2=12$ |
| $\overline{X}=0.0167$ | $\overline{Y}=0.0144$ |
| $s_1=0.0042$ | $s_2=0.0024$ |
¿Indican estes datos que o número de kilocalorías requerido por adultos que están incubando é maior có requerido polos adultos que están precriando? Razoalo empregando o valor P. (Facer un contraste de hipóteses para determina-la igualdade das varianzas empregando para iso $\alpha=0.1$.)
Sexa $X$ a variable aleatoria que mide o número de kilocalorías por gramo e hora que se requiren por paxaro en adultos incubando, e $Y$ a que mide o mesmo valor en adultos precriando.
Trátase dun problema de contraste de hipóteses da media de dúas poboacións, que coa notación que vimos empregando, se escribe como \[ \begin{aligned} H_0\colon \mu_1&{}\leq \mu_2,& H_1\colon \mu_1&{}>\mu_2. \end{aligned} \]
En primeiro lugar teremos que decidir se podemos supoñer que as varianzas poboacionais son ou non iguais. Isto require un contraste de hipóteses previo: \[ \begin{aligned} H_0\colon \sigma_1^2&{}= \sigma_2^2,& H_1\colon \sigma_2^2&{}\neq\sigma_2^2. \end{aligned} \]
Substituíndo no estatístico $s_1^2/s_2^2$ obtemos $0.0042^2/0.0024^2=3.0625$. Por outro lado, para $\alpha=0.1$ temos $F_{56,11,0.05}=2.4960$ e $F_{56,11,0.95}=0.5091$. Claramente $3.0625\notin[0.5091,2.4960]$, co que debemos rexeita-la última hipótese, e por tanto non podemos supoñer que $\sigma_1$ e $\sigma_2$ sexan iguais.
Temos que empregar entón a aproximación de Welch. Primeiro calculámo-los graos de liberdade: \[ \frac{\Bigl(\frac{0.0042^2}{57}+\frac{0.0024^2}{12}\Bigr)^2} {\frac{(0.0042^2/57)^2}{57-1}+\frac{(0.0024^2/12)^2}{12-1}} =27.51, \] así que tomamos $\gamma=27$.
Substituímos agora no estatístico: \[ \frac{(0.0167-0.0144)-0}{\sqrt{\frac{0.0042^2}{57}+\frac{0.0024^2}{12}}}=2.589. \]
Entón o valor $P$ é $P=P(t_{27}\geq 2.589)=0.0077$, é dicir, $0.005<P<0.01$.
Conclusión: rexeitámo-la hipótese nula e concluímos que existe evidencia significativa, polo menos do 99%, de que o número de kilocalorías requerido por adultos incubando é maior có requerido polos adultos que están precriando.
Nun estudo sobre hábitos de alimentación de morcegos, márcanse 25 femias e 11 machos e rastréanse por radio. A variable de interese é "distancia que percorren voando en busca de alimento". O experimento proporciona a seguinte información:
| Femias | Machos |
|---|---|
| $n_1=25$ | $n_2=11$ |
| $\overline{X}=205$ | $\overline{Y}=135$ |
| $s_1=100$ | $s_2=95$ |
Calcular un intervalo de confianza para a diferencia de medias cun nivel de confianza do 90%.
Sexa $X$ a variable aleatoria que mide a distancia que percorre un morcego femia voando en busca de alimento, e $Y$ a que mide a mesma distancia para morcegos macho.
Para calcula-lo intervalo de confianza pedido, primeiro temos que decidir que estatístico empregamos. Por tanto, hai que determinar se podemos supoñer que as varianzas poboacionais poden ser consideradas iguais ou non.
Así, investigámo-lo contraste de hipóteses \[ \begin{aligned} H_0\colon \sigma_1^2&{}= \sigma_2^2,& H_1\colon \sigma_2^2&{}\neq\sigma_2^2. \end{aligned} \]
Subsituíndo no estatístico $s_1^2/s_2^2$ obtemos $100^2/95^2=1.108$. Por outro lado, para $\alpha=0.1$, $F_{24,10,0.05}=2.737$ e $F_{24,10,0.95}=0.4435$. Dado que o valor no estatístico cae entre os dous, aceptamos que as dúas varianzas poboacionais son iguais.
Podemos, por tanto, toma-la varianza conxunta \[ s_p^2=\frac{(15-1)\cdot 100^2+(11-1)\cdot 95^2}{25+11-2}=9713.24. \]
Dado que $t_{34,0.05}=1.691$ o intervalo de confianza buscado é \[ (205-135)\pm 1.691\sqrt{9713.24}\sqrt{\frac{1}{25}+\frac{1}{11}} =70\pm 60.30, \] que despois de face-los cálculos resulta $[9.70, 130.30]$.
Conclusión: cun nivel de confianza do 90%, a diferencia entre a distancia media percorrida por un morcego femia e un morcego macho en busca de comida sitúase entre 9.70 e 130.30 metros.
Fixémonos que os resultados obtidos supoñendo que as varianzas poboacionais son iguais non é moi distinto do que se obtería se empregarámo-lo método xeral. Para o método xeral o número de graos de liberdade estímase por \[ \frac{\Bigl(\frac{100^2}{25}+\frac{95^2}{11}\Bigr)^2} {\frac{(100^2/25)^2}{25-1}+\frac{(95^2/12)^2}{11-1}} =20.13, \] de xeito que tomamos $\gamma=20$.
A continuación calculamos $t_{20,0.05}=1.72472$. Por tanto, o intervalo calcúlase como \[ (205-135)\pm 1.72472\sqrt{\frac{100^2}{25}+\frac{95^2}{11}}, \] e facendo os cálculos resulta $[9.75, 130.25]$, que é moi similar ó obtido anteriormente.
Comparación de proporcións de dúas poboacións con mostras independentes
Supoñamos que hai dúas poboacións, nas que unha determinada propiedade se dá con probabilidades $p_1$ e $p_2$, respectivamente. Tomamos dúas mostras aleatorias simples de cada poboación, $X_1,\dots,X_{n_1}$ da primeira, e $Y_1,\dots,Y_{n_2}$ da segunda.
De novo, o estimador puntual é o esperado:
Para estima-la diferencia de proporcións emprégase a diferencia das proporcións das mostras: $\widehat{p_1-p_2}=\hat{p}_1-\hat{p}_2$.
Tómase o estatístico \[ \frac{(\widehat{p_1-p_2})-(p_1-p_2)} {\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}} \sim Z, \] que ten distribución normal $N(0,1)$.
Intervalos de confianza
Para un nivel de significación $\alpha$, un intervalo de confianza para a diferencia de proporcións vén determinado pola expresión \[ \Biggl\lvert\frac{(\widehat{p_1-p_2})-(p_1-p_2)} {\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}} \Biggr\rvert\leq Z_{\alpha/2}. \]
Por tanto, un intervalo de confianza será da forma: \[ (\widehat{p_1-p_2}) \pm Z_{\alpha/2} \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}. \]
Contraste de hipóteses
Chamamos valor nulo ó valor frente ó que contrastámo-la hipótese (o que en analoxía con outros casos chamariamos $({p}_1-{p}_2)_0$). Dependendo de se este valor é cero ou non, podemos facer unha pequena simplificación. En particular, se o valor nulo é cero, non tomarémo-lo mesmo estatístico que para o cálculo dun intervalo de confianza.
Valor nulo distinto de cero
Para un contraste bilateral \[ \begin{aligned} H_0\colon p_1-p_2 &{}=(p_1-p_2)_0,& H_1\colon p_1-p_2 &{}\neq(p_1-p_2)_0, \end{aligned} \] con $(p_1-p_2)_0\neq 0$, e nivel de significación $\alpha$, temos:
- Rexión crítica: $(-\infty,\,-Z_{\alpha/2})\cup(Z_{\alpha/2},\,+\infty)$.
- Rexión de aceptación: $[-Z_{\alpha/2},\,Z_{\alpha/2}]$.
Para un contraste unilateral \[ \begin{aligned} H_0\colon p_1-p_2 &{}\leq(p_1-p_2)_0,& H_1\colon p_1-p_2 &{}>(p_1-p_2)_0, \end{aligned} \] con $(\hat{p}_1-\hat{p}_2)_0\neq 0$ e nivel de significación $\alpha$, temos:
- Rexión crítica: $(Z_{\alpha},\,+\infty)$.
- Rexión de aceptación: $(-\infty,\,Z_{\alpha}]$.
En troques de fixar un nivel de significación poderiamos calcula-lo valor $P$ como temos feito en exemplos anteriores.
Para un contraste unilateral esquerdo procederíase de xeito análogo.
Valor nulo cero
Nun contraste bilateral escribimos \[ \begin{aligned} H_0\colon p_1-p_2 &{}=0,& H_1\colon p_1-p_2 &{}\neq 0, \end{aligned} \] Como por hipótese as proporcións reais son as mesmas, $\hat{p}_1$ e $\hat{p}_2$ estiman a mesma cantidade. Así, facemos como que as dúas mostras proveñen dunha mesma poboación con proporción descoñecida $p$, e tomámo-la media ponderada das proporcións estimadas en cada mostra.
O estatístico de contraste neste caso simplifícase un pouco e tomamos \[ \frac{\hat{p}_1-\hat{p}_2} {\sqrt{\hat{p}(1-\hat{p})\Bigl(\frac{1}{n_1}+\frac{1}{n_2}\Bigl)}}\sim Z, \] que tamén segue unha distribución normal estándar.
O resto das cuestións son análogas ó caso anterior.
Entre marzo e agosto de 1998 fíxose en Baltimore un ensaio clínico aleatorizado e doble cego para comproba-la eficacia do paracetamol como analxésico para trata-la migraña. Un grupo de voluntarios da zona dividiuse aleatoriamente en dous grupos. A un deles subministróuselle paracetamol e ó outro un placebo. Entre os 147 pacientes que recibiron o paracetamol, 85 notaron disminución de dor ás dúas horas de tomalo, frente a 56 de 142 no caso do grupo de control (o que tomou o placebo). A partir dos resultados deste estudo clínico, ¿hay evidencia suficiente, con nivel de confianza 99%, para afirmar que o paracetamol é un analxésico útil á hora de trata-los síntomas da migraña? ¿É a diferencia de efectividade maior ó 10%?
Sexa $X$ a variable aleatoria que mide a eficacia do paracetamol como analxésico para trata-la migraña, $Y$ a do placebo.
Trátese dun problema de contraste de hipóteses: \[ \begin{aligned} H_0\colon p_1 &{}\leq p_2, & H_1\colon p_1 &{}> p_2, \end{aligned} \] que por tanto ten valor nulo cero.
Témo-los datos: $n_1=147$, $\hat{p}_1=85/147=57.8\%$, $n_2=142$, $\hat{p}_2=56/142=39.4\%$. Así, a media ponderada das proporcións é: \[ \hat{p}=\frac{147\cdot 0.5782 + 142\cdot 0.3944}{147+142}=0.4879. \] Substituíndo no estatístico de contraste: \[ \frac{0.5782 - 0.3944} {\sqrt{0.4879\,(1-0.4879)\Bigl(\frac{1}{147} + \frac{1}{142}\Bigr)}} =3.1262. \]
Por outra banda, o nivel de significación é $\alpha=0.01$. Ademais, $Z_{0.01}=2.3263$. Entón, $3.1262\notin(-\infty,\, 2.3263]$.
Conclusión: rexéitase a hipótese nula, e concluímos que existe evidencia significativa, polo menos do 99%, de que o paracetamol é útil no tratamento da migraña.
Con respecto á segunda pregunta, agora témo-lo contraste de hipóteses \[ \begin{aligned} H_0\colon p_1-p_2 &{}\leq 0.1, & H_1\colon p_1-p_2 &{}> 0.1. \end{aligned} \]
Como o valor nulo non é cero, substituímos no estatístico xeral para obter \[ \frac{(0.5782 - 0.3944) - 0.1} {\sqrt{\frac{0.5782(1-0.5782)}{147} + \frac{0.3944(1-0.3944)}{142}}} =1.4509. \]
O nivel de significación é $\alpha=0.01$. Ademais, $Z_{0.01}=2.3263$. Entón, $1.4509\in(-\infty,\, 2.3263]$.
Conclusión: aceptámo-la hipótese nula e concluímos que non hai evidencia significativa de que a proporción de enfermos de migraña que melloran ás 2 horas de tomar paracetamol supere no 10% ós que tomaron o placebo.
En consecuencia, hai evidencias de que, ante un ataque de migraña, é mellor tomar paracetamol que non tomar nada. Non obstante, a diferencia de proporcións entre enfermos que toman paracetamol e que non toman nada, e melloran ás 2 horas, non supera o 10%.
Determinación do tamaño da mostra
Podemos facer un argumento similar a cando estimámo-lo tamaño da mostra para unha proporción, e así, se facemos $n\leq n_1,n_2$, para un erro máximo $\epsilon$ obtemos (vendo que o máximo de ${x(1-x)}$ está en $x=1/2$) \[ Z_{\alpha/2} \sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}} \leq Z_{\alpha/2} \sqrt{\frac{1}{4n}+\frac{1}{4n}} \leq \epsilon. \] Despexando, $n\geq \frac{Z_{\alpha/2}^2}{2\epsilon^2}$. En consecuencia, teremos que tomar \[ n_1,n_2\geq \frac{Z_{\alpha/2}^2}{2\epsilon^2}. \]
Comparación da media con mostras emparelladas
Nesta sección estudamos un caso que se presenta con bastante frecuencia. É aquel no que as dúas mostras están emparelladas, é dicir, que para cada individuo dunha lle corresponde un da outra, asociado de xeito natural ou a propósito. Isto dáse por exemplo cando se estuda o comportamento de dous xemelgos, nais e fillas, ou o comportamento dunha persoa antes e despois de tomar un medicamento. Nestes casos faise un único sorteo e a segunda mostra dedúcese da primeira.
Os métodos das seccións anteriores non son aplicables xa que, para calcula-los estatísticos correspondentes, facíase uso da independencia entre mostras.
Temos, por tanto, dúas poboacións nas que medimos unha mesma característica, e denotamos por $X$ e $Y$ as variables aleatorias de cada unha. Tomamos $X_1,\dots,X_n$ unha mostra aleatoria simple, que está emparellada con $Y_1,\dots,Y_n$, non independente da anterior, e do mesmo tamaño. Considerámo-la variable aleatoria $D=X-Y$, que supoñemos que está normalmente distribuída. Así, temos unha mostra das diferencias $D_1,\dots,D_n$, onde $D_i=X_i-Y_i$.
En consecuencia, acabamos de reduci-lo problema de dúas mostras a facer inferencia sobre a súa diferencia. No caso da diferencia de medias temos que estudar entón $\mu_D=\mu_1-\mu_2$. Como vimos, o estatístico necesario para estuda-la media é \[ \frac{\overline{D}-\mu_D}{s_D/\sqrt{n}}\sim t_{n-1}, \] que segue unha distribución $t$-Student con $n-1$ graos de liberdade.
O procedemento para obter intervalos de confianza e facer contrastes de hipóteses é, por tanto, o mesmo có discutido para o cálculo de intervalos de confianza para a media, e contraste de hipóteses para a media, respectivamente.
Cabe resaltar que, se ben $\mu_D=\mu_1-\mu_2$ e $\overline{D}=\overline{X}-\overline{Y}$, pola contra $s_D^2\neq s_1^2\pm s_2^2$. En consecuencia, a varianza da diferencia non pode ser deducida das varianzas das dúas variables.
Realízase un estudo para investiga-lo efecto do exercicio no nivel de colesterol no sangue (mg/dl). Tomáronse mostras de sangue nos participantes. Despois someteuse ós individuos a un programa de exercicios, e volvéronse tomar mostras de sangue. Obtivéronse os seguintes datos:
| Persoa | Nivel previo | Nivel posterior |
|---|---|---|
| 1 | 182 | 198 |
| 2 | 232 | 210 |
| 3 | 191 | 194 |
| 4 | 200 | 220 |
| 5 | 148 | 138 |
| 6 | 249 | 220 |
| 7 | 276 | 219 |
| 8 | 213 | 161 |
| 9 | 241 | 210 |
| 10 | 480 | 313 |
| 11 | 262 | 226 |
Construír un intervalo de confianza para a diferencia de medias con nivel de confianza do $90\%$.
En primeiro lugar organizámo-los cálculos para a diferencia, o cadrado das diferencias, e sumámo-los resultados. Denotamos por $X$ á variable aleatoria que mide o nivel de colesterol en sangue antes do exercicio, e $Y$ o nivel despois do exercicio. Tomámo-la diferencia $D=X-Y$.
| Persoa | $X$ | $Y$ | $D$ | $D^2$ | |
|---|---|---|---|---|---|
| 1 | 182 | 198 | -16 | 256 | |
| 2 | 232 | 210 | 22 | 484 | |
| 3 | 191 | 194 | -3 | 9 | |
| 4 | 200 | 220 | -20 | 400 | |
| 5 | 148 | 138 | 10 | 100 | |
| 6 | 249 | 220 | 29 | 841 | |
| 7 | 276 | 219 | 57 | 3249 | |
| 8 | 213 | 161 | 52 | 2704 | |
| 9 | 241 | 210 | 31 | 961 | |
| 10 | 480 | 313 | 167 | 27889 | |
| 11 | 262 | 226 | 36 | 1296 | |
| $\Sigma$ | 2674 | 2309 | 365 | 38189 |
En vista da táboa temos \[ \begin{aligned} \overline{D} &{}=\frac{1}{n}\sum_i D_i=\frac{365}{11}=33.182,\\ s_D^2 &{}=\frac{1}{n-1}\sum_i D_i^2-\frac{n}{n-1}\overline{D}^2 = \frac{38189}{10}-\frac{11}{10}33.182^2 = 2607.76. \end{aligned} \]
Ademais, $t_{10,\,0.05}=1.812$. Así, o intervalo de confianza vén dado por \[ 33.18\pm 1.81\frac{\sqrt{2607.76}}{\sqrt{11}}, \] o que, facendo os cálculos resulta $[5.28,\,61.09]$.
Conclusión: cun nivel de confianza do 90%, a diferencia media de nivel de colesterol entre a xente que fai exercicio e a que non sitúase entre 5.28 e 61.09.
Resumo de contrastes de hipóteses para dúas poboacións
A continuación preséntase unha táboa resumo cos resultados deste capítulo ata agora.