Preliminares

A Estatística é a rama das Matemáticas que estuda e interpreta os procesos aleatorios, para permitir deducir propiedades dunha poboación a partir dun subconxunto pequeno da mesma. Ademais de ter un corpo formal como parte das Matemáticas, a estatística é a miúdo empregada noutras ciencias co obxectivo de permitir establecer correlacións e dependencias entre diversos fenómenos físicos ou naturais.

Estatística descriptiva

A estatística descriptiva é a técnica matemática que organiza e describe un conxunto de datos co propósito de poder entendelos con máis facilidade. A continuación presentamos algúns conceptos relevantes na estatística descriptiva.

Tipos de datos

Os datos poden ter diversa natureza:

• Datos nominais, que son etiquetas para distinguir a uns de outros, como as provincias de nacemento.
• Escalas ordinais, nas que se asigna unha orde, pero na que o número en si non ten relevancia, como a posición dun competidor nunha liga.
• Escalas de intervalo, que son medicións cuantitativas nas que se mide a diferencia entre dúas variables, como a temperatura en graos Celsius.
• Escalas de razón, que son escalas de intervalo cun cero absoluto, como a temperatura en graos Kelvin.

Precisión

A precisión entenderémola como o número de cifras representativas empregadas para expresar unha medida. Aínda que neste curso non faremos especial fincapé neste tema, convén ter en conta que os erros de precisión nos números se van propagando a medida que imos facendo operacións aritméticas. Para certos cálculos (p. ex. o coeficiente de correlación) é necesario empregar unha cantidade suficiente de decimais para non chegar a resultados absurdos.

Medidas de tendencia central

• Moda: valor máis frecuente.
• Mediana: valor $Md$ tal que, unha vez ordeados os datos, divide a estes pola metade.
• Media: é unha medida para datos obtidos como escalas de intervalo ou de razón, e que vén definida do seguinte xeito: \[ \overline{X}=\frac{X_1+\dots +X_n}{n}=\frac{1}{n}\sum_{i=1}^n X_i. \]

Medidas de posición

• Cuartís: análogo á mediana, pero dividindo a distribución en cuartos $Q_1$, $Q_2$ e $Q_3$.
• Percentís: análogo á mediana e ós cuartís, pero dividindo a distribución en cen partes.

Medidas de dispersión

• Rango: diferencia entre o máximo e o mínimo.
• Amplitude intercuartil: diferencia entre $Q_3$ e $Q_1$.
• Desviación mediana: mediana de $\lvert X-Md\rvert$.
• Varianza: \[ s_n^2=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2=\frac{1}{n}\sum_{i=1}^n X_i^2-\overline{X}^2. \]
• Desviación típica: raíz cadrada da varianza.
• Cuasi-varianza: \[ s_{n-1}^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2=\frac{n}{n-1}s_n^2. \]
• Cuasi-desviación típica: raíz cadrada da cuasi-varianza.

Salvo que se especifique o contrario, neste curso asumiremos que $s$ denota a cuasi-desviación típica, e $s^2$ a cuasi-varianza.

Transformación de datos

Se $Y=aX+b$ entón, \[ \begin{aligned} \overline{Y}&{}=a\overline{X}+b,\\ s_{n,Y}^2&{}=a^2 s_{n,X}^2,\\ s_{n,Y}&{}=\lvert a \rvert s_{n,X}. \end{aligned} \]

A miúdo se empregan cambios para modifica-la media e a varianza:

• Puntuacións desviadas: $x=X-\overline{X}$. Así, $\overline{x}=0$ e $s_{n,x}=s_{n,X}$.
• Puntuacións tipificadas: $Z=\frac{1}{s_{n,X}}(X-\overline{X})$. Así $\overline{Z}=0$ e $s_{n,Z}=1$.

Variables aleatorias

Unha variable aletoria pode describirse informalmente como unha variable que mide unha determinada característica numérica dunha poboación, de xeito que os seus valores dependen do resultado dun experimento aleatorio. Ó longo desta sección suporemos que $X$ é unha variable aleatoria absolutamente continua, o que vén a querer dicir que dita variable toma os seus valores nun intervalo.

Toda variable aleatoria ten asociada unha función de distribución que vén dada por $F(x)=P(X\leq x)$, é dicir, $F(x)$ é a probabilidade de que a variable aleatoria $X$ tome un valor menor ou igual ca $x$.

A función de densidade dunha variable aleatoria absolutamente continua é a derivada da súa función de distribución, $f(x)=F'(x)$.

A área baixo a gráfica da función da densidade nun determinado intervalo $[a,b]$ expresa a seguinte probabilidade: \[ P(a\leq X\leq b)=\int_a^b f(x)dx. \] En particular, $P(X\leq b)=F(b)=\int_{-\infty}^b f(x)dx$.

Neste curso calcularanse moitas veces probabilidades do estilo \[ P(X\geq x)=\int_x^\infty f(x)dx. \] Á función $P(X\geq x)=1-F(x)$ tamén se lle chama función de supervivencia da variable aleatoria $X$.

A media ou esperanza de $X$ defínese como \[ E(X)=\int_{-\infty}^{+\infty} xf(x)dx. \] A media ou esperanza da distribución denótase por $\mu$.

A varianza de $X$ defínese como \[ V(X)=\int_{-\infty}^{+\infty} (x-\mu)^2 f(x)dx = E(X^2)-E(X)^2. \] A varianza dunha distribución denótase por $\sigma^2$, e $\sigma$ denotará a súa desviación típica.

O seguinte teorema dá unha idea de como se concentra a probabilidade dunha variable aleatoria arredor da media, sexa cal sexa a súa distribución.

Por exemplo, poñendo $k=2$ na desigualdade de Chebyshev, obtemos $P(\lvert X-\mu\rvert\geq 2\sigma)\leq 1/4$, é dicir, que polo menos tres cuartas partes da probabilidade dunha variable aleatoria arredor da media están contidas entre $(\mu-2\sigma,\mu+2\sigma)$.

Distribución normal

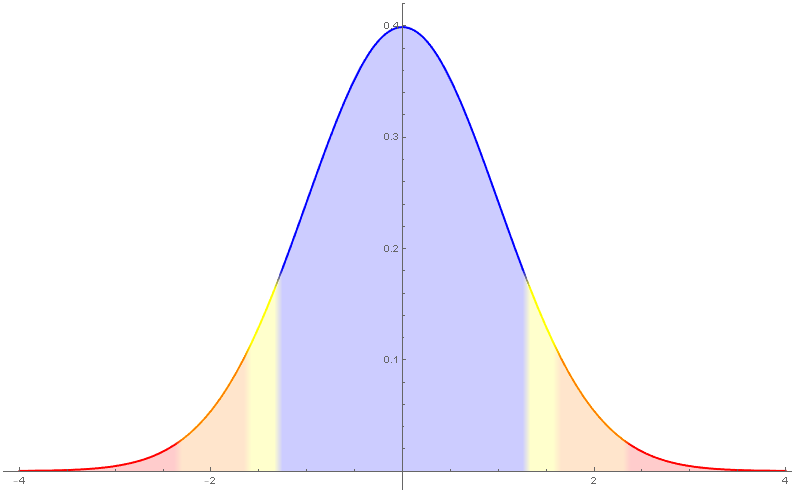
O exemplo máis coñecido e máis útil de variable aleatoria continua vén dado pola distribución normal ou campá de Gauss de media $\mu$ e desviación típica $\sigma$. Denótase por $N(\mu,\sigma)$ e está definida mediante a función de densidade \[ f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}. \]

A función de densidade da distribución normal está definida e é positiva en toda a recta real. Ademais, é simétrica respecto da súa media.

A distribución normal apareceu como un xeito de estima-las desviacións debidas a erros de medida. Tal propiedade está xustificada matematicamente polo teorema central do límite: