Contraste de hipóteses
A finalidade do contraste de hipóteses é decidir se unha determinada hipótese ou afirmación sobre a distribución da poboación pode ser invalidada estatisticamente a partir das observacións contidas nunha mostra.
A hipótese sobre a distribución da poboación denomínase xenericamente hipótese nula e desígnase por $H_0$. Esta pretende contrastarse fronte a unha segunda hipótese chamada hipótese alternativa $H_1$, que agrupa a tódalas posibles poboacións nas que $H_0$ non é certa.
O contraste de hipóteses non ten un comportamento imparcial fronte a $H_0$ e $H_1$, xa que o problema consiste, non en decidir cal das dúas suposicións é máis verosímil en vista dos datos, senón en decidir se a mostra proporciona ou non evidencia suficiente para descartar $H_0$ en favor de $H_1$.
Nun problema de contraste de hipóteses os dous únicos resultados posibles consisten en rexeitar $H_0$ ou non rexeitar (ou aceptar) $H_0$. En xeral, o obxectivo cando se fai un contraste de hipóteses é tratar de rexeitar $H_0$, é dicir, de intentar dar evidencia estatística suficiente para concluír que a hipótese alternativa $H_1$ é certa. Por exemplo, se queremos probar estatisticamente que un determinado medicamento é útil para curar unha enfermidade, a nosa hipótese nula $H_0$ será formular matematicamente que o medicamento non é útil, e a nosa hipótese alternativa, que si que o é. Se conseguimos rexeitar $H_0$ teremos probado estatisticamente que o medicamento é útil. En caso contrario, aceptaremos $H_0$ e concluiremos que non hai evidencia de que o medicamento en cuestión sirva para cura-la enfermidade.
A decisión de rexeitar ou non $H_0$ deberá facerse en vista dos valores obtidos nunha mostra dalgún estatístico que ten unha distribución de probabilidade que, baixo a presunción de que $H_0$ é certa, é coñecido. Este estatístico denomínase estatístico de contraste.
Por tanto, un contraste de hipóteses consiste en dividi-lo espazo mostral en dúas rexións disxuntas. Unha dela chámase rexión crítica ou de rexeitamento, e se a mostra pertence a ela, rexéitase $H_0$ para inclinarse por $H_1$. A outra chámase rexión de aceptación, na que $H_0$ é aceptada en caso de que a mostra pertenza a ela.
Tal e como está presentado o problema existen dúas disxuntivas: a veracidade ou falsedade da hipótese nula, e aceptar ou rexeitar esta. Así, témo-la seguinte casuística:
| $H_0$ é certa | $H_0$ é falsa | |
| rexeitar $H_0$ | erro de tipo I | decisión correcta |
| aceptar $H_0$ | decisión correcta | erro de tipo II |
Para o contraste de hipóteses resulta ás veces interesante facer un símil co sistema xurídico americano. O veredicto dun xurado con respecto a un crime ten dúas posibles decisións: "culpable" ou "non culpable". Nunca se dictamina que alguén é "inocente": a inocencia presuponse (hipótese nula $H_0$) e non é necesario probala. O que si é necesario probar é a culpabilidade (hipótese alternativa $H_1$). Neste sistema intenta minimizase que os inocentes sexan condenados (erro de tipo I), aínda a costa de que haxa culpables que queden impunes (erro de tipo II).
Como en xeral é imposible minimizar simultaneamente os tipos de erro I e II, o criterio tradicional na teoría de contrastes consiste en:
- Fixar un límite para a probabilidade de cometer un erro de tipo I, chamado nivel de significación \[ \alpha=P(\text{rexeitar $H_0$}\mid\text{$H_0$ é certa}). \] A $1-\alpha$ chámaselle nivel de confianza.
- Rexeitar todos aqueles tests que impoñen que a probabilidade de rexeitar $H_0$ cando sexa certa non supere o valor $\alpha$ do nivel de significación.
- Entre tódolos test non excluídos anteriormente, tratar de minimiza-la probabilidade de erro de tipo II. Chámase potencia á probabilidade de detectar que unha hipótese é falsa, \[ \begin{aligned} \beta&{}=P(\text{rexeitar $H_0$}\mid\text{$H_0$ é falsa})\\ &{}=1-P(\text{erro de tipo II}), \end{aligned} \] e por tanto preténdese maximiza-la potencia do método.
Tal procedemento outorga, en principio, prioridade a rebaixa-lo risco de erro de tipo I por debaixo do nivel de significación. De aí que o tratamento que reciben ambas hipóteses sexa asimétrico e estas non sexan intercambiables. De feito, no contraste de hipóteses considérase que $H_0$ é a hipótese establecida, que ten presunción de veracidade, e contra a cal é necesario esgrimir unha grande evidencia para poder invalidala. Así, emprégase un carácter conservador a favor da hipótese $H_0$: o nivel de significación que se fixa intenta garantir que sexa moi infrecuente rexeita-la hipótese correcta. A preocupación por deixar vixente unha hipótese nula falsa (erro de tipo II) é menor, polo que pode aceptarse nese caso un risco máis alto. En consecuencia, se o resultado dun contraste de hipóteses é acepta-la hipótese nula, debe interpretarse que as observacións non aportaron suficiente evidencia para descartala. Pola contra, se se rexeita é porque se está razoablemente seguro de que $H_0$ é falsa e $H_1$ é verdadeira.
O rango de valores $\alpha$ debe estar adaptado á importancia ou trascendencia do problema. A elección do nivel de significación é unha cuestión delicada e importante á que se lle debe prestar atención. Fixémonos cal é a razón de chamarlle a $\alpha$ "nivel de significación". Cando rexeitamos a hipótese nula, é porque obtivemos unha mostra que dá evidencia clara de que esta é falsa. Aínda cabería a posibilidade de que a mostra elixida fose "mala", no sentido de que non representa realmente a poboación. Non obstante, a probabilidade de que iso sucedese é menor ca $\alpha$, e por tanto considérase moi improbable: é dificil que tal mostra aporte eses datos como consecuencia razoable das fluctuacións aleatorias debidas á súa elección. En consecuencia, decídese que a mostra é significativa, e rexéitase a hipótese nula.
Nos problemas estatísticos paramétricos nos que a distribución da poboación pertence a unha familia con parámetros nun conxunto $\Theta$, tanto a hipótese nula como a alternativa serán especificadas mediante subconxuntos disxuntos $\Theta_0$ e $\Theta_1$ tales que $\Theta_0\cup\Theta_1=\Theta$. Deste xeito o contraste de hipóteses escríbese como \[ \begin{aligned} H_0\colon&\, \theta\in\Theta_0,\\[1ex] H_1\colon&\, \theta\in\Theta_1.\\ \end{aligned} \]
Habitualmente os contrastes de hipóteses estudados correspóndense con dúas posibles situacións: os contrastes bilaterais que nós tomaremos da forma $H_0\colon\,\theta=\theta_0$, $H_1\colon\,\theta\neq\theta_0$, e os contrastes unilaterais $H_0\colon\,\theta\leq\theta_0$, $H_1\colon\,\theta>\theta_0$ (ou coas desigualdades invertidas).
Os métodos estatísticos para o deseño de tests de hipóteses son complicados e están fóra dos obxectivos deste curso. Non obstante presentaremos os procedementos para realizar contrastes de hipóteses para poboacións normais nos que se contrastan as características máis habituais.
Contraste de hipóteses para a media da poboación
Supoñamos que temos unha determinada poboación que se rixe por unha distribución de probabilidade normal. Temos unha certa suposición sobre a media e queremos contrasta-la súa veracidade. Para iso tomamos unha mostra aleatoria simple $X_1,\dots,X_n$.
Contrastes bilaterais
Empezamos co caso en que contrastamos un determinado valor da media. Así, \[ \begin{aligned} H_0\colon\mu&{}=\mu_0, &H_1\colon\mu&{}\neq\mu_0. \end{aligned} \]
Supoñendo que $H_0$ fose certa, tomámo-lo estatístico de contraste \[ \frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}\sim t_{n-1} \] que ten, como vimos na sección dedicada ó cálculo de intervalos de confianza para a media con varianza descoñecida, unha distribución $t$-Student con $n-1$ graos de liberdade. (En caso de que a varianza poboacional $\sigma$ fose coñecida tomariámo-lo estatístico $\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim Z$, que ten distribución $Z=N(0,1)$, como consta na sección dedicada ó cálculo de intervalos de confianza para a media con varianza coñecida.)
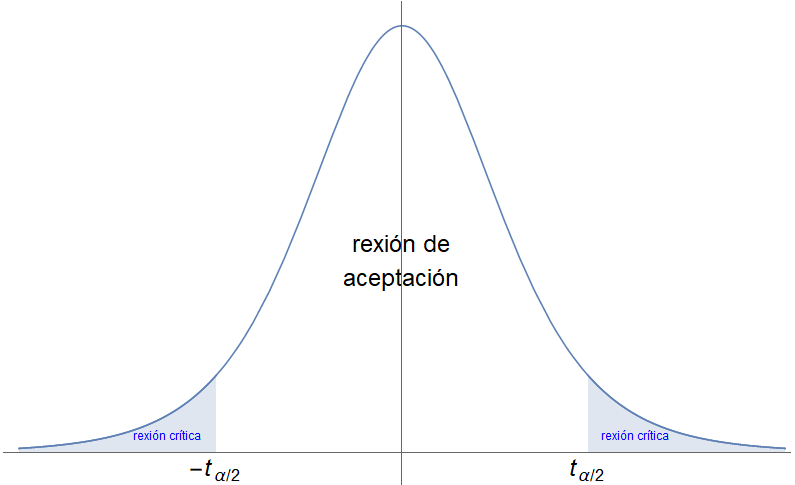
Tomamos un nivel de significación $\alpha$.
- A rexión crítica é $(-\infty,\,-t_{n-1,\,\alpha/2})\cup(t_{n-1,\,\alpha/2},\,+\infty)$, é dicir, cando \[ \left\lvert\frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}\right\rvert> t_{n-1,\,\alpha/2}. \]
- A rexión de aceptación é por tanto $[-t_{n-1,\,\alpha/2},\,t_{n-1,\,\alpha/2}]$.
(En caso de que a varianza sexa coñecida, a rexión crítica é $(-\infty,\,-Z_{\alpha/2})\cup(Z_{\alpha/2},\,+\infty)$, e a rexión de aceptación é $[-Z_{\alpha/2},\,Z_{\alpha/2}]$.)
Cando o valor obtido na mostra está dentro do intervalo de aceptación, aceptamos $H_0$. Cando está na rexión crítica, é dicir, fóra do intervalo de aceptación, rexeitamos $H_0$. Neste caso sempre existe a pequena posibilidade $\alpha$ de que a mostra tomada non sexa representativa da poboación e cometamos un erro de tipo I (rexeitar un modelo correcto); non obstante, a probabilidade disto é pequena, e en vista dos datos deberemos de rexeita-la hipótese nula.
Estudámo-lo crecemento anual dos abetos. Cremos que o valor medio desta variable é $\mu_0=7.25$ Non obstante, nunha mostra de 50 árbores obtívose o valor $\overline{X}=7.27$ e $s_{n-1}=0.03$. ¿É este resultado compatible coa nosa suposición cun nivel de confianza do 95%?
Estudámo-la variable aleatoria $X$="crecemento anual dos abetos".
Neste caso témo-lo contraste de hipóteses \[ \begin{aligned} H_0\colon \mu&{}=7.25, &H_1\colon \mu&{}\neq 7.25. \end{aligned} \]
O nivel de significación é $\alpha=0.05$. Dannos como datos $n=50$, $\overline{X}=7.27$, $s_{n-1}=0.03$.
Xa que a varianza da poboación non é coñecida, empregamos un estatístico $\frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}\sim t_{n-1}$ que ten distribución $t$-Student, e obtemos $t_{49,\,0.025}=2.01$. Como \[ \frac{7.27-7.25}{0.03/\sqrt{50}}=4.71\notin[-2.01,\,2.01], \] o valor obtido está fóra do intervalo de aceptación.
Conclusión: rexeitamos $H_0$ e deducimos que hai evidencia significativa, polo menos do 95%, de que o valor medio de crecemento anual dos abetos non é $\mu_0=7.25$ metros.
Contrastes unilaterais
Neste caso a hipótese nula establece un límite superior ou inferior para a media. Así escribiremos \[ \begin{aligned} H_0\colon\mu&{}\leq\mu_0, &H_1\colon\mu&{}>\mu_0, \end{aligned} \] que é un contraste unilateral dereito, ou ben, \[ \begin{aligned} H_0\colon\mu&{}\geq\mu_0, &H_1\colon\mu&{}<\mu_0, \end{aligned} \] para un contraste unilateral esquerdo.
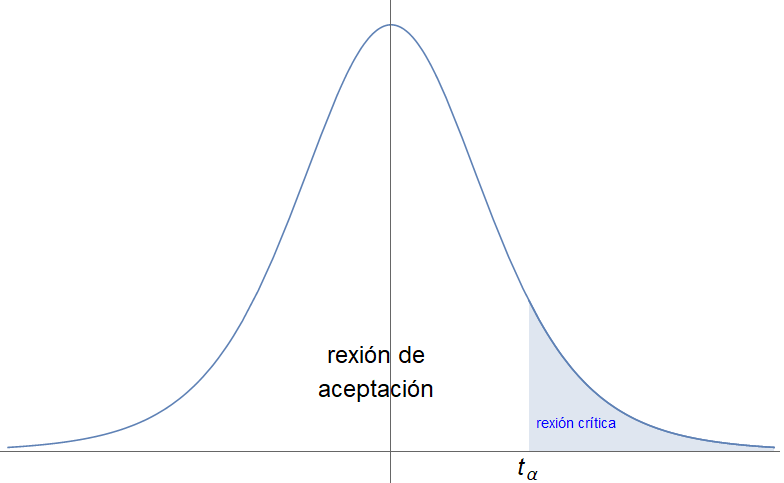
De novo, tomámo-lo estatístico \[ \frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}\sim t_{n-1}, \] que ten, unha distribución $t$-Student con $n-1$ graos de liberdade.
Tomamos un nivel de significación $\alpha$.
- A rexión crítica é $(t_{n-1,\,\alpha},\,+\infty)$ para un contraste unilateral dereito, e $(-\infty,-t_{n-1,\,\alpha})$ para un contraste unilateral esquerdo.
- A rexión de aceptación é por tanto $(-\infty,\,t_{n-1,\,\alpha}]$ para un contraste unilateral dereito, e $[-t_{n-1,\,\alpha},\,+\infty)$ para un contraste unilateral esquerdo.
(En caso de que a varianza poboacional $\sigma$ fose coñecida tomariámo-lo estatístico $\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim Z$, que ten distribución normal $Z=N(0,1)$. A rexión crítica é $(Z_\alpha,\,+\infty)$ para o contraste unilateral dereito, e $(-\infty,\,-Z_\alpha)$ para o contraste unilateral esquerdo. As rexións de aceptación son, respectivamente, $(-\infty,\,Z_{\alpha}]$ e $[-Z_\alpha,\,+\infty)$.)
Igual ca no caso anterior, cando o valor obtido na mostra está dentro do intervalo de aceptación, aceptamos $H_0$. Cando está na rexión crítica, é dicir, fóra do intervalo de aceptación, rexeitamos $H_0$.
A consellería de pesca considera que non se deben extraer ameixas se o número medio de bacterias por centímetro cúbico na auga sobrepasa $70$. Como norma xeral, as rías galegas están por debaixo dese nivel de concentración. Fíxose unha mostraxe en 9 lugares da ría e obtívose un reconto $\overline{X}=71.7$, con $s_{n-1}=2.3$. ¿Que decisión deben toma-los inspectores con nivel de confianza 99%?
Considérase a variable aleatoria $X$="número medio de bacterias por centímetro cúbico na auga".
O contraste de hipóteses a considerar é \[ \begin{aligned} H_0\colon\mu&{}\leq 70, &H_1\colon\mu&{}>70. \end{aligned} \]
O nivel de significación é $\alpha=0.01$, e temos $\mu_0=70$, $n=9$, $\overline{X}=71.7$, $s_{n-1}=2.3$.
Empregámo-lo estatístico $\frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}$, que ten distribución $t$-Student, e obtemos $t_{8,0.01}=2.896$. Como \[ \frac{71.7-70}{2.3/\sqrt{9}}=2.22\in(-\infty,\,2.896], \] o valor obtido está dentro do intervalo de aceptación. Así, este número anormalmente alto non é significativo e probablemente se deba á elección da mostra.
Conclusión: aceptamos $H_0$, o cal quere dicir que non hai evidencia significativa, cun nivel de confianza do 99%, de que o número medio de bacterias por centímetro cúbico de auga sexa maior ca 70. En consecuencia as ameixas son aptas para o consumo.
Para a elección dunha hipótese nula nun contraste unilateral debe considerarse aquela desigualdade para a que se desexe minimiza-la probabilidade de erro de tipo I (rexeitar $H_0$ sendo certa). É dicir, que $H_0$ é a hipótese contra a que hai que esgrimir unha evidencia contundente para rexeitala. Recordemos que nun contraste de hipóteses aquilo que queremos probar debe estar contido na hipótese alternativa.
A normativa cambia e a consellería de pesca require evidencia significativa de que o número medio de bacterias por centímetro cúbico na auga sexa menor ca $70$ para permiti-la extración de ameixas; é fundamental asegurarse de que tal número non é sobrepasado. Coa mostra de 9 lugares da ría obtida de $\overline{X}=71.7$, e $s_{n-1}=2.3$, ¿que decisión deben toma-los inspectores con nivel de confianza 99%? ¿E se fose $\overline{X}=68.7$?
A variable aleatoria considerada segue sendo $X$="número medio de bacterias por centímetro cúbico na auga".
Como agora é importante non sobrepasa-lo valor $70$, e cómpre dar evidencia concluínte diso, o contraste de hipóteses a considerar é \[ \begin{aligned} H_0\colon\mu&{}\geq 70, &H_1\colon\mu&<70. \end{aligned} \]
Igual ca antes, o nivel de significación é $\alpha=0.01$, e temos $\mu_0=70$, $n=9$, $\overline{X}=71.7$, $s_{n-1}=2.3$.
Empregámo-lo estatístico $\frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}$, que ten distribución $t$-Student, e obtemos $t_{8,0.01}=2.896$. Como \[ \frac{71.7-70}{2.3/\sqrt{9}}=2.22\in[-2.896,\,+\infty), \] o valor obtido está dentro do intervalo de aceptación.
Conclusión: aceptamos $H_0$, co que non hai evidencia significativa cunha confianza do 99% de que o número medio de bacterias por centímetro cúbico da auga sexa menor ca 70. Por tanto, hai que prohibi-la extracción de ameixa.
Nota: en realidade resulta superfluo facer un contraste de hipóteses para este caso, xa que a mostra non dá evidencia en contra da hipótese nula (satisfai $\overline{X}\leq \mu_0=70$). Non obstante, vemos que os cálculos claramente confirman esta afirmación.
Para $\overline{X}=68.7$ teriamos \[ \frac{68.7-70}{2.3/\sqrt{9}}=-1.696\in[-2.896,\,+\infty), \] co que aínda neste caso aceptamos $H_0$.
Conclusión: aceptamos $H_0$, co que non hai evidencia significativa cunha confianza do 99% de que o número medio de bacterias por centímetro cúbico da auga sexa menor ca 70. Por tanto, tamén neste caso habería que prohibi-la extracción de ameixa.
Nótese que neste caso é importante que o nivel medio de bacterias sexa menor ca $70$, e por tanto é necesario asegurarse que un valor medio pequeno na mostra non é froito do azar ó escollela.
O valor $P$ ou valor crítico
Intuitivamente o valor $P$ é un número que dá o grao de sorpresa que un experimento causaría nun partidario da hipótese nula.
Para un contraste unilateral dereito correspóndese coa área baixo a curva da función de densidade dunha variable aleatoria $X$ cara á dereita do valor observado polo estatístico de contraste, é dicir, \[ P=P(X\geq\text{valor no estatístico}). \] Para un contraste unilateral esquerdo o valor $P$ é a área baixo a curva da función de densidade cara á esquerda do valor observado polo estatístico de contraste.
Por tanto, cando fagamos un contraste de hipóteses rexeitaremos $H_0$ cando creamos que o valor $P$ é demasiado pequeno para terse producido razoablemente polo azar.
Un estudo dun ecosistema dun bosque de folla caduca indica que o promedio neto de transformacións de nitróxeno en nitrato presenta un incremento de 2Kg por hectárea e ano. Os enxeñeiros de montes cren que unha desfoliación da maleza do bosque conduciría a un descenso dese valor. Arráncase a maleza nun área de 13 hectáreas dun bosque experimental. Límpase a área para impedi-lo crecemento. Despois dun ano determinouse o cambio de nitróxeno a nitrato, por hectárea, analizando a auga da chuvia en 15 puntos dentro do bosque. Obtivéronse os seguintes resultados: $\overline{X}=-3$, $s_{n-1}=7.5$. ¿Proba isto que arranca-la maleza do bosque provoca un descenso no cambio medio neto de nitróxeno a nitrato por hectárea e ano?
A variable aleatoria a considerar é $X$="cambio neto de nitróxeno a nitrato por hectárea e ano".
O contraste a considerar é \[ \begin{aligned} H_0\colon\mu&{}\geq 2, &H_1\colon\mu&{}<2. \end{aligned} \]
Temos como datos $\mu_0=2$, $n=15$, $\overline{X}=-3$, $s_{n-1}=7.5$.
Empregámo-lo estatístico de contraste $\frac{\overline{X}-\mu_0}{s_{n-1}/\sqrt{n}}$, que ten distribución $t$-Student.
Substituíndo, \[ \frac{-3-2}{7.5/\sqrt{15}}=-2.582. \]
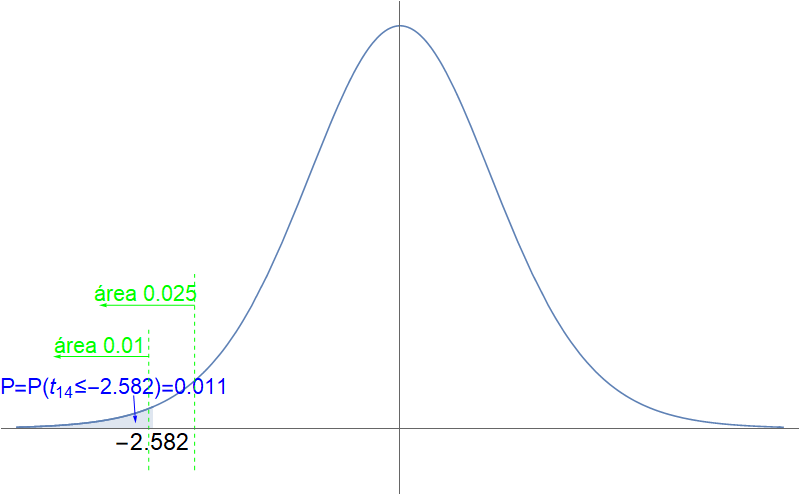
Resulta entón que o $P$-valor é $P=P(t_{14}\leq -2.582)$. Buscando nas táboas (hai que emprega-la simetría da $t$-Student e mira-lo valor á dereita de 2.582) obsérvase que $0.01<P<0.025$. Empregando software informático tense, de feito, $P=0.011$.
Conclusión: como o valor $P$ obtido é pequeno, rexeitamos $H_0$ e concluímos que hai evidencia significativa, polo menos do 97.5%, de que a retirada de maleza do bosque deu como resultado un incremento inferior a 2Kg por hectárea e ano da concentración media de nitróxeno en forma de nitratos.
(Nótese que, se no enunciado do problema nos tivesen pedido un nivel de confianza do 99%, teriamos que ter aceptado a hipótese nula, mentres que se o nivel de confianza fose do 97.5% teriamos que tela rexeitado. Como o valor $P$ se aproxima bastante ó 1%, e cometer un erro de tipo I non parece que vaia ocasionar problemas graves, decidimos que o valor obtido é suficiente para rexeita-la hipótese nula.)
Cómpre enfatizar que como resultado da resolución deste problema, acabamos de probar que o incremento de transformación de nitróxeno en nitrato é menor ca $2Kg$. Non estamos probando que diminúe a transformación de nitróxeno en nitrato (a pesar de que iso é o que pasa na mostra). Se quixeramos probar isto último, teriamos que face-lo contraste de hipóteses \[ \begin{aligned} H_0\colon \mu &{} \geq 0,& H_1\colon \mu &{} < 0. \end{aligned} \] Neste caso, o valor no estatístico resulta \[ \frac{-3 - 0}{7.5 / \sqrt{15}} =-1.549, \] e o valor $P$ é $P=P(t_{14} < -1.549)=0.0718$, que é un valor relativamente grande. Por tanto, para este problema teriamos que aceptar $H_0$, e concluiriamos que non habería evidencia significativa de que a as transformacións medias de nitróxeno en nitrato por hectárea e ano diminuísen.
Cando facemos contrastes bilaterais o procedemento máis común para un estatístico simétrico é considerar un valor $P$ de dúas colas como dúas veces o valor $P$ dunha cola. Non obstante, non existe consenso para calcula-lo valor nestes casos, especialmente se o estatístico non é simétrico.
Contraste de hipóteses para a varianza
Neste caso trátase de facer un contraste de hipótese sobre a varianza dunha poboación normal despois de ter elixido unha mostra aleatoria simple $X_1,\dots,X_n$.
Contrastes bilaterais
O contraste de hipóteses é neste caso \[ \begin{aligned} H_0\colon \sigma^2&{}=\sigma_0^2,& H_1\colon \sigma^2&{}\neq \sigma_0^2. \end{aligned} \]
Suposto que $H_0$ fose certa, tomámo-lo estatístico de contraste \[ \frac{(n-1)s_{n-1}^2}{\sigma_0^2}\sim\chi^2_{n-1}, \] que, como vimos na sección dedicada ó cálculo de intervalos de confianza para a varianza, ten unha distribución $\chi^2$ con $n-1$ graos de liberdade.
Para un nivel de significación $\alpha$ temos:
- Rexión crítica: $[0,\,\chi^2_{1-\alpha/2})\cup(\chi^2_{\alpha/2},\,+\infty)$.
- Rexión de aceptación: $[\chi^2_{1-\alpha/2},\,\chi^2_{\alpha/2}]$.
Se a media é coñecida empregáse o estatítico ${n s_\mu^2}/{\sigma_0^2}$ e procédese de xeito análogo.
Contrastes unilaterais
Supoñemos agora que facemos un contraste unilateral dereito. Tamén suporemos que a media é descoñecida. Se non fose así tomariámo-lo estatístico ${n s_\mu^2}/{\sigma_0^2}$ e procederiamos similarmente. O contraste é entón \[ \begin{aligned} H_0\colon \sigma^2&{}\leq \sigma_0^2,& H_1\colon \sigma^2&{}> \sigma_0^2. \end{aligned} \]
Tomámo-lo mesmo estatístico de contraste ca no caso anterior, co que para un nivel de significación $\alpha$ temos:
- Rexión crítica: $(\chi^2_{n-1,\,\alpha},\,+\infty)$.
- Rexión de aceptación é $[0,\,\chi^2_{n-1,\,\alpha}]$.
Nótese que como esta distribución non é simétrica, para o contraste unilateral esquerdo haberá que tomar:
- Rexión crítica: $[0,\,\chi^2_{n-1,\,1-\alpha})$.
- Rexión de aceptación: $[\chi^2_{n-1,\,1-\alpha},\,+\infty)$.
Ó igual que sucedía co contraste de hipóteses unilateral para a media, unha alternativa para aceptar ou rexeita-la hipótese nula é calcula-lo valor $P$ e comprobar se este número é pequeno ou non.
Contraste de hipóteses para unha proporción
Temos unha poboación na que unha determinada propiedade se dá con probabilidade $p$, tomamos unha mostra aleatoria simple $X_1,\dots,X_n$, e denotamos por $\hat{p}$ á proporción desa propiedade que se dá na mostra.
Contrastes bilaterais
O contraste de hipóteses é neste caso \[ \begin{aligned} H_0\colon p&{}=p_0,& H_1\colon p&{}\neq p_0. \end{aligned} \]
Suposto que $H_0$ fose certa, tomámo-lo estatístico de contraste \[ \frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\sim Z, \] que, como vimos na sección dedicada ó cálculo de intervalos de confianza para a proporción, pode supoñerse que ten unha distribución normal $N(0,1)$ se o tamaño da mostra $n$ é suficientemente grande.
Para un nivel de significación $\alpha$ temos:
- Rexión crítica: $(-\infty,\,-Z_{\alpha/2})\cup(Z_{\alpha/2},\,+\infty)$, é dicir, cando $\Bigl\lvert\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\Bigr\rvert >Z_{\alpha/2}$.
- Rexión de aceptación: $[-Z_{\alpha/2},\,Z_{\alpha/2}]$.
Contrastes unilaterais
Supoñemos agora que facemos un contraste unilateral dereito (para un contraste unilateral esquerdo procederíase de xeito análogo) da forma \[ \begin{aligned} H_0\colon p&{}\leq p_0,& H_1\colon p&{}> p_0. \end{aligned} \]
Tomámo-lo mesmo estatístico de contraste ca no caso anterior, co que para un nivel de significación $\alpha$ temos:
- Rexión crítica: $(Z_\alpha,\,+\infty)$.
- Rexión de aceptación: $(-\infty,\,Z_\alpha]$.
Ó igual ca noutros casos, unha alternativa para aceptar ou rexeita-la hipótese nula é calcula-lo valor $P$ e comprobar se este número é pequeno ou non.
Unha empresa farmacéutica quere comercializar un medicamento que cura certa doenza. Sábese que o 40% dos doentes se curan sen toma-lo medicamento. A empresa debe probar que o seu medicamento é eficaz, e para iso adminístrao a 100 doentes, dos cales se curan 50. ¿É realmente eficaz o medicamento?
A variable aleatoria a estudar é $X$, doentes que se curan despois de tomar certo medicamento.
A cuestión é se o medicamento cura máis ca non tomar nada. Para iso necesitarase evidencia concluínte de que na mostra se obtiveron resultados positivos. Por tanto, o contraste sobre proporcións é \[ \begin{aligned} H_0\colon p&\leq 0.4, &H_1\colon p&{}>0.4. \end{aligned} \]
Temos $p_0=0.4$, $n=100$, e tomámo-lo estatístico de contraste $\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$. Substituíndo os datos: \[ \frac{0.5-0.4}{\sqrt{\frac{0.4(1-0.4)}{100}}}=2.04. \]
O valor $P$ é por tanto $P=P(Z\geq 2.04)=0.0206$. De feito, $0.01<P<0.025$ (xa que 1% e 2.5% son valores máis habituais para niveis de significación). En consecuencia, o resultado é significativo ó 2.5%, pero non ó 1%.
Conclusión: é dubidoso, pero como o nivel crítico é bastante pequeno, poderiamos rexeita-la hipótese nula e aceptar que existe evidencia significativa, polo menos do 97.5%, de que a proporción de curacións entre as persoas que toman o medicamento é maior có 40%.
Unha cuestión que pode ser interesante é ternos preguntado, con anterioridade a ve-los resultados da mostraxe, polo número de casos que satisfán a propiedade buscada para que haxa que rexeita-la hipótese nula.
Poñamos, por exemplo, que témo-lo contraste de hipóteses unilateral esquerdo $H_0\colon p\geq p_0$, $H_1\colon p<p_0$. Supoñamos que o tamaño mostral é $n$, e que o nivel de significación é $\alpha$. Temos que calcula-lo número máximo $k$ de individuos para os que poderiamos rexeita-la hipótese nula $H_0$.
Calculamos en primeiro lugar o valor $Z_\alpha$. Así, para rexeitar $H_0$, necesitamos que o valor no estatístico estea na rexión crítica $(-\infty, -Z_\alpha)$, é dicir, \[ \frac{\frac{k}{n}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}<-Z_\alpha. \] Despexando $k$ na anterior inecuación obtemos \[ k<n\biggl(p_0-Z_\alpha\sqrt{\frac{p_0(1-p_0)}{n}}\biggr). \]
Para analiza-lo risco de sufrir un aborto espontáneo nos embarazos de mulleres hipertensas tratadas con inhibidores de enzima convertidora de angiotensina (IECA) durante o primeiro trimestre do embarazo, estudáronse 329 casos nos que se observaron 47 abortos espontáneos. Se a taxa de abortos espontáneos na poboación fose do 10%,
- ¿Poderíase afirmar que o tratamento con IECA no primeiro trimestre de embarazo incrementa a porcentaxe de abortos espontáneos?
- ¿Cantos casos de abortos espontáneos terían que terse observado na mostra anterior para poder afirmar, cun nivel de significación do 0.05, que a taxa de abortos espontáneos en mulleres hipertensas sometidas a tratamento con IECA no primeiro trimestre de embarazo supera o 20%?
Sexa $X$ a variable aleatoria "abortos espontáneos en mulleres hipertensas sometidas a tratamento con IECA no primeiro trimestre de embarazo".
Para a primeira parte do problema debemos face-lo contraste de proporcións \[ \begin{aligned} H_0\colon p&{}\leq 0.1, &H_1\colon p&{}>0.1. \end{aligned} \]
Os datos do problema dinnos que $p_0=0.1$, $n=329$ e $\hat{p}=47/329=0.143$. Substituíndo no estatístico de contraste obtemos \[ \frac{0.143-0.1}{\sqrt{\frac{0.1(1-0.1)}{329}}}=2.59. \]
O valor $P$ é $P=P(Z\geq 2.59)=0.0048$, que é menor có 0.5%.
Conclusión: rexeitámo-la hipótese nula e concluímos que hai evidencia significativa, polo menos do 99.5%, de que o tratamento con IECA no primeiro trimestre de embarazo provoca que a porcentaxe de abortos espontáneos sexa maior có 10%.
Para a segunda parte do problema témo-lo novo contraste de hipóteses \[ \begin{aligned} H_0\colon p&{}\leq 0.2,& H_1\colon p&{}>0.2. \end{aligned} \] O nivel de significación é $\alpha=0.05$. Así, $Z_\alpha=1.6449$. Por tanto necesitamos atopar $k$ na inecuación \[ \frac{\frac{k}{329}-0.2}{\sqrt{\frac{0.2(1-0.2)}{329}}}>1.6449. \] Despexando obtemos $k>77.73$.
Conclusión: necesitariamos ter rexistrado polo menos 78 casos de abortos espontáneos nunha mostra de 329 mulleres para ter evidencia significativa, polo menos do 95%, de que a taxa de abortos espontáneos en mulleres hipertensas sometidas a tratamento on IECA no primeiro trimestre de embarazo supera o 20%.
Resumo de contrastes de hipóteses para unha poboación
A continuación preséntase unha táboa resumo cos resultados deste capítulo.