Introdución á inferencia estadística. Estimación
Poboación e mostra
A poboación é o conxunto de individuos ou obxectos que queremos estudar.
A nosa hipótese de partida é que a nosa poboación ten unha característica (unha variable aleatoria $X$) que pretendemos estudar (por exemplo, estatura, peso, etc.) que segue unha distribución da que coñécemo-la súa forma xeral (modelo) pero da que descoñécemo-los seus parámetros. Por exemplo, sábese que a estatura segue (aproximadamente) unha distribución normal, pero non coñecemos nin a media nin a desviación típica dunha poboación dada.
Unha mostra aleatoria é un experimento consistente en tomar $n$ individuos da poboación. Suporemos que a mostra aleatoria se consigue extraendo individuos de xeito independente, de modo que tódolos individuos teñan a mesma probabilidade de ser elexidos en cada momento.
Imaxinemos que temos unha bolsa con bólas brancas e negras, e queremos estima-la proporción de bólas brancas. Para iso extraemos unhas cantas bólas, mirámo-la proporción de brancas entre as bólas extraídas, e estimamos que a proporción de bólas brancas totais ten que ser estimada pola proporción de bólas brancas da mostra.
Aínda que efectivamente se pode facer esa estimación, o problema da mostra así extraída é que non é unha mostra aleatoria simple. Os métodos que empregaremos neste curso non contemplan a posibilidade de que a mostra non sexa aleatoria simple. Neste caso, para que a mostra sexa aleatoria simple é necesario face-la extracción con reemprazamento, é dicir, debemos baralla-las bólas, extraer unha, mira-la cor, volvela meter na bolsa, volver a barallar, sacar de novo, e así sucesivamente.
Ademais de que a mostra é aleatoria simple, suporemos que a información que nos dá é veraz. Por tanto, construímos así $n$ variables aleatorias $X_1,\dots,X_n$ independentes e coa mesma distribución de probabilidade cá da poboación.
Cando os datos involucran información delicada ou embarazosa, non podemos confiar en que a información da mostra sexa veraz. Hai técnicas para tratar de suplir eses problemas (por exemplo, aleatoriza-las respostas), pero nese caso xa non se pode supoñer que a mostra siga a mesma distribución cá variable aleatoria da poboación.
Nótese que despois de face-lo experimento teremos uns valores concretos $x_1,\dots,x_n$, pero mentres deseñámo-lo experimento eses resultados son descoñecidos e por iso son tratados como variables aleatorias en vez de como números; en efecto, antes de realiza-lo experimento estamos extraendo un individuo descoñecido da poboación, e por tanto, a característica que lle estudamos ten a mesma distribución cá da poboación. Dise que $n$ é o tamaño mostral, e que $X_1,\dots,X_n$ é unha mostra aleatoria simple.
É imposible, sen empregar teoría da probabilidade, decidir de xeito científico o tamaño mostral. Por iso diremos que este é $n$, e máis adiante intentaremos decidir como se calcula de xeito concreto este valor.
Un estatístico é unha función dunha mostra aleatoria simple que expresa unha determinada característica da mostra. Son exemplos de estatísticos a media, a varianza, a cuasivarianza e outras medidas que definimos con anterioridade.
Un estimador puntual é un estatístico que toma valores no espazo de parámetros. A súa misión será a de aproximar un parámetro. Un estatístico que ten como misión estimar un parámetro $\theta$ denótase $\hat{\theta}$. Por exemplo, se a poboación segue unha distribución normal $N(\mu,\sigma)$, $\hat{\mu}$ será un estimador puntual da media, e $\hat{\sigma}$ un estimador puntual da desviación típica.
$\hat{\mu}$
Poboación
Mostra
Estimador
Existen varios xeitos de escoller estimadores puntuais. Neste curso non enfatizarémo-la súa construcción, pero si que prestaremos atención a estimadores insesgados (aqueles para os que a súa media coincide co valor do parámetro que se pretende estimar) e consistentes (aqueles para os que o erro de medida se aproxima a cero cando o tamaño da mostra tende a infinito).
Cando temos uns datos para unha mostra concreta, un estimador puntual dános unha aproximación do parámetro que pretendemos estimar. O problema dun estimador puntual é que non temos idea de se o valor obtido está preto ou lonxe do valor real. Sería interesante ter unha idea do erro cometido coa estimación e acotar probabilisticamente ese erro. Para iso empréganse os chamados intervalos de confianza.
Chámase intervalo de confianza a un par de estatísticos $T_1$ e $T_2$, entre os cales se estima que estará certo parámetro descoñecido $\theta$ dunha distribución, cunha certa probabilidade de acerto determinada pola condición \[ P\bigl(T_1(X_1,\dots,X_n)\leq \theta\leq T_2(X_1,\dots,X_n)\bigr) \geq 1-\alpha, \] ou ben, \[ P\Bigl(\theta\in\bigl[T_1(X_1,\dots,X_n),\,T_2(X_1,\dots,X_n)\bigr]\Bigr) \geq 1-\alpha, \] onde $X_1,\dots,X_n$ é unha mostra aleatoria simple. A probabilidade de éxito na estimación $1-\alpha$ denomínase nivel de confianza. Nestas circunstancias, $\alpha$ é o erro aleatorio ou nivel de significación.
Na descripción dun intervalo de confianza fálase de que a probabilidade de que un parámetro estea entre dous estatísticos sexa $1-\alpha$. Esta é a formulación correcta do problema e o xeito de construí-lo intervalo a nivel teórico. Para datos concretos dunha mostra, os estatísticos transfórmanse en dous valores entre os que se cre que o parámetro buscado está con confianza $1-\alpha$. Insistimos en que para valores concretos se fala de confianza, non de probabilidade. Se por exemplo $\alpha=0.1$, temos unha confianza do 90% de que o valor real se atope no intervalo calculado, é dicir, que en 90 de cada 100 mostras o intervalo conterá o valor real. Non se pode falar de probabilidade con datos concretos, xa que non hai variables aleatorias e tódolos valores son xa coñecidos.
Estimación da media poboacional
O problema que tratamos de resolver nesta sección é o de estima-la media dunha poboación que sabemos que segue unha distribución normal de media $\mu$ e desviación típica $\sigma$ (que en principio son o que queremos estimar). Para iso extraemos unha mostra aleatoria simple $X_1,\dots,X_n$.
Estimación puntual
Un xeito obvio de estima-la media da poboación é emprega-la media da mostraxe.
A media da mostraxe é o estimador puntual $\hat{\mu}=\overline{X}$, onde \[ \overline{X}=\frac{1}{n}\sum_{i=1}^n X_i. \]
Como $X_1,\dots,X_n$ teñen a mesma distribución $N(\mu,\sigma)$ e son independentes, temos \[ \begin{aligned} E(\overline{X})&{}=\mu, &V(\overline{X})&{}=\frac{\sigma^2}{n}. \end{aligned} \] Debido a estas dúas propiedades, a media mostral é un estimador insesgado e consistente.
Estimación por intervalos: coñecida a varianza poboacional
Supoñamos que a distribución poboacional segue unha distribución normal $N(\mu,\sigma)$ onde a varianza $\sigma^2$ é coñecida.
Se $X_1,\dots,X_n$ é unha mostra aleatoria simple, entón tomámo-lo estatístico \[ \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim Z \] que segue unha distribución normal estándar $Z=N(0,1)$.
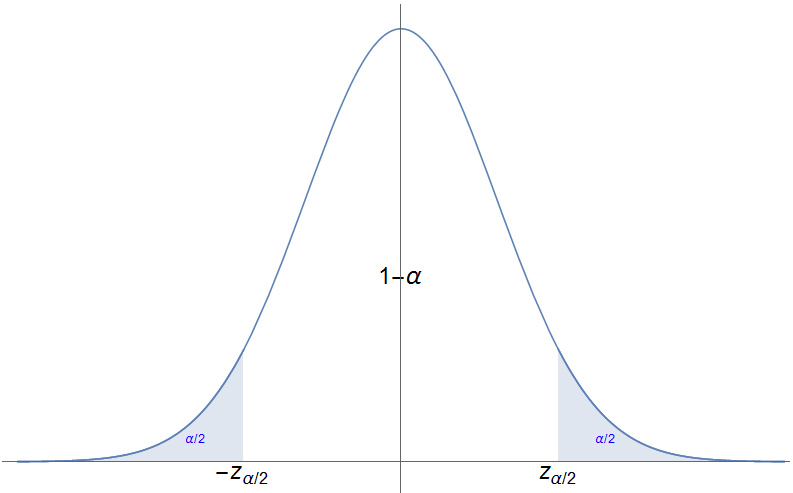
Fixemos agora un nivel de significación $\alpha$ (ou un nivel de confianza $1-\alpha$).
Como a distribución normal é simétrica respecto da media, o noso intervalo de confianza tomarémolo da forma $\bigl[\overline{X}-\epsilon,\overline{X}+\epsilon\bigr]$, onde $\epsilon$ é o erro arredor da media que permitimos cometer. Así pois necesitamos \[ P(\mu\in[\overline{X}-\epsilon,\overline{X}+\epsilon])=1-\alpha. \]
Tomámo-lo valor $Z_{\alpha/2}$ para o que $P(Z\geq Z_{\alpha/2})=\alpha/2$.
Regras para manipular inecuacións
Sexan $x,y$ números. Supoñamos $x\leq y$.
Para calquera $a$,
$x+a\leq y+a$.
Se $a>0$, entón $ax\leq ay$.
Se $a<0$, entón $ax\geq ay$.
Así pois témo-la cadea de igualdades \[ \begin{aligned} 1-\alpha &{}=P\bigl(\lvert\overline{X}-\mu\lvert\leq\epsilon\bigr)\\ &{}=P\Bigl(-\frac{\epsilon}{\sigma/\sqrt{n}}\leq\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \leq\frac{\epsilon}{\sigma/\sqrt{n}}\Bigr)\\ &{}=1-2P\Bigl(Z>\frac{\epsilon}{\sigma/\sqrt{n}}\Bigr), \end{aligned} \] de onde se deduce $Z_{\alpha/2}=\frac{\epsilon}{\sigma/\sqrt{n}}$. Despexando $\epsilon$, témo-lo intervalo de confianza \[ \Bigl[\overline{X}-Z_{\alpha/2}\frac{\sigma}{\sqrt{n}},\, \overline{X}+Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\Bigr]. \]
Equivalentemente, resulta máis sinxelo recordar que a partir do estatístico o intervalo de confianza se obtén despexando $\mu$ da inecuación \[ \left\lvert\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\right\rvert \leq Z_{\alpha/2}, \] ou ben, \[ -Z_{\alpha/2}\leq\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq Z_{\alpha/2}. \]
Outro xeito de escribi-lo intervalo de confianza anterior (aproveitando a simetría do mesmo) é mediante a expresión \[ \overline{X}\pm Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}. \]
Desexamos estima-lo número medio de latexos por minuto para unha certa poboación. Para iso elíxense aleatoriamente 15 individuos e obtéñense os seguintes resultados:
| 78 | 95 | 70 | 97 | 81 |
| 85 | 102 | 75 | 78 | 85 |
| 115 | 80 | 98 | 101 | 92 |
Supoñendo que a distribución da poboación é normal con desviación típica de 10 latexos por minuto, calcula-lo intervalo de confianza do 99% para a media poboacional de número de latexos por minuto.
Considerámo-la variable aleatoria $X$="número de latexos por minuto". Temos que $X$ ten distribución $N(\mu,10)$, con $\mu$ descoñecido.
En primeiro lugar organizámo-los cálculos para calcula-la media mostral.
| $X$ | |
|---|---|
| 78 | |
| 95 | |
| 70 | |
| 97 | |
| 81 | |
| 85 | |
| 102 | |
| 75 | |
| 78 | |
| 85 | |
| 115 | |
| 80 | |
| 98 | |
| 101 | |
| 92 | |
| $\Sigma$ | 1332 |
Tamaño mostral $n=15$. Estimación puntual da media $\overline{X}=1332/15=88.8$ latexos.
Nivel de significación: $\alpha=0.01$. Buscámo-lo valor $Z_{0.005}$ tal que $P(Z\geq Z_{0.005})=0.005$. Aproximadamente, $Z_{0.005}=2.576$.
O intervalo de confianza buscado é entón \[ 88.8\pm 2.576\cdot\frac{10}{\sqrt{15}}=88.8\pm 6.65, \] que resulta ser $[82.1,95.5]$.
Conclusión: cunha confianza do 99%, o número medio de latexos por minuto da poboación estudada atópase entre 82.1 e 95.5.
En ocasións queremos limita-lo erro de estimación para que non sobrepase certo límite. En tal caso hai que tomar unha mostra suficientemente grande. Como o erro vén dado por $Z_{\alpha/2}\,\sigma/\sqrt{n}$, se queremos que sexa menor ca $\epsilon$, entón, despexando, obtemos \[ n\geq\Bigl(\frac{Z_{\alpha/2}\,\sigma}{\epsilon}\Bigr)^2. \]
En caso de que a distribución da poboación non se poida garantir que sexa normal, se o tamaño da mostra é grande, o teorema central do límite dinos que podemos supoñe-la normalidade de $\overline{X}$, e por tanto, os métodos desta sección seguen sendo aproximadamente válidos. Nos apartados seguintes, se a distribución poboacional non é normal, non se aplica o teorema central do límite aínda que o tamaño da mostra sexa grande, así que neses casos habería que empregar outras técnicas que están máis aló dos obxectivos deste curso.
Estimación por intervalos: descoñecida a varianza poboacional
Supoñamos agora que a distribución poboacional segue unha distribución normal $N(\mu,\sigma)$ onde a varianza $\sigma^2$ é descoñecida (o cal é o habitual). Sexa $X_1,\dots,X_n$ é unha mostra aleatoria simple.
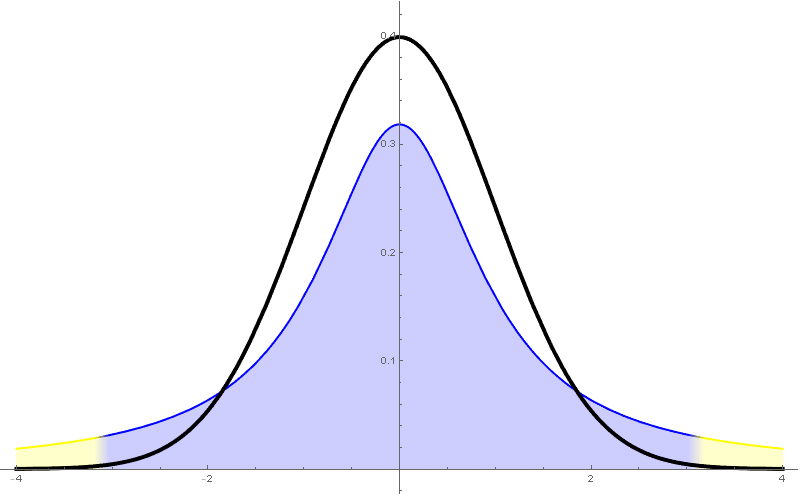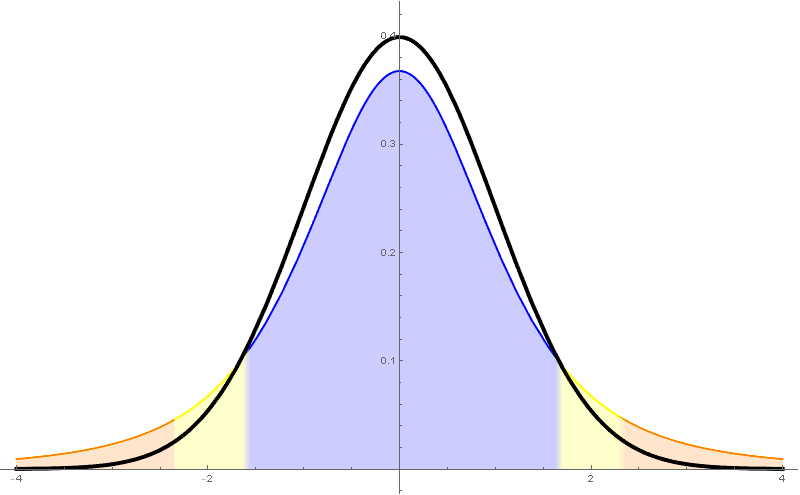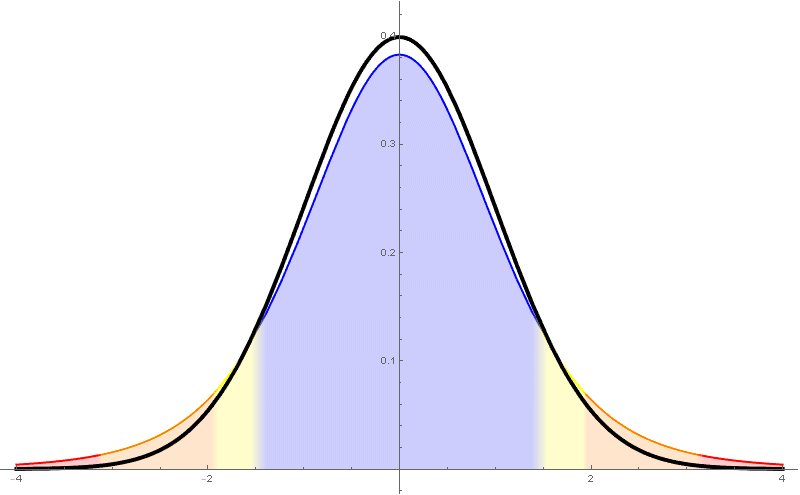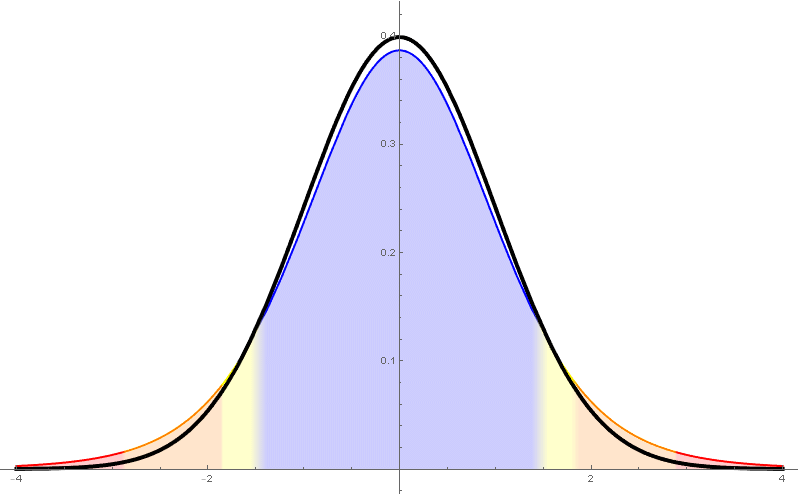
Recordemos que a cuasi-varianza ou varianza mostral (en contraposición a "varianza poboacional") vén definida mediante \[ \begin{aligned} s_{n-1}^2 &{}=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2\\ &{}=\frac{1}{n-1}\sum_{i=1}^n X_i^2-\frac{n}{n-1}\overline{X}^2. \end{aligned} \] Así, a cuasi-desviación típica ou desviación típica mostral, $s_{n-1}$, é a raíz cadrada da cuasi-varianza. Neste curso $s$ denotará, salvo que se diga o contrario, a cuasi-desviación típica $s_{n-1}$.
Para estima-la media cando a varianza poboacional non é coñecida tómase o estatístico \[ \frac{\overline{X}-\mu}{s_{n-1}/\sqrt{n}}\sim t_{n-1}. \] Este estatístico resulta seguir unha distribución $t$-Student de $n-1$ graos de liberdade.

A distribución $t$-Student é unha nova distribución que ten como función de densidade \[ f(x)=c_{n-1}\Bigl(1+\frac{xa^2}{n-1}\Bigr)^\frac{n}{2}, \] sendo $c_{n-1}$ unha constante que non especificaremos.
Nótese que esta distribución depende dun parámetro $n$, chamado graos de liberdade da distribución, e que haberá que ter en consideración cando mirémo-los valores nas táboas.
Algunhas propiedades da $t$-Student:
- $E(t_n)=0$ e $V(t_n)=n/(n-2)$.
- É simétrica respecto da media.
- Ten unha forma parecida á da normal, pero ten cuantiles máis grandes (por tanto produce intervalos de confianza máis grandes).
- Se $n\geq 100$, $t_n$ pode aproximarse por unha $N(0,1)$.
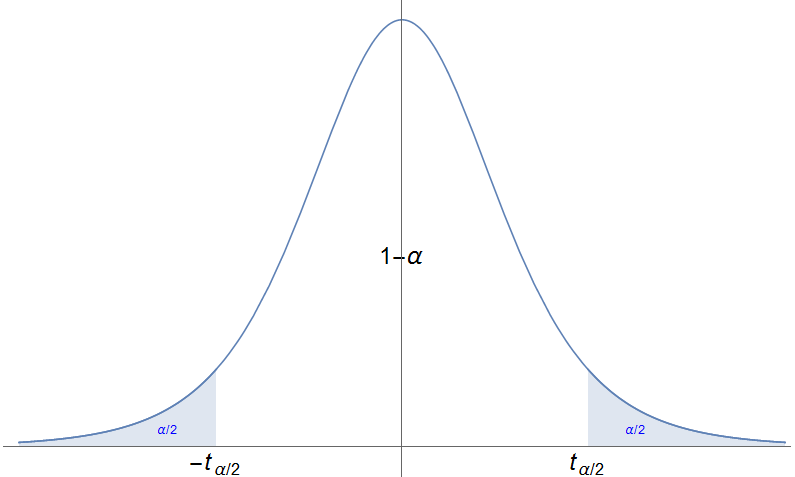
Para o cálculo dun intervalo de confianza, o razoamento sería similar ó do anterior apartado. Para un nivel de significación $\alpha$, o intervalo de confianza para a media vén determinado pola fórmula \[ \Bigl[\overline{X}-t_{n-1,\,\alpha/2}\frac{s_{n-1}}{\sqrt{n}},\, \overline{X}+t_{n-1,\,\alpha/2}\frac{s_{n-1}}{\sqrt{n}}\Bigr], \] ou ben, \[ \overline{X}\pm t_{n-1,\,\alpha/2}\frac{s_{n-1}}{\sqrt{n}}, \] sendo $t_{n-1,\,\alpha/2}$ o valor tal que $P(t_{n-1}\geq t_{n-1,\,\alpha/2})=\alpha/2$.
Igual ca no caso anterior, recordar estas fórmulas non resulta sinxelo. Non obstante, coñecido o estatístico necesario para resolve-lo problema, só temos que lembrar que hai que considera-la inecuación \[ -t_{n-1,\,\alpha/2}\leq\frac{\overline{X}-\mu}{s_{n-1}/\sqrt{n}}\leq t_{n-1,\,\alpha/2}, \] e despexar o valor de $\mu$.
Os pesos ó nacer (en gramos) de 10 nenos, elexidos aleatoriamente nun hospital, son:
| 2750 | 3316 | 3969 | 2211 | 2806 |
| 4195 | 3061 | 3827 | 3572 | 3430 |
Supoñendo que a poboación segue unha distribución normal, calcular un intervalo de confianza do 95% para a media do peso ó nacer dos nenos dese hospital.
Considerámo-la variable aleatoria $X$="peso ó nacer". Temos que $X$ ten distribución $N(\mu,\sigma)$, con $\mu$ e $\sigma$ descoñecidos.
En primeiro lugar, organizámo-los cálculos para a media e cuasi-varianza mostrais.
| $X$ | $X^2$ | |
|---|---|---|
| 2750 | 7562500 | |
| 3316 | 10995856 | |
| 3969 | 15752961 | |
| 2211 | 4888521 | |
| 2806 | 7873636 | |
| 4195 | 17598025 | |
| 3061 | 9369721 | |
| 3827 | 14645929 | |
| 3572 | 12759184 | |
| 3430 | 11764900 | |
| $\Sigma$ | 33137 | 113211233 |
Tamaño mostral $n=10$. Estimación puntual da media $\overline{X}=33137/10=3313.7$. A cuasi-varianza calcúlase como \[ \begin{aligned} s_n^2&{}=\frac{113211233}{10}-3313.7^2=340516,\\ s_{n-1}^2&{}=\frac{10}{9}340516=378351. \end{aligned} \] Extraendo a raíz cadrada obtemos $s_{n-1}=615.10$.
Nivel de significación: $\alpha=0.05$. Buscámo-lo valor $t_{9,0.025}$ tal que $P(t_9>t_{9,0.025})=0.025$. Aproximadamente, $t_{9,0.025}=2.262$.
O intervalo de confianza buscado é entón \[ 3313.7\pm 2.262\cdot\frac{615.10}{\sqrt{10}}=3313.7\pm 440.02, \] ou explicitamente, $[2873.68,3753.72]$.
Conclusión: cunha confianza do 95%, o peso medio ó nacer dos nenos do hospital estudado atópase entre 2873.68 e 3753.72 gramos.
Estimación da varianza poboacional
Nesta sección o problema será o de estima-la varianza dunha poboación que segue unha distribución normal. Tomamos unha mostra aleatoria simple $X_1,\dots,X_n$.
Estimación puntual
Se a media da poboación é coñecida, tomámo-lo seguinte estimador puntual
Definimos \[ s_\mu^2=\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2. \]
Entón, tense \[ E(s_\mu^2)=\sigma^2, \] é dicir, que $s_\mu^2$ é insesgado.
Se a media da poboación é descoñecida, o cal é o que sucede habitualmente, cabería pensar que un estimador para a varianza podería ser $s_n^2=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2$. Isto resulta non se-la mellor idea pois \[ E(s_n^2)=\frac{n-1}{n}\sigma^2, \] é dicir, que este estimador non é insesgado (ten tendencia a infraestima-la varianza.)
Un xeito máis correcto de estima-la varianza da poboación é emprega-la cuasi-varianza.
A cuasi-varianza da mostraxe ou varianza mostral defínese como \[ s_{n-1}^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2. \]
Neste caso, \[ \begin{aligned} E(s_{n-1}^2)&{}=\sigma^2. \end{aligned} \] A cuasi-varianza mostral é un estimador insesgado.
Estimación por intervalos: coñecida a media poboacional
Supoñemos, aínda que normalmente non sucede, que a media poboacional $\mu$ é coñecida. É preferible, por tanto, emprega-lo estimador $s_\mu$ en lugar da cuasi-varianza mostral, xa que o parámetro $\mu$ é coñecido exactamente e non cómpre ser aproximado. En realidade esta é unha situación teórica, pois a media poboacional non é coñecida na práctica, pero serve para ir introducindo unha nova distribución que empregaremos máis adiante.
Para estima-la varianza poboacional dunha poboación normal con media coñecida toma-lo estatístico \[ \frac{n s_\mu^2}{\sigma^2}\sim \chi_n^2, \] que segue unha distribución $\chi$-cadrado de Pearson con $n$ graos de liberdade.
A distribución $\chi^2$ de Pearson ten como función de densidade de probabilidade \[ f(x)=c_n\, x^{n/2-1} e^{-x/2},\ x>0, \] onde $c_n$ é unha constante.
A distribución $\chi^2$ de Pearson, ó igual que sucedía coa distribución $t$ de Student, depende dun parámetro que se coñece como o número de graos de liberdade da distribución.

Algunhas propiedades da $\chi^2$ de Pearson:
- $E(\chi^2_n)=n$ e $V(\chi^2_n)=2n$.
- Só está definida para valores positivos e non é simétrica.
- Se $n>30$, $\chi_n^2$ pode aproximarse por unha normal $N(n,\sqrt{2n})$; unha aproximación aínda mellor é $\sqrt{2\chi_n^2}-\sqrt{2n-1}\cong N(0,1)$.
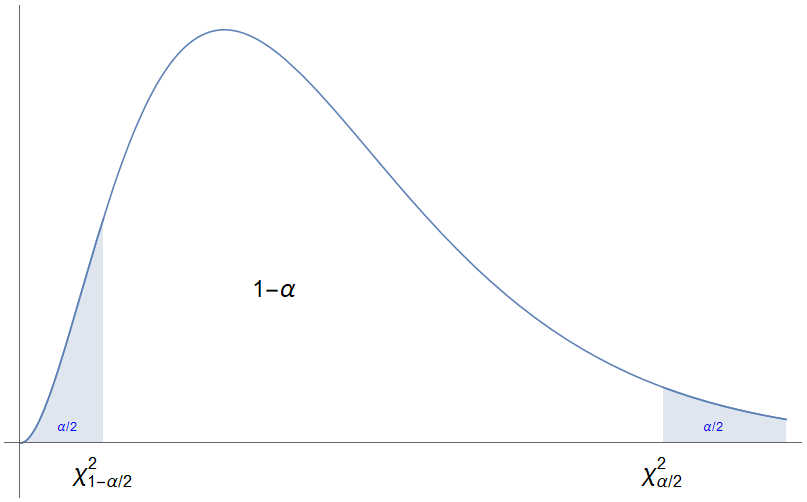
Dado que a distribución $\chi^2$ de Pearson non é simétrica, o intervalo de confianza que construímos tampouco o será. Fixado un nivel de significación $\alpha$, buscamos dous extremos de intervalo $a$ e $b$ de xeito que á esquerda de $a$ e á dereita de $b$ quede probabilidade $\alpha/2$. É dicir, buscámo-los valores $a=\chi^2_{n,\,1-\alpha/2}$ e $b=\chi^2_{n,\,\alpha/2}$ tales que $P(\chi^2_n\geq \chi^2_{n,\,1-\alpha/2})=1-\alpha/2$ e $P(\chi^2_n\geq \chi^2_{n,\,\alpha/2})=\alpha/2$.
Nestas condicións, o intervalo de confianza para a varianza poboacional buscado vén dado pola fórmula \[ \Bigl[\frac{n s_\mu^2}{\chi^2_{n,\,\alpha/2}},\, \frac{n s_\mu^2}{\chi^2_{n,\,1-\alpha/2}}\Bigr]. \]
Como sempre, resulta máis sinxelo, coñecido o estatístico necesario para estima-la varianza poboacional, calcula-lo intervalo de confianza a partir de despexar $\sigma^2$ da inecuación \[ \chi^2_{n,\,1-\alpha/2}\leq \frac{n s_\mu^2}{\sigma^2}\leq \chi^2_{n,\,\alpha/2}, \]
Estimación por intervalos: descoñecida a media poboacional
O procedemento é similar ó caso anterior, pero agora temos que emprega-la cuasi-varianza mostral.
Para estima-la varianza poboacional dunha poboación normal con media descoñecida tomámo-lo estatístico \[ \frac{(n-1) s_{n-1}^2}{\sigma^2}\sim \chi_{n-1}^2, \] que segue unha distribución $\chi^2$ de Pearson con $n-1$ graos de liberdade.
O procedemento para atopar un intervalo de confianza é similar a casos anteriores. De feito, o intervalo de confianza buscado, para unha nivel de significación $\alpha$, é determinado por \[ \chi^2_{n-1,\,1-\alpha/2}\leq \frac{(n-1) s_{n-1}^2}{\sigma^2}\leq \chi^2_{n-1,\,\alpha/2} \]
Despexando $\sigma^2$ obtemos: \[ \Bigl[\frac{(n-1) s_{n-1}^2}{\chi^2_{n-1,\,\alpha/2}},\, \frac{(n-1) s_{n-1}^2}{\chi^2_{n-1,\,1-\alpha/2}}\Bigr]. \]
Obtense unha mostra aleatoria de 100 adultos aparentemente sans co fin de establecer un patrón con respecto ó que se considerará unha lectura normal de calcio. Extráese unha mostra de sangue de cada adulto. A variable estudada é $X$="contido de calcio en mg/dl de sangue", que se supón que presenta unha distribución aproximadamente normal. Obtívose unha media mostral de 9.5mg/dl e unha varianza $s_n^2=0.2475$. Calcular intervalos de confianza do 99% para a media e a desviación típica da poboación.
Considerámo-la variable aleatoria $X$="contido de calcio en mg/dl de sangue".
Os datos que temos no enunciado son o tamaño da mostra $n=100$, a media mostral $\overline{X}=9.5$ e a varianza $s_n^2=0.2475$. A cuasi-varianza é $s_{n-1}^2=\frac{100}{99}\cdot 0.2475=0.25$; logo $s_{n-1}=0.5$. O nivel de significación é $\alpha=0.01$.
Para o cálculo dun intervalo de confianza para a media buscámo-lo valor $t_{99,0.005}=2.63$. Así un intervalo para a media é \[ 9.5\pm 2.63\cdot\frac{0.5}{\sqrt{100}}=9.5\pm 0.13, \] ou ben, $[9.37, 9.63]$.
A continuación pasamos á varianza. Temos que buscar dous valores da $\chi^2$: $\chi_{99,0.005}^2=138.99$ e $\chi_{99,0.995}^2=66.51$. O intervalo de confianza para a varianza é \[ \Bigl[\frac{99\cdot 0.25}{138.99},\frac{99\cdot 0.25}{66.51}\Bigr] =[0.18,0.37]. \] Simplemente extraendo raíces cadradas temos un intervalo de confianza para a desviación típica: $[0.42,0.61]$.
Conclusión: cunha confianza do 99%, o contido en calcio en sangue medido en mg/dl na poboación estudada ten unha media que está comprendida entre 9.37 e 9.63, e unha desviación típica entre 0.42 e 0.61.
Estimación dunha proporción
Supoñamos que temos unha variable con dous posibles valores. Temos unha poboación na que queremos estima-la proporción $p$ de individuos que teñen un deses valores. Unha mostra individual desa poboación seguirá pois unha distribución de Bernoulli de parámetro $p$, mentres que a poboación segue unha distribución binomial de parámetros $N$ (número de elementos) e $p$.
Recordemos que a distribución binomial de parámetros $N$ e $p$ é unha distribución discreta con función de masa \[ P(X=k)=\binom{N}{k}p^k(1-p)^{N-k}. \] A súa media e a súa varianza son \[ \begin{aligned} E(X)&{}=Np,& V(X)&{}=Np(1-p). \end{aligned} \]
Estimación puntual
Queremos construír un estimador $\hat{p}$ de $p$. Para iso definímo-la variable aleatoria $X$ que lle asigna $1$ ó valor que queremos medir, e $0$ ó outro. Escollemos unha mostra aleatoria simple $X_1,\dots,X_n$.
Para estimar unha proporción é razoable toma-lo estimador puntual \[ \hat{p}=\frac{1}{n}\sum_{i=1}^n X_i, \] que aproxima a proporción da característica que queremos medir cos datos da mostra escollida.
Temos que $n\hat{p}=\sum_{i=1}^n X_i$ segue unha distribución binomial de parámetros $n$ e $p$. No caso de que a mostra sexa grande (con $np,n(1-p)\geq 5$ acostuma ser suficiente), podemos aproxima-la binomial por unha normal.
Co obxectivo de estandariza-los cálculos e facer máis inmediato o emprego das táboas realizaremos o procedemento típico de tipifica-la variable.
Por tanto, habitualmente consideraremos que a distribución na mostraxe para estimar unha proporción vén dada por \[ \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\sim Z \] que segue (aproximadamente) unha distribución normal estándar $Z=N(0,1)$.
Satisfaise que \[ \begin{aligned} E(\hat{p})&{}=p,& V(\hat{p})&{}=\frac{p(1-p)}{n}, \end{aligned} \] e por tanto, dise que $\hat{p}$ é un estimador insesgado e consistente de $p$.
Estimación por intervalos
O procedemento para atopar un intervalo de confianza é similar ó explicado para a media, aínda que hai algunha dificultade que presentamos a continuación. Sexa $\alpha$ o nivel de significación. Tomamos $Z_{\alpha/2}$ tal que $P(z\geq Z_{\alpha/2})=\alpha/2$. En principio o cálculo dun intervalo de confianza viría expresado despexando $p$ na fórmula \[ \left\lvert\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\right\rvert\leq Z_{\alpha/2}. \] O problema é que o denominador $\sqrt{p(1-p)/n}$ depende de $p$, que é xusto o que queremos estimar. En consecuencia, aproximaremos $\sqrt{{p(1-p)}/{n}}$ por $\sqrt{{\hat{p}(1-\hat{p})}/{n}}$.
Así un intervalo de confianza para a proporción vén dado pola expresión \[ -Z_{\alpha/2}\leq\frac{\hat{p}-p}{\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}}\leq Z_{\alpha/2}. \]
Despexando $p$ obtemos. \[ \biggl[\,\hat{p}-Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}},\, \hat{p}+Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\,\biggr], \] ou ben, \[ \hat{p}\pm Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}. \]
Un laboratorio desexa averigua-la proporción de cápsulas defectuosas que produce dun determinado medicamento. Para iso selecciona e proba 2000 unidades e descubre un total de 200 unidades defectuosas. Estima-la proporción de cápsulas defectuosas na produción. Calcular un intervalo de confianza ó 95% para a proporción.
Considerámo-la variable aleatoria $X$ que asigna o valor $1$ ás cápsulas defectuosas e $0$ ás correctas.
Tamaño mostral $n=2000$. Estimación puntual da proporción $\hat{p}=200/2000=0.1=10\%$.
Nivel de significación: $\alpha=0.05$. Buscámo-lo valor $Z_{0.025}$ tal que $P(Z\geq Z_{0.025})=0.025$. Aproximadamente, $Z_{0.025}=1.96$.
O intervalo de confianza buscado é entón \[ 0.1\pm 1.96\sqrt{\frac{0.1(1-0.1)}{2000}}=0.1\pm 0.0131, \] que explicitamente, en termos de porcentaxes, é $[8.69\%,11.31\%]$.
Conclusión: cunha confianza do 95%, a porcentaxe de cápsulas defectuosas na producción do laboratorio sitúase entre o 8.69% e o 11.31%.
Determinación do tamaño da mostra
En vista do intervalo de confianza construído para a proporción, o erro cometido ó tomar $\hat{p}$ en lugar do valor verdadeiro $p$ estímase que é \[ Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \] que depende do tamaño mostral $n$, do nivel de confianza $\alpha$, e de $\sqrt{\hat{p}(1-\hat{p})}$. Se coñecemos (ou podemos estimar con precisión) o valor de $\hat{p}$, bastaría impoñer que a anterior fórmula é $<\epsilon$ e despexar $n$.
Cando o valor de $\hat{p}$ non é coñecido pode estimarse o tamaño da mostra necesario para limita-lo erro, se ben o valor obtido será máis grande que cando $\hat{p}$ é coñecido. No intervalo $[0,1]$ pode verse, empregando as técnicas do cálculo, que o máximo de $\sqrt{x(1-x)}$ está en $x=1/2$, de xeito que teremos sempre \[ Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\leq Z_{\alpha/2}\sqrt{\frac{0.5(1-0.5)}{n}}. \] Se queremos que o erro sexa menor ca $\epsilon$, basta entón impoñe-la condición \[ Z_{\alpha/2}\sqrt{\frac{0.5(1-0.5)}{n}}<\epsilon, \] de onde resulta \[ n> \frac{Z_{\alpha/2}^2}{4\epsilon^2}. \]
Para toma-la decisión de someter ou non a referendo unha lei, o goberno dun certo país necesita encargar un estudo sobre a porcentaxe de votantes que a apoiaría. Dada a importancia política da mesma e a polémica xurdida, necesita unha estimación do voto cun erro menor do 1%. ¿Cal sería o tamaño mostral mínimo requerido para un nivel de confianza do 99%?
Considerámo-la variable aleatoria $X$="intención de voto".
Para estima-lo tamaño da mostra para unha proporción, empregámo-lo estatístico \[ \frac{\hat{p}-p}{\sqrt{\frac{p \left(1-p\right)}{n}}}, \] que segue unha distribución normal estándar. Despexando $p$ da desigualdade \[ \left\lvert \frac{\hat{p}-p}{\sqrt{\frac{\hat{p} \left(1-\hat{p}\right)}{n}}} \right\rvert \leq Z_{\alpha/2}, \] obtense a fórmula \[ \hat{p} \pm Z_{\alpha/2} \sqrt{\frac{\hat{p} \left(1-\hat{p}\right)}{n}}. \] A estimación do erro é \[ Z_{\alpha/2} \sqrt{\frac{\hat{p} \left(1-\hat{p}\right)}{n}}. \]
Neste caso non temos unha estimación da proporción $\hat{p}$. É sinxelo ver que a función $x\mapsto\sqrt{x(1-x)}$ alcanza o seu máximo no intervalo $[0,1]$ no punto $x=1/2$. Por tanto, necesitamos despexar $n$ da desigualdade $Z_{\alpha/2}\sqrt{\frac{0.5(1-0.5)}{n}} \leq \epsilon$, onde $\epsilon$ é o valor fixado polo problema. Así, obtense $n \geq \left(\frac{Z_{\alpha/2}}{2 \epsilon}\right)^{2}$.
O nivel de significación é $\alpha=0.01$. Calculamos $Z_{0.005}=2.5758$. Neste caso $\epsilon=0.01$. Substituíndo na fórmula, $n \geq \left(\frac{2.5758}{2\cdot 0.01}\right)^{2} = 16587.2415$.
Conclusión: para que a diferencia entre a proporción mostral e a proporción poboacional de intención de voto sexa como moito dun $\pm 1\%$ cun nivel de confianza do $99$%, teriamos que tomar unha mostra de polo menos $16588$ persoas.
Resumo de estimadores
Táboa resumo cos resultados explicados neste capítulo.