Regresión e correlación
O obxectivo deste capítulo é tratar de establece-la dependencia dunhas variables aleatorias con outras. En principio asumiremos que un determinado efecto se pode explicar mediante unhas causas e un erro. Asumiremos que temos dúas variables aleatorias $X$ e $Y$. O obxectivo é atopar unha función $f$ tal que $Y=f(X)+\epsilon$. Así, a $Y$ chámaselle resposta, a $f$ a explicación, e $\epsilon$ é o erro.
O seguinte gráfico amosa tres nubes de puntos distintas obtidas despois de tomar unha mostra aleatoria de dúas variables $X$ e $Y$. No primeiro caso é evidente que non existe moita relación entre as dúas variables. No segundo caso parece que as variables están bastante relacionadas, e salvo un pequeno erro, dá a impresión de que $Y$ se explica como dependente de $X$ a través dunha ecuación polinómica. Finalmente, a terceira nube de puntos semella que se axusta a unha recta, aínda que o erro cometido é considerablemente máis grande ca no segundo exemplo.
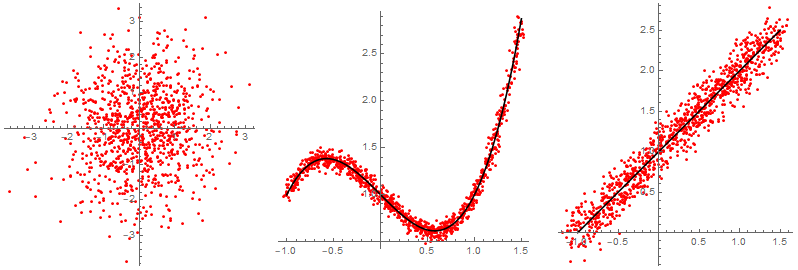
Nos dous últimos debuxos anteriores, é claro que existe unha dependencia (máis ou menos forte) entre $X$ e $Y$. O obxectivo dun modelo de regresión é:
- Coñecer de que xeito a variable $Y$ depende de $X$. Isto é o que se chama construír un modelo de regresión.
- Unha vez construído o modelo de regresión, empregar este para determina-lo valor de $Y$ cando o valor de $X$ é coñecido.
Neste capítulo consideraremos soamente o caso do modelo de regresión linear simple, que é aquel no que as variables $X$ e $Y$ son unidimensionais (como habitualmente), e que $Y$ se explica a partir de $X$ mediante a ecuación dunha recta (coma no terceiro debuxo). Tamén se tratarán outros modelos que se reducen facilmente do de regresión linear.
Regresión linear
Sexan $X$ e $Y$ dúas variables aleatorias. O modelo de regresión linear consiste en atopa-la recta $y=\alpha+\beta x$ que minimiza \[ E\bigl[(Y-(\alpha+\beta X))^2\bigr], \] onde o que se trata é de atopar $\alpha$ e $\beta$.
Non é difícil ver que estes dous valores se poden calcular simplemente derivando a anterior expresión con respecto de $\alpha$ e de $\beta$ e igualando a cero. (Analogamente a como se fai para calcula-lo mínimo dunha función, pero con dúas variables.) Esta recta chámase a recta de regresión mínimo-cuadrática, porque na práctica se obtén despois de minimiza-la distancia cuadrática media dos puntos dunha mostra a dita recta.
Despois de face-los cálculos resulta que a ecuación da recta buscada é \[ Y-\mu_Y=\frac{\sigma_{XY}}{\sigma_X^2}(X-\mu_X)+\epsilon, \] onde
- $\mu_X=E[X]$ é a media de $X$,
- $\mu_Y=E[Y]$ é a media de $Y$,
- $\sigma_X^2=E[(X-\mu_X)^2]$ é a varianza de $X$,
- $\sigma_Y^2=E[(Y-\mu_Y)^2]$ é a varianza de $Y$,
- $\sigma_{XY}=E[(X-\mu_X)(Y-\mu_Y)]=E[XY]-E[X]E[Y]$ é a covarianza entre $X$ e $Y$,
- $\epsilon$ é unha variable aleatoria que representa o erro cometido.
É consecuencia da construción do modelo que o erro ten media cero $\mu_\epsilon=E[\epsilon]=0$, e que a súa varianza $\sigma_\epsilon^2=V[\epsilon]$ é mínima.
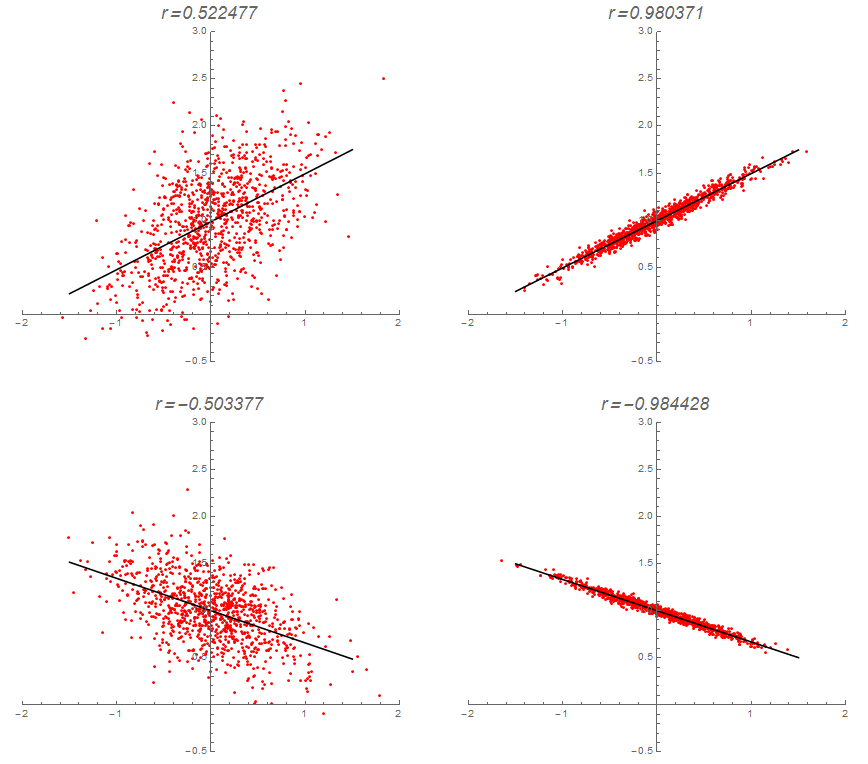
Defínese o coeficiente de correlación de Pearson coma o cociente \[ \rho=\frac{\sigma_{XY}}{\sigma_X \sigma_Y}, \] que satisfai $-1\leq\rho\leq 1$, e dá unha idea do bo que é o axuste.
Estimación dos valores
Na práctica as variables aleatorias $X$ e $Y$ non son coñecidas e son estimadas por valores concretos $(x_1,y_1),\dots,(x_n,y_n)$ dunha mostra.
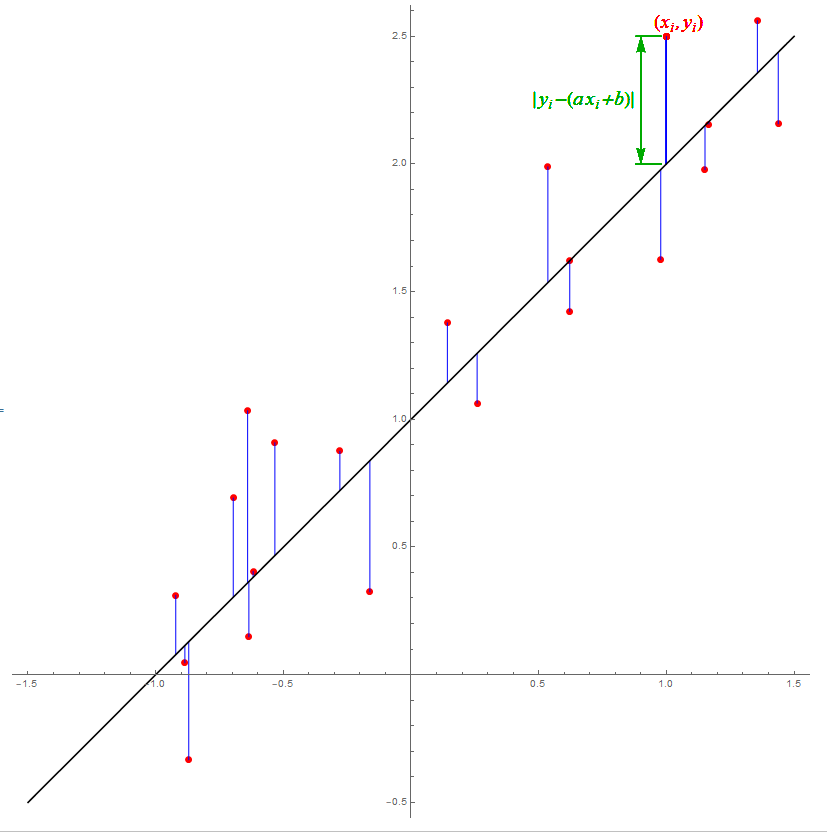
Para estima-lo modelo regresión linear tratamos de minimiza-la distancia cadrática media dos puntos da mostra á recta de regresión. Por iso, o modelo de regresión linear estímase como \[ Y-\overline{y}=\frac{s_{XY}}{s_X^2}(X-\overline{x})+\epsilon, \] onde agora \[ \begin{aligned} \overline{x}&{}=\frac{1}{n}\sum_{i=1}^n x_i,\\ \overline{y}&{}=\frac{1}{n}\sum_{i=1}^n y_i,\\ s_X^2&{}=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2 =\frac{1}{n}\sum_{i=1}^n x_i^2-\overline{x}^2,\\ s_Y^2&{}=\frac{1}{n}\sum_{i=1}^n(y_i-\overline{y})^2 =\frac{1}{n}\sum_{i=1}^n y_i^2-\overline{y}^2,\\ s_{XY}&{}=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y}) =\frac{1}{n}\sum_{i=1}^n x_i y_i-\overline{x}\,\overline{y}. \end{aligned} \]
Unha estimación equivalente para a recta de regresión é: \[ Y=a+bX+\epsilon, \] onde \[ \begin{aligned} b&{}=\hat{\beta}=\frac{s_{XY}}{s_X^2},\\ a&{}=\hat{\alpha}=\overline{y}-b\,\overline{x}. \end{aligned} \]
Nótese que esta recta de regresión sempre pasa por $(\overline{x},\overline{y})$.
Covarianza e correlación
A covarianza é a forma máis común de medi-la relación linear entre dúas variables. Para datos concretos recordemos que se estima por \[ \begin{aligned} s_{XY}&{}=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})\\ &{}=\frac{1}{n}\sum_{i=1}^n x_i y_i-\overline{x}\,\overline{y}. \end{aligned} \]
A covarianza non se ve afectada por cambios de posición, pero si de escala. De feito, \[ s_{aX+b,\,cY+d}=ac\, s_{XY}. \]
Para obter unha medida da relación linear entre dúas variables que non dependa da escala introduciuse o coeficiente de correlación, que para datos concretos se estima mediante \[ r=\frac{s_{XY}}{s_X s_Y}. \]
Unha versión equivalente, pero máis estable numericamente, é \[ r=\frac{\displaystyle n\sum_{i=1}^n x_i y_i-\Bigl(\sum_{i=1}^n x_i\Bigr)\Bigl(\sum_{i=1}^n y_i\Bigr)} {\sqrt{\displaystyle n\sum_{i=1}^n x_i^2-\Bigl(\sum_{i=1}^n x_i\Bigr)^2}\, \sqrt{\displaystyle n\sum_{i=1}^n y_i^2-\Bigl(\sum_{i=1}^n y_i\Bigr)^2}}. \]
O coeficiente de correlación satisfai as seguintes propiedades:
- O coeficiente de correlación ten o mesmo signo cá pendente da recta de regresión.
- $-1\leq r\leq 1$; valores próximos a $0$ indican que o axuste é malo, valores próximos a $1$ indican que o axuste é bo e que a relación é crecente, mentres que valores próximos a $-1$ indican que o axuste é bo e que a relación é decrecente.
Un rango de valores para a bondade do axuste en función de $r$ pode se-lo seguinte:
Algúns exemplos de coeficientes de correlación poden verse na táboa adxunta.
Os seguintes datos correspóndense co tempo transcorrido e a velocidade de caída dun obxecto:
| tempo | velocidade |
|---|---|
| 1 | 20.52 |
| 2 | 29.14 |
| 3 | 36.76 |
| 4 | 47.80 |
| 5 | 58.72 |
Calcula-la recta de regresión e dar unha aproximación da aceleración da gravidade. ¿Como de bo é o axuste?
Temos dúas variables que chamaremos $t$ (tempo) e $v$ (velocidade). En primeiro lugar dispoñémo-los cálculos:
| $t$ | $v$ | $t^2$ | $tv$ | $v^2$ | |
| 1. | 20.52 | 1. | 20.52 | 421.07 | |
| 2. | 29.14 | 4. | 58.28 | 849.14 | |
| 3. | 36.76 | 9. | 110.28 | 1351.30 | |
| 4. | 47.80 | 16. | 191.20 | 2284.84 | |
| 5. | 58.72 | 25. | 293.60 | 3448.04 | |
| $\Sigma$ | 15. | 192.94 | 55. | 673.88 | 8354.39 |
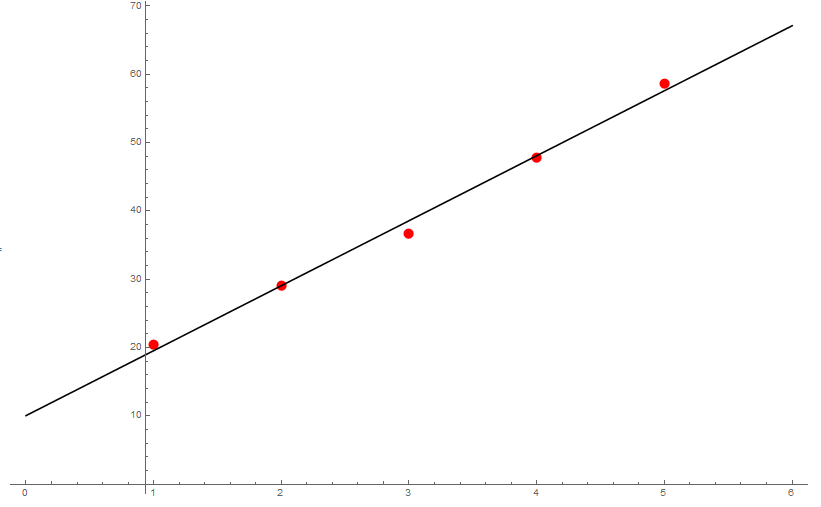
Entón \[ \begin{aligned} \overline{t} &{}=\frac{15.}{5}=3.0,\\ \overline{v} &{}=\frac{192.94}{5}=38.59,\\ s_t^2 &{}=\frac{55.}{5}-3^2=2.0,\\ s_v^2 &{}=\frac{8354.39}{5}-38.59^2=181.84,\\ s_{tv} &{}=\frac{673.88}{5}-3\cdot 38.59=19.01, \end{aligned} \] co que, substituíndo na fórmula, obtémo-la recta de regresión $v-38.59=\frac{19.01}{2}(t-3)$, ou ben, como $b=19.01/2.0=9.51$ e $a=38.59-9.51\cdot 3.0=10.07$, que \[ v=10.07+9.51t, \] de onde ademais se deduce que, en vista do resultado coñecido de física $v=v_0+gt$, que $g=9.51$ é unha aproximación da aceleración da gravidade.

Finalmente calculámo-lo coeficiente de correlación: \[ r=\frac{19.01}{\sqrt{2}\sqrt{181.84}}=0.997, \] o cal quere dicir que o axuste é bo.
Regresión exponencial
O procedemento para calcular unha regresión linear pode ser empregado tamén noutros contextos simplemente facendo un pequeno cambio de variable. Por exemplo, supoñamos que temos dúas variables aleatorias $Z$ e $T$, e cremos que $Z$ se explica a partir de $T$ a través dunha fórmula exponencial: \[ Z=z_0\, e^{-kT}, \] onde $z_0$ e $k$ son os parámetros que queremos determinar. Entón, tomando logaritmos (neperianos) \[ \begin{aligned} \log Z &{}=\log\bigl(z_0 e^{-kT}\bigr) =\log z_0-kT. \end{aligned} \] Chamando $Y=\log Z$, $X=T$, $b=-k$, $a=\log z_0$, estamos exactamente na situación $Y=a+bX$ do principio. Por tanto, este tipo de axuste exponencial redúcese a un axuste linear, que xa sabemos resolver.
Inxectamos por vía intravenosa $125mg$ dun medicamento. Témo-las seguintes concentracións plasmáticas a medida que pasa o tempo:
| tempo | concentración |
|---|---|
| 1 | 5.0 |
| 2 | 3.0 |
| 3 | 2.0 |
| 4 | 1.5 |
Queremos estima-la curva exponencial da concentración de medicamento en sangue.
É sabido que a evolución da concentración teórica $C$ dun medicamento en sangue ó longo do tempo $t$ segue unha curva exponencial $C=c_0\,e^{-kt}$. Despois de tomar logaritmos neperianos temos $\log C=\log c_0-k t$, así que para calcula-la recta de regresión destes datos organizámo-los cálculos do seguinte xeito:
| $X=t$ | $C$ | $Y=\log C$ | $X^2$ | $XY$ | $Y^2$ | |
| 1. | 5.0 | 1.61 | 1. | 1.61 | 1.59 | |
| 2. | 3.0 | 1.10 | 4.0 | 2.20 | 1.21 | |
| 3. | 2.0 | 0.69 | 9.0 | 2.08 | 0.48 | |
| 4. | 1.5 | 0.41 | 16.0 | 1.62 | 0.16 | |
| $\Sigma$ | 10. | 11.5 | 3.81 | 30.0 | 7.51 | 4.44 |
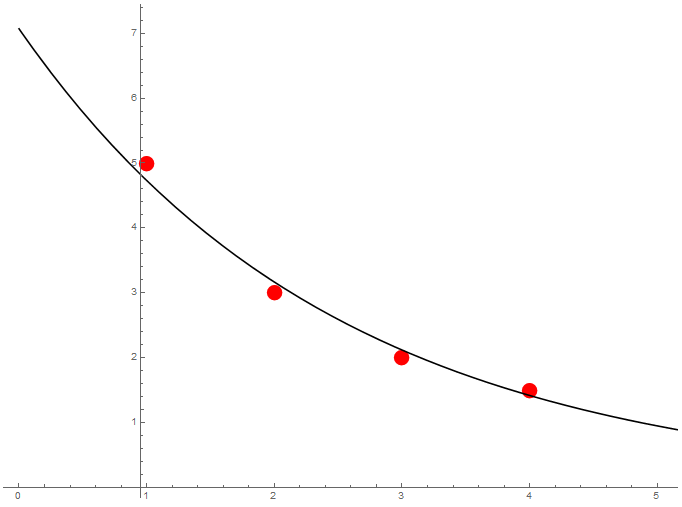
Entón \[ \begin{aligned} \overline{X} &{}=\frac{10.}{4}=2.5,\\ \overline{Y} &{}=\frac{3.81}{4}=0.95,\\ s_X^2 &{}=\frac{30.0}{4}-2.5^2=1.25,\\ s_Y^2 &{}=\frac{4.44}{4}-0.95^2=0.20,\\ s_{XY} &{}=\frac{7.51}{4}-2.5\cdot 0.95=-0.50, \end{aligned} \] co que, substituíndo na fórmula, obtémo-la recta de regresión: \[ Y-0.95=-\frac{0.50}{1.25}(X-2.5). \] Equivalentemente, obtense $b=-0.50/1.25=-0.40$, $a=0.95+0.40\cdot 2.5=1.96$, de onde se deduce $Y=1.96-0.40 X$, ou $\log C=1.96-0.40t$. Desfacendo o cambio de variable obtemos \[ C=7.07e^{-0.40t}. \]
Pódese ver ademais que o coeficiente de correlación é \[ r=\frac{-0.50}{\sqrt{1.25}\sqrt{0.20}}=-0.992, \] o que, ademais dun bo axuste, indica que a variable $Y$ (ou a concentración $C$) decrece en función do tempo.
Regresión potencial
A regresión potencial é un caso bastante parecido ó da regresión exponencial. Neste caso hai dúas variables $P$ e $A$ que están relacionadas mediante a fórmula \[ P=\alpha A^\beta. \] Para resolver isto, tomamos coma na sección anterior logaritmos e obtemos \[ \log P=\log\bigl(\alpha A^\beta\bigr) =\log \alpha+\beta\log A. \] Así, chamando $Y=\log P$ e $X=\log A$ volvemos estar nun caso de axuste linear, que xa vimos como se resolve.
Análise da varianza
O obxectivo desta sección é estudar con máis profundidade se o modelo de regresión construído é correcto e útil. Para iso imos empregar un método coñecido como ANOVA (analysis of variance).
En primeiro lugar recordamos que $Y=\alpha+\beta X+\epsilon$, onde $\hat{Y}=\alpha+\beta X$ será a estimación dada pola recta de regresión, e $\epsilon=Y-\hat{Y}$ é o erro. Un cálculo non trivial amosa que as varianzas están relacionadas mediante \[ \sigma_Y^2=\sigma_{\hat{Y}}^2+\sigma_\epsilon^2. \] Isto significa que a variabilidade da variable dependente $Y$, $\sigma_Y^2$, se descompón como
- A variabilidade explicada, $\sigma_{\hat{Y}}^2$, que é aquela que se pode explicar en base ó modelo de regresión. De feito, como $\hat{Y}=\alpha+\beta X$, entón $\sigma_{\hat{Y}}^2=\beta^2\sigma_X^2$.
- A variabilidade residual, $\sigma_\epsilon^2$, que é a que non explica o modelo de regresión.
Chámase coeficiente de determinación á proporción entre a variabilidade explicada e a variabilidade da variable dependente. Por tanto, \[ \frac{\sigma_{\hat{Y}}^2}{\sigma_Y^2}=\frac{\beta^2\sigma_X^2}{\sigma_Y^2} =\frac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2, \] que é o cadrado do coeficiente de correlación. Por tanto, $0\leq \rho^2\leq 1$.
Como xa sucedía co coeficiente de correlación, se $\rho^2=1$ (é dicir, se $\rho=\pm 1$) entón o axuste é perfecto. Valores de $\rho^2$ próximos a $1$ significan que o axuste é bo, mentres que valores próximos a $0$ indican un axuste malo.
Ademais, das fórmulas anteriores temos que \[ \begin{aligned} \sigma_{\hat{Y}}^2 &{}=\rho^2 \sigma_Y^2,\\[1ex] \sigma_\epsilon^2 &{}=\sigma_Y^2-\sigma_{\hat{Y}}^2 =\sigma_Y^2-\rho^2\sigma_Y^2=(1-\rho^2)\sigma_Y^2. \end{aligned} \]
ANOVA
En realidade, os cálculos da sección anterior son teóricos, porque en xeral as distribucións $X$ e $Y$ non son coñecidas. Na práctica tómase unha mostra e utilízanse as estimacións escritas con anterioridade.
Para continuar supoñamos que estamos traballando con $n$ valores específicos $x_1,\dots,x_n$. Por tanto, os valores da variable explicativa están fixados polo experimentador e non son aleatorios. Só é aleatorio o erro, e en consecuencia a variable resposta. Unha mostra resultante deste tipo de experimento (chamado de deseño fixo), é do tipo $(x_1,Y_1),\dots,(x_n,Y_n)$. Asumimos que as variables aleatorias $Y\mid X=x_1,\dots,Y\mid X=x_n$ seguen distribucións normais independentes coa mesma varianza $\sigma^2$. Se a regresión linear é válida, as medias destas variables están xustamente en $a+bx_i$, é dicir, $(Y\mid X=x_i)\sim N(a+bx_i,\sigma)$.
O valor $\hat{Y}_i$ será o valor predecido pola estimación do modelo, é dicir, $\hat{Y}_i=a+bx_i$. Nótese en particular que $\overline{\hat{Y}}=\overline{Y}=a+b\overline{x}$.
Así, despois de multiplicar por $n$, a variabilidade é estimada mediante \[ \sum_{i=1}^n(Y_i-\overline{Y})^2= \sum_{i=1}^n(\hat{Y}_i-\overline{Y})^2+\sum_{i=1}^n(Y_i-\hat{Y}_i)^2. \] Se agora denotamos \[ \begin{aligned} SS_Y&{}=\sum_{i=1}^n(Y_i-\overline{Y})^2,\\ SS_R&{}=\sum_{i=1}^n(\hat{Y}_i-\overline{Y})^2=b^2\sum_{i=1}^n(x_i-\overline{x})^2,\\ SS_E&{}=\sum_{i=1}^n(Y_i-\hat{Y}_i)^2, \end{aligned} \] entón, a expresión anterior pode escribirse como
| $SS_Y$ | = | $SS_R$ | + | $SS_E$ |
| (variabilidade total) | (variabilidade debida á regresión) | (variabilidade non explicada) |
As fórmulas anteriores refírense ás "sumas de cadrados". Se en lugar diso querémo-las varianzas, simplemente hai que dividir polo tamaño mostral $n$: \[ \begin{aligned} s_Y^2&{}=\frac{1}{n}SS_Y,& s_{R}^2&{}=\frac{1}{n}SS_R,& s_E^2&{}=\frac{1}{n}SS_E.\\ \end{aligned} \] Estas cantidades son unha estimación das varianzas teóricas obtidas no apartado anterior. Por outra banda, o coeficiente de determinación estímase mediante $r^2$, de xeito que temos \[ r^2=\frac{s_R^2}{s_Y^2}=\frac{SS_R}{SS_Y}. \] Así, a estimación do coeficiente de determinación $r^2$ interprétase como a proporción da variabilidade da variable aleatoria $Y$ que é explicada por $X$ mediante o modelo de regresión.
Esta técnica de análise da varianza utilízase para comprobar se unha liña recta mostra unha cantidade significativa de variabilidade observada de $Y$. Se o suposto é que a regresión é válida, entón o que terá que suceder é que a maior parte da variabilidade terá que ser explicada por $SS_R$, sendo a parte non explicada pequena.
Obsérvese agora a equivalencia das seguintes condicións \[ \beta=0\Leftrightarrow\rho=0, \] é dicir, toda a variabilidade é aleatoria (non explicada), e por tanto non hai regresión linear. Así pois, o test que temos que facer para comproba-la validez do modelo é \[ \begin{aligned} H_0\colon\, &\rho=0,& H_1\colon\, &\rho\neq 0. \end{aligned} \]
Baixo as hipóteses anteriores, este contraste emprega dous estatísticos que pasamos a describir a continuación. En primeiro lugar, para $SS_Y$ hai $n$ datos e un valor estimado, $\overline{Y}$, o que deixa $n-1$ graos de liberdade.
- Para $SS_E$ hai $n$ datos, pero dous valores estimados, $a$ e $b$, o que nos deixa $n-2$ graos de liberdade. Así, empregamos como estatístico o cadrado medio do erro: $\displaystyle MS_E=\frac{SS_E}{n-2}$.
- Iso significa que para $SS_R$ queda un só grao de liberdade. O estatístico empregado é pois o cadrado medio da regresión: $\displaystyle MS_R=\frac{SS_R}{1}$.
No suposto de que a hipótese nula sexa certa, o estatístico \[ \frac{MS_R}{MS_E} =\frac{\sum_{i=1}^n(\hat{Y}_i-\overline{Y})^2}{\sum_{i=1}^n(Y_i-\hat{Y}_i)^2/(n-2)} \sim F_{1,\,n-2} \] segue unha distribución $F$ de Snedecor con $(1,n-2)$ graos de liberdade.
Se a hipótese nula é certa, o valor observado no estatístico estará próximo a 1. Noutro caso será moito maior e rexeitarase a hipótese nula se o valor é demasiado grande. Trátase por tanto de facer un contraste unilateral dereito.
Os cálculos necesarios para empregar ANOVA á hora de contrastar $H_0\colon\rho=0$ (non hai regresión linear), dispóñense nunha táboa como a seguinte:
| variabilidade | g.l. | $SS$ | $MS$ | cociente |
|---|---|---|---|---|
| regresión | $1$ | $\displaystyle SS_R=\sum_{i=1}^n(\hat{Y}_i-\overline{Y})^2=n r^2 s_Y^2$ | $\displaystyle MS_R=\frac{SS_R}{1}$ | $\displaystyle F_{1,\,n-2}=\frac{MS_R}{MS_E}$ |
| erro | $n-2$ | $\displaystyle SS_E=\sum_{i=1}^n(Y_i-\hat{Y}_i)^2=n(1-r^2)s_Y^2$ | $\displaystyle MS_E=\frac{SS_E}{n-2}$ | |
| total | $n-1$ | $\displaystyle SS_Y=\sum_{i=1}^n(Y_i-\overline{Y})^2=ns_Y^2$ |
Cando, despois de face-lo anterior contraste de hipóteses, cheguemos á conclusión de que se rexeita a hipótese nula $H_0$, iso quererá dicir que unha parte significativa da variabilidade de $Y$ se pode explicar mediante o modelo de regresión linear. Iso non quere dicir que o modelo linear sexa o mellor para explicar dita variabilidade, senón que é razoable emprega-lo modelo para explicala.
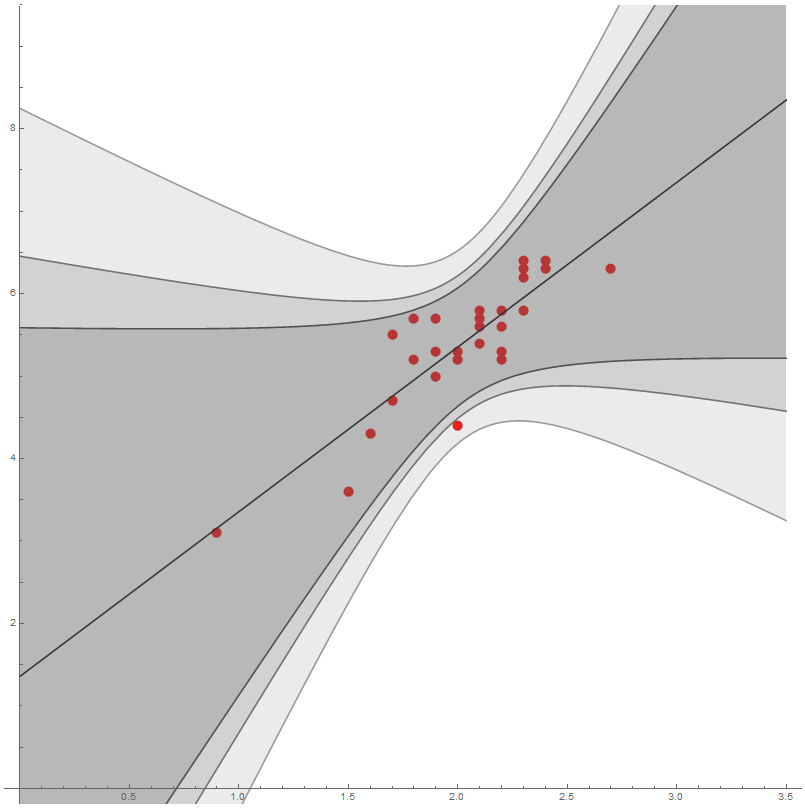
Realízase un experimento para estuda-la relación entre a altura e a lonxitude da cuncha de Patelloida pygmaea (en mm). Téñense os seguinte datos:
| altura | lonxitude | altura | lonxitude | altura | lonxitude | altura | lonxitude |
|---|---|---|---|---|---|---|---|
| 0.9 | 3.1 | 1.9 | 5.0 | 2.1 | 5.6 | 2.3 | 5.8 |
| 1.5 | 3.6 | 1.9 | 5.3 | 2.1 | 5.7 | 2.3 | 6.2 |
| 1.6 | 4.3 | 1.9 | 5.7 | 2.1 | 5.8 | 2.3 | 6.3 |
| 1.7 | 4.7 | 2.0 | 4.4 | 2.2 | 5.2 | 2.3 | 6.4 |
| 1.7 | 5.5 | 2.0 | 5.2 | 2.2 | 5.3 | 2.4 | 6.4 |
| 1.8 | 5.7 | 2.0 | 5.3 | 2.2 | 5.6 | 2.4 | 6.3 |
| 1.8 | 5.2 | 2.1 | 5.4 | 2.2 | 5.8 | 2.7 | 6.3 |
| altura | lonxitude |
|---|---|
| 0.9 | 3.1 |
| 1.5 | 3.6 |
| 1.6 | 4.3 |
| 1.7 | 4.7 |
| 1.7 | 5.5 |
| 1.8 | 5.7 |
| 1.8 | 5.2 |
| 1.9 | 5.0 |
| 1.9 | 5.3 |
| 1.9 | 5.7 |
| 2.0 | 4.4 |
| 2.0 | 5.2 |
| 2.0 | 5.3 |
| 2.1 | 5.4 |
| 2.1 | 5.6 |
| 2.1 | 5.7 |
| 2.1 | 5.8 |
| 2.2 | 5.2 |
| 2.2 | 5.3 |
| 2.2 | 5.6 |
| 2.2 | 5.8 |
| 2.3 | 5.8 |
| 2.3 | 6.2 |
| 2.3 | 6.3 |
| 2.3 | 6.4 |
| 2.4 | 6.4 |
| 2.4 | 6.3 |
| 2.7 | 6.3 |
Estima-la recta de regresión da lonxitude como función da altura. Calcula-lo coeficiente de determinación e interpreta-lo seu valor. ¿Hay evidencia estatística de que o modelo de regresión linear é válido?
Chamemos $X$ á altura e $Y$ á lonxitude. Organizámo-los cálculos nunha táboa.
| $X$ | $Y$ | $X^2$ | $XY$ | $Y^2$ | |
|---|---|---|---|---|---|
| 0.90 | 3.10 | 0.81 | 2.79 | 9.61 | |
| 1.50 | 3.60 | 2.25 | 5.40 | 12.96 | |
| 1.60 | 4.30 | 2.56 | 6.88 | 18.49 | |
| 1.70 | 4.70 | 2.89 | 7.99 | 22.09 | |
| 1.70 | 5.50 | 2.89 | 9.35 | 30.25 | |
| 1.80 | 5.70 | 3.24 | 10.26 | 32.49 | |
| 1.80 | 5.20 | 3.24 | 9.36 | 27.04 | |
| 1.90 | 5.00 | 3.61 | 9.50 | 25.00 | |
| 1.90 | 5.30 | 3.61 | 10.07 | 28.09 | |
| 1.90 | 5.70 | 3.61 | 10.83 | 32.49 | |
| 2.00 | 4.40 | 4.00 | 8.80 | 19.36 | |
| 2.00 | 5.20 | 4.00 | 10.40 | 27.04 | |
| 2.00 | 5.30 | 4.00 | 10.60 | 28.09 | |
| 2.10 | 5.40 | 4.41 | 11.34 | 29.16 | |
| 2.10 | 5.60 | 4.41 | 11.76 | 31.36 | |
| 2.10 | 5.70 | 4.41 | 11.97 | 32.49 | |
| 2.10 | 5.80 | 4.41 | 12.18 | 33.64 | |
| 2.20 | 5.20 | 4.84 | 11.44 | 27.04 | |
| 2.20 | 5.30 | 4.84 | 11.66 | 28.09 | |
| 2.20 | 5.60 | 4.84 | 12.32 | 31.36 | |
| 2.20 | 5.80 | 4.84 | 12.76 | 33.64 | |
| 2.30 | 5.80 | 5.29 | 13.34 | 33.64 | |
| 2.30 | 6.20 | 5.29 | 14.26 | 38.44 | |
| 2.30 | 6.30 | 5.29 | 14.49 | 39.69 | |
| 2.30 | 6.40 | 5.29 | 14.72 | 40.96 | |
| 2.40 | 6.40 | 5.76 | 15.36 | 40.96 | |
| 2.40 | 6.30 | 5.76 | 15.12 | 39.69 | |
| 2.70 | 6.30 | 7.29 | 17.01 | 39.69 | |
| $\Sigma$ | 56.60 | 151.10 | 117.68 | 311.96 | 832.85 |
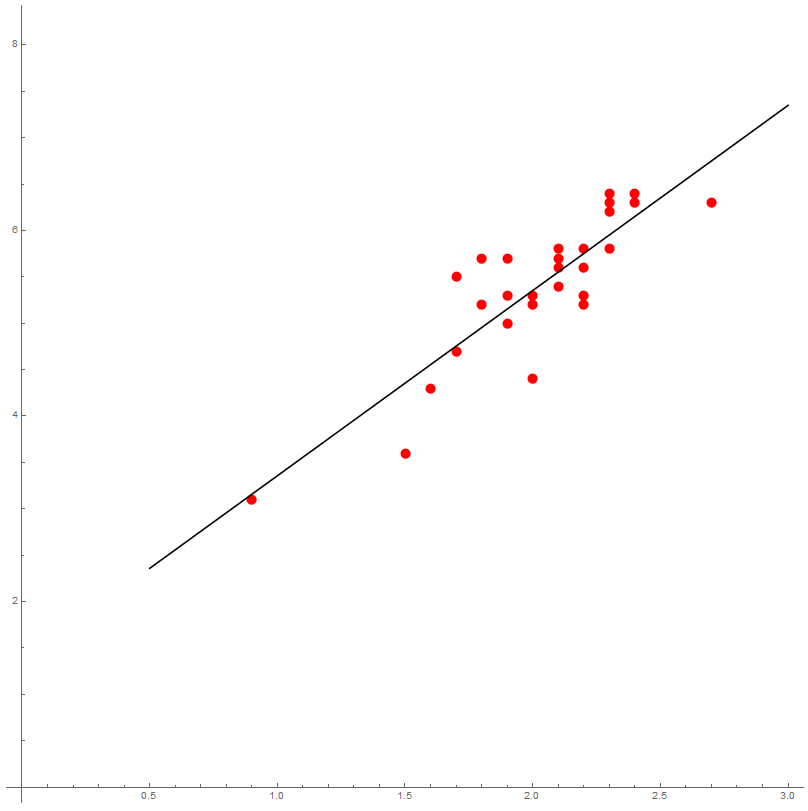
Entón temos $n=28$ datos e \[ \begin{aligned} \overline{X} &{}=\frac{56.6}{28}=2.021,\\ \overline{Y} &{}=\frac{151.10}{28}=5.396,\\ s_X^2 &{}=\frac{117.68}{28}-2.021^2=0.117,\\ s_Y^2 &{}=\frac{832.85}{28}-5.396^2=0.623,\\ s_{XY} &{}=\frac{311.96}{28}-2.021\cdot 5.396=0.233. \end{aligned} \] Obtemos $b=0.233/0.117=1.996$ e $a=5.396-1.996\cdot 2.020=1.361$ co que a ecuación da recta de regresión é \[ y -5.396 = 1.996 (x -2.0214), \] ou ben, \[ y = 1.361 + 1.996 x. \]
A estimación do coeficiente de correlación é \[ r=\frac{0.233}{\sqrt{0.117\cdot 0.623}}=0.8638, \] de xeito que a calidade da aproximación parece moderada.
A estimación do coeficiente de determinación é $r^2=0.746$. Isto interprétase do seguinte xeito: o 74.6% da variabilidade da variable $Y$ está explicada polo modelo de regresión.
Para asegurarnos, intentaremos dar evidencia significativa de que o modelo de regresión é válido. Isto significa face-lo contraste de hipóteses \[ \begin{aligned} H_0\colon &{}\,\rho=0,& H_1\colon &{}\,\rho\neq 0. \end{aligned} \]
Empregamos pois a técnica de análise da varianza, ANOVA. Os datos necesarios están recollidos na seguinte táboa:
| variabilidade | g.l. | $SS$ | $MS$ | cociente |
|---|---|---|---|---|
| regresión | $1$ | $SS_R=28\cdot 0.864^2\cdot 0.623=13.02$ | $MS_R=13.02$ | $76.42$ |
| erro | $26$ | $SS_E=28(1-0.864^2)0.623=4.43$ | $MS_E=\frac{4.43}{26}=0.17$ | |
| total | $27$ | $SS_Y=28\cdot 0.623=17.45$ |
Como $P=P(F_{1,26}\geq 76.42)< 0.01$ é un número moi pequeno (de feito, empregando software estatístico temos $P=3.2\cdot 10^{-9}$), rexeitámo-la hipótese nula. Concluímos que hai evidencia significativa de que o modelo de regresión linear é válido.
Intervalos de estimación
Por completitude incluímos nesta sección a estimación por intervalos de diversos valores que apareceron no noso modelo de regresión linear.
En primeiro lugar pódese ver que unha estimación puntual da desviación típica do erro $\sigma^2$ vén dada por \[ \hat{\sigma}^2=MS_E=\frac{SS_E}{n-2}=\frac{1}{n-2}\sum_{i=1}^n(Y_i-a-bx_i)^2, \] tendo o estatístico \[ \frac{(n-2)\hat{\sigma}^2}{\sigma^2} \] unha distribución $\chi^2$ con $n-2$ graos de liberdade.
Tomemos un nivel de significación $\alpha$.
- Ordenada na orixe: \[ \alpha=a\pm t_{n-2,\,\alpha/2}\,\frac{\sqrt{MS_E}}{S_X}\sqrt{\frac{1}{n}\sum_{i=1}^n x_i^2}. \]
- Pendente da recta de regresión: \[ \beta=b\pm t_{n-2,\,\alpha/2}\,\frac{\sqrt{MS_E}}{S_X}. \]
- Resposta media para un valor de $X$ dado: \[ \mu_{Y\mid X=x}=\hat{Y} \pm t_{n-2,\,\alpha/2}\,\sqrt{MS_E}\sqrt{\frac{1}{n}+\frac{(x-\overline{x})^2}{s_X^2}}. \]
- Intervalo de predicción da resposta individual para un valor de $X$ dado: \[ \hat{Y} \pm t_{n-2,\,\alpha/2}\sqrt{MS_E}\,\sqrt{1+\frac{1}{n}+\frac{(x-\overline{x})^2}{s_X^2}}. \]