| |
1.4 A partir do producto escalar pódense medir o ángulo entre dous vectores, mediante a fórmula
<x,y> = ||x||.||y||.cos(x,y),
e a distancia entre dous puntos.
Definición.- Chamamos distancia euclidiana entre dous puntos x e y de Rp, e a denotamos por d(x,y), á norma de x–y,
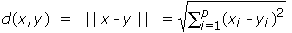
onde x = (x1,... ,xp) e y = (y1,...,yp). |
A seguinte proposición enuncia as propiedades características da distancia. A terceira é coñecida como desigualdade triangular, é consecuencia da desigualdade de Minkowski.
Proposición.- A distancia euclidiana ten as seguintes propiedades:
d(x,y)≥ 0, e d(x,y) = 0 sse x=y |
| d(x,y) = d(y,x) |
| d(x,z)≤ d(x,y)+d(y,z) |
|