| |
3.7
Definición.- Sexan X e Y espazos. Unha aplicación f: X→Y dise secuencialmente continua nun punto x0 de X se para cada sucesión {xn} en X converxente a x0, a sucesión imaxe, {f(xn)}, converxe a f(x0).
A aplicación dise secuencialmente continua se é secuencialmente continua en todos os puntos do seu dominio. |
Esta forma de continuidade denomínase continuidade secuencial. No noso contexto é equivalente á continuidade. Pódese expresar brevemente dicindo que límites e aplicacións continuas conmutan,
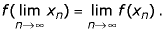
Teorema.- Sexan X e Y espazos. Unha aplicación f: X→Y é secuencialmente continua nun punto x0 sse é continua no punto.
|
|
|
3 Continuidade
3.1 Funcións continuas
3.2 Continuidade uniforme
3.3 Composición de funcións continuas
3.4 Continuidade global
3.5 Cobertura
3.6 Función combinada
3.7 Continuidade secuencial
3.8 Restricción de funcións
3.9 Conxuntos densos
3.10 Extensión de funcións
3.11 Homeomorfismos
|